Обобщенная модель стоимости опционов

Я давно обещал выложить в сеть свою статью из журнала FO с обобщенной моделью стоимости опционов, что сейчас и делаю
Сначала некоторые замечания к статье, ниже она сама
 
 
 
Обобщенная модель (ОМ) создавалась как упрощенная версия классической модели Блэка-Шолеса (БШ) для автоматической торговли опционами. Впоследствии оказалось, что главное достоинство ОМ состоит в том, что она позволяет обойтись без введения в рассмотрение понятия кривой волатильности (IV) и от всех последующих неприятностей, связанных с необходимостью ее анализа и прогнозирования.
 
Основная идея ОМ продемонстрирована на рисунке (Рис.1). Ожидаемая подвижность m ATM опционов, связанная с ценой формулой (6), есть линейная функция цены Fбазового актива (БА).

 
 
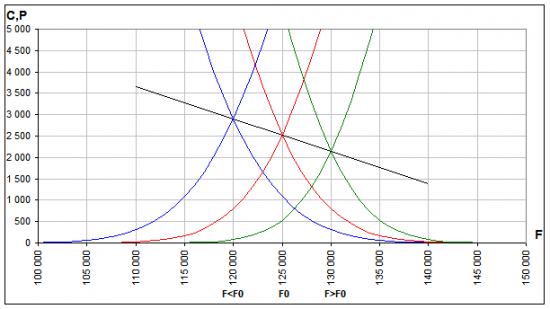
Замечание 1. Обобщенная модель не накладывает никаких ограничений на m(F), которая в силу линейности может уйти как в бесконечность, так и в область отрицательных значений. Следует понимать, что ОМ корректно описывает поведение опционов только в окрестности текущей цены БА.
Поэтому:
— не следует применять ОМ для анализа сценариев, предусматривающих значительные (в десятки процентов) изменения цены БА.
— нужно аккуратно применять ОМ в случаях, когда цена БА находится в окрестности исторического максимума (минимума). Это сейчас происходит с SP500. Увеличение цены БА приводит к меньшим, чем предписано моделью, изменениям подвижности (падать ниже некуда)
 
Замечание 2. Рыночные цены опционов с дальними страйками могут оказаться выше теоретических цен, рассчитанных по ОМ.
Проблему можно снять двумя способами:
— Ввести поправку на стоимость гарантийного обеспечения – в правую часть уравнения (3) добавить слагаемое GO*r
— Не обращать на это внимание и просто не торговать на «хвостах» — на последней НОК я пытался объяснить, что торговля такими опционами в большинстве случаев оказывается убыточной как для покупателя, так и для продавца.
 
Замечание 3. Расчетные формулы (4,5) используются только для расчета стоимости опционов “вне денег”,  при этом для расчета Call берется коэффициент bc, для Put – bp,  Стоимость опционов “в деньгах” находится по правилу паритета стоимости опционов.
То есть все, что лежит справа от цены БА, рассчитываем, подставляя в расчетные формулы коэффициент bc,  для всего, что слева – bp. Это относится и к расчету производных (greeks). Может оказаться, что при переходе цены БА через страйк, производные поменяются скачком (при bc < > bp), это плохо, особенно для дельты. Чтобы избежать скачка, необходимо предусмотреть процедуру сглаживания.
 
 
 
 
Опционы. Новый взгляд
27. сентября 2010 15:08
 
Опубликованная в 1973 году формула Блэка-Шоулза сыграла революционную роль в становлении и развитии рынка опционов. До сегодняшнего дня она и ее модификации, разработанные для опционов на различные базовые активы, входят в классический набор инструментов большинства опционных трейдеров.
Введение
Возникшие когда-то проблемы, связанные с тем, что классические формулы плохо описывали реальные рынки, были остроумно решены введением понятия ожидаемой волатильности опциона (IV, Implied Volatility) — значением параметра волатильности, которое необходимо подставить в классическую формулу с тем, чтобы ее расчетное значение совпало с рыночной ценой. По сути, IV — это поправочный коэффициент, вычисляемый для каждой цены исполнения и призванный устранить любое расхождение между расчетной и рыночной ценами опциона.
Далее было предложено аппроксимировать совокупность коэффициентов, рассчитанных для всех цен исполнения, гладкой кривой, названной кривой ожидаемой волатильности (улыбкой волатильности). Выбор конкретного вида аппроксимирующей функции достаточно произволен. Обычно это полином 5 или 6 степени, хотя на российском срочном рынке FORTS для этих целей используется комбинация из перевернутой гауссовой кривой и кривой арктангенса. В любом случае для хорошей аппроксимации необходимо 5-7 свободных параметров. Понятно, что чем больше параметров использовано, тем точнее можно провести  кривую   через любой набор точек. Однако для целей торговли необходимо не столько описать существующую волатильность рынка,   сколько предсказать ее дальнейшее поведение. Ведь именно этим показателем торгуют опционные трейдеры.
Здесь возникает проблема. Свободные параметры, используемые только в целях подгонки, не несут в себе никакого содержательного смысла. Предсказать их дальнейшее поведение и, следовательно, будущую эволюцию кривой волатильности практически невозможно.
В настоящей статье предлагается новый подход к расчету справедливой стоимости опционов. Полученные формулы, названные обобщенными, с одной стороны, охватывают более широкий класс моделей ценообразования базового актива и потому включают в себя классические  формулы  как частные случаи. С другой стороны, на практике они проще и понятнее классических формул, поскольку позволяют отказаться от использования     многопараметрической кривой ожидаемой волатильности для описания рынка. Взамен в рассмотрение вводятся только два дополнительных параметра, определяющие кривизну кривых Call и Put опционов. Полученные обобщенные формулы применимы ко всем опционным рынкам. Они значительно упрощают анализ и прогноз изменений цен опционов.
1. Уравнение баланса
Пусть изменение цены базового актива описывается стохастическим дифференциальным уравнением вида:

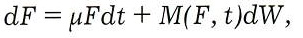
где F — стоимость базового актива, м — его доходность, t — время, W — стандартный винеровский процесс.
Назовем величину M(F, t) подвижностью (mobility) базового актива. Ее размерность совпадает с размерностью самого актива. По смыслу понятие подвижности близко к понятию волатильности, однако ее использование более предпочтительно для нас по причинам, которые будут изложены ниже. Сразу отметим, что, положив M(F,t) = oF, мы получим модель геометрического броуновского движения, использованную при выводе формулы Блэка-Шоулза.
Для определенности далее по тексту мы будем говорить только об опционах на фьючерс европейского типа.
Итак, пусть C(F, t) — справедливая цена европейского Call-опциона на фьючерс с ценой F. Сформируем безрисковый портфель, состоящий из купленного Call и фьючерсов, проданных в количестве dС/dF штук.
Стоимость такого портфеля составит

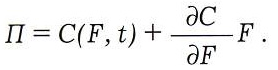
Используем лемму Ито для записи полного приращения стоимости портфеля

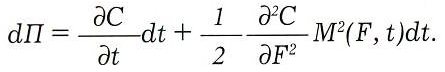
Приравняем приращение стоимости портфеля к приращению стоимости безрискового актива

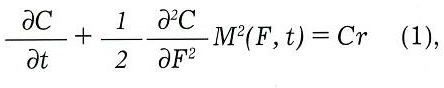
где г — ставка процента без риска.
Назовем (1) уравнением баланса.
 
2. Обобщенные формулы стоимости
Здесь мы сделаем основное предположение, представив подвижность линейной функцией цены вида:
M(F, t) = a + bF   (2),
где а, b — некоторые заданные константы.
Пока это не более чем предположение, основанное на простых наблюдениях за рынком. О том, насколько оно обоснованно, мы сможем судить позднее, когда появится возможность сравнить полученные расчетные цены с рыночными котировками опционов.
Уравнение баланса (1) принимает вид:

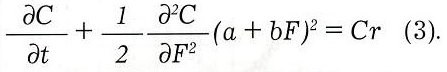
Решим уравнение (3) с краевым условием

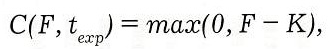
представляющим цену Call на момент его исполнения, где К — цена исполнения (Strike) опциона, t — дата исполнения (Expiration date).
В полученном решении для упрощения его вида заменим переменную а на га формальной подстановкой а = m — bF.

В итоге получим:

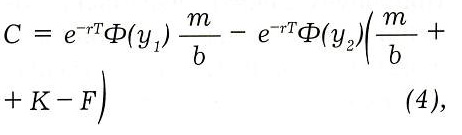
где



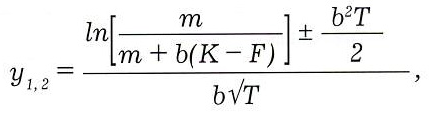
Т = texp — t — время до исполнения опциона, Ф() — интегральная функция нормального распределения.
Назовем m ожидаемой подвижностью ATM опционов (Implied Mobility), b — ожидаемым дрейфом подвижности (Implied Mobility drift). Стоимость Put получим из условия паритета стоимости опционов

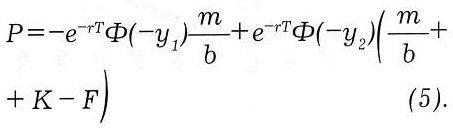
Область определения С, Р ограничена условием m + b(K — F) > 0. Это ограничение не является существенным, поскольку не удовлетворяющие ему цены исполнения К находятся далеко вне зоны торгуемых опционов.
Напомним, что процентную ставку безрискового вложения г следует учитывать только для опционов классического типа, предусматривающих перечисление премии продавцу опциона с возможностью ее размещения на безрисковый депозит. Для маржируемых опционов перечисления премии не предусмотрено. В этом случае следует положить r = 0.
Убедимся в том, что полученные формулы действительно являются обобщением классических формул стоимости опционов.
Положив подвижность соответствующей модели геометрического броуновского движения M(F,t) = oF = а + bF и подставив найденные из этого условия га = = oF, b = о в формулу (4), мы получим знакомую формулу Блэка для Call-опциона на фьючерс.

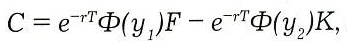
где

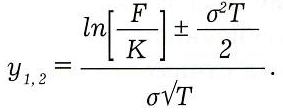
Из модели броуновского движения следует т = о, b = 0. Предельным переходом при b -> 0 получим формулу Башелье (r = 0).

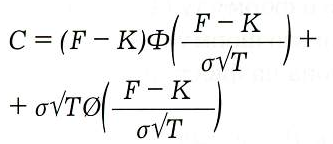
Не утомляя читателя выкладками, отметим, что все частные производные («greeks») для обобщенных формул рассчитываются аналитически.

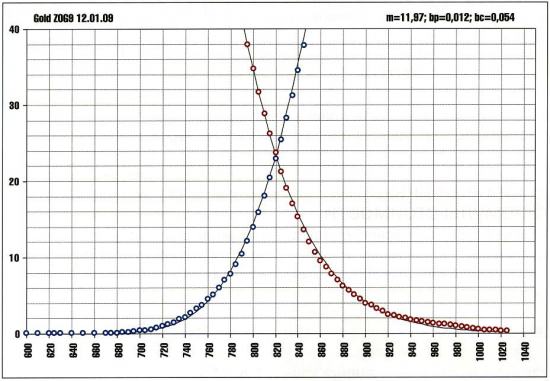
Рис. 1 Аппроксимация цен закрытия февральских опционов на золото

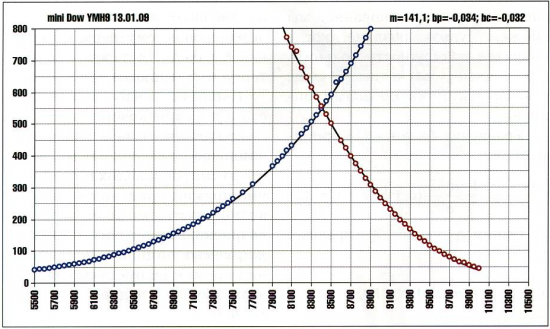
Рис. 2 Аппроксимация цен закрытия мартовских опционов на индекс Dow Jones
 
3. Использование обобщенных формул для описания рынков
Попробуем понять, насколько хорошо полученные обобщенные формулы описывают реальные опционные рынки. С этой целью
применим их для аппроксимации официальных цен закрытия контрактов, торгующихся на западных биржах (на российских биржах понятия цены закрытия опционов не существует).
Ожидаемую подвижность ATM (at the money) опционов для подстановки в формулы (4),(5) найдем из соотношения

которое получается из (4) или (5) при К = F, b -> 0. Здесь С0 — высота точки пересечения кривых Call и Put. Подбор коэффициентов дрейфа b С, b Р проведем отдельно для кривых Call и Put по методу наименьших квадратов.
На рисунках 1 и 2 приведены результаты аппроксимации очень разных по сути опционов на золото (NYSE LIFFE Gold) и биржевой индекс (CBOT mini Dow). В обоих случаях разность между ценами, полученными при помощи обобщенных формул, и ценами закрытия минимальна. Аналогичные результаты получаются и для других рынков.
Таким образом, можно утверждать, что трех параметров т, b с, b р первый из которых определяет высоту точки пересечения кривых Call и Put, а два других — степень их кривизны, оказывается вполне достаточно для описания опционных рынков без дополнительной подгонки. Меньшим количеством параметров в общем случае обойтись нельзя (подобно тому, как для описания треугольника нужно знать, например, две стороны и угол между ними). Большего же числа, как показывает практика, не требуется. Все это позволяет утверждать, что полученные обобщенные формулы практически универсальны.
 
4. Подвижность рынка
Рассмотрим подробнее, что представляет собой введенная выше подвижность M(F, t) и чем, по мнению автора, она удобнее волатильности при описании рынка.
Для произвольного интервала времени Т посчитаем статистическую оценку подвижности базового актива

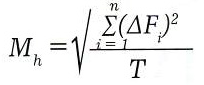
Здесь n — количество изменений цены актива на интервале Т, а Fi — изменение цены на i-м шаге.
Оценку Мh, посчитанную на интервале 1 торговый день, назовем исторической дневной подвижностью базового актива. В отличие от исторической волатильности, которая рассчитывается на произвольном интервале времени, дневная подвижность является характеристикой торгового для, отражающей интенсивность торгов.
На рисунке 3 приведены сравнительные графики исторической дневной подвижности фьючерса на индекс РТС (Mh) и ожидаемой подвижности трехмесячных опционов на индекс РТС (т), посчитанной по формуле (6), в период с 21.12.07 по 11.12.08.
Ожидаемая подвижность т, а следовательно, и стоимость ATM опционов оказывается величиной вполне предсказуемой. Простейший из прогнозов формулируется так: ожидаемая подвижность изменяется в сторону исторической дневной подвижности, которую, в свою очередь, можно непрерывно измерять в реальном времени. Заметим, что аналогичный прогноз, сформулированный для волатильности, гораздо менее достоверен. В хорошей предсказуемости, по мнению автора, первое из преимуществ подвижности.
Далее, подставляя прогнозируемое значение Mh в уравнение баланса (1), составленное для портфеля, мы получаем соотношение, позволяющее предсказать финансовый результат торгового дня:

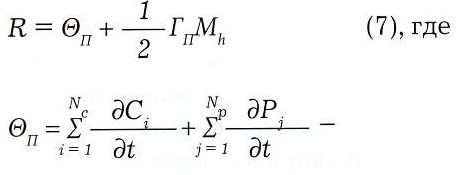
суммарная тета портфеля,

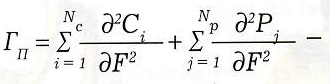
суммарная гамма.

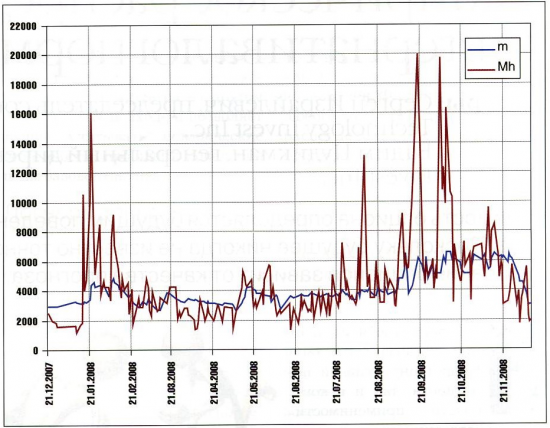
Рис. 3 Графики дневной подвижности фьючерса на индекс РТС и ожидаемой подвижности трехмесячных опционов на индекс РТС

Первое слагаемое в (7) показывает, как за день изменится суммарная стоимость составляющих портфель опционов. Второе слагаемое отражает финансовый результат, который будет получен от торговли базовым активом в процессе непрерывного дельта-хеджирования опционного портфеля (мы не рассматриваем здесь торговлю опционами без хеджирования, считая это занятие несерьезным).
Заключение
В настоящей работе предложен новый подход к расчету справедливой стоимости опционов. Он основан на введении в рассмотрение понятия подвижности базового актива, удобной и вполне предсказуемой характеристики активности рынка. Предположение о линейной зависимости, существующей между подвижностью и стоимостью базового актива, приводит к обобщенным формулам, эффективному инструменту анализа и прогноза стоимости опционов.
Единственный недостаток, возникающий при отказе от привычной кривой ожидаемой волатильности, связан с возможностью сравнительного анализа цен опционов по виду этой кривой. Недостаток легко снимается введением в рассмотрение понятия ожидаемой подвижности опциона — значения М, которое нужно подставить в уравнение баланса (1) для конкретного опциона с тем, чтобы превратить его в тождество. Совокупность таких значений образует гладкую кривую — аналог кривой ожидаемой волатильности.
Таким образом, три интуитивно понятных параметра т, Ьс, Ьр позволяют полностью описать любые опционные рынки. Поведение параметров хорошо предсказуемо во времени, что позволяет прогнозировать поведение рынка опционов в целом.