Блог им. student_vrt
Параметрическое оптимальное f при нормальном распределении: Разбор 3 главы книги Ральфа Винса “Математика управления капиталом”
- 07 февраля 2018, 13:41
- |

Продолжение краткого изложения книги Ральфа Винса “Математика управления капиталом” с комментариями DTI.
Сегодня разбираем третью главу “Параметрическое оптимальное f при нормальном распределении”. В ней рассматриваются различные виды распределений вероятности и методы их анализа. Также описывается нахождение оптимального f при условии нормального распределения.
Виды распределений
Существуют различные непрерывные и дискретные распределения. Дискретные распределения являются “ячеистыми”, что уменьшает информационное содержание распределения. Однако и на практике приходится жертвовать частью информации, сохраняя при этом профиль распределения.
#важно Сделать непрерывное распределение дискретным можно путем создания ячеек. Однако дискретное распределение превратить в непрерывное невозможно
Непрерывное распределение является серией бесконечно малых ячеек:
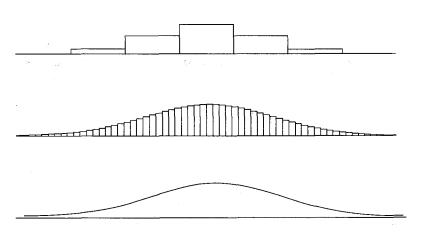
Величины, описывающие распределения
Центральная тенденция
Первое, что необходимо знать о группе данных, или первый момент распределения, — его центральное значение. Для его оценки используют различные показатели, наиболее распространенным из которых является среднее арифметическое значение.
Среднее арифметическое — сумма значений, соответствующих точкам распределения, деленная на их количество. Формула:

#важно Среднее арифметическое обычно оказывается плохим выбором, если распределение имеет широкие хвосты, то есть если вероятность получить значение, удаленное от среднего, высока. В такой ситуации средние, рассчитанные по разным наборам случайно выбранных из распределения точек, будут сильно различаться
Могут использоваться также другие спецификации среднего: геометрическое (для положительных значений), гармоническое или квадратическое (среднеквадратический корень). Формулы:

Средние значения всегда подчиняются следующим соотношениям: арифметическое всегда больше или равно геометрическому, а геометрическое больше или равно гармоническому.
Существуют альтернативные показатели центральной тенденции.
Медиана — значение, находящееся посередине расположенного по возрастанию ряда данных. Медиана делит распределение надвое так, чтобы площадь под кривой функции плотности вероятности одной части была равна площади под кривой второй части. В отличие от среднего арифметического величина медианы не искажается крайними случайными значениями.
Мода — наиболее часто повторяющееся значение данных. Данный показатель отражает пик кривой распределения. В некоторых распределениях нет моды, а в других их несколько. Мода никак не зависит от крайних случайных значений, и ее можно рассчитать быстрее, чем среднее арифметическое или медиану.
Распределение также можно разделить
- тремя квартилями, чтобы получить четыре области равного размера или вероятности;
- девятью децилями, чтобы получить десять областей равного размера или вероятности;
- 99 перцентилями, чтобы получить сто областей — при этом 50 перцентиль является медианой, а вместе с 25 и 75 перцентилями — квартилем;
- N–1 квантилем, чтобы получить N областей.
Разброс значений
Второй момент распределения — это изменчивость данных, или “ширина” относительно центрального значения. Она измеряет разброс распределения относительно первого момента. Чаще всего в качестве оценки разброса используют дисперсию и стандартное отклонение. Также может применяться среднее отклонение.
Среднее абсолютное отклонение, или просто среднее отклонение, — среднее арифметическое абсолютных отклонений значения каждой точки от среднего арифметического всех значений. Иными словами, это среднее удаление от среднего. Формула:

#важно Данная формула позволяет вычислить среднее абсолютное отклонение по всей совокупности данных. Однако его можно рассчитать и по выборке из них. Для этого в формуле необходимо заменить 1/N на 1/(N-1)
Дисперсия — среднее арифметическое квадратов абсолютных отклонений значения каждой точки от среднего арифметического всех значений. Иными словами, это средний квадрат удаления от среднего. Формула:

Стандартное отклонение (сигма, σ) — квадратный корень из дисперсии.
#важно Формулу для дисперсии — а соответственно, и для стандартного отклонения, также можно применять для совокупности данных или для выборки из них. Второй вариант также требует замены 1/N на 1/(N-1)
Асимметрия и эксцесс
Третий момент распределения — асимметрия, описывающая асимметричность распределения относительно среднего значения. В отличие от первых двух моментов является безразмерной — это просто число, показывающее скос распределения. Положительная асимметрия означает, что хвосты толще с правой стороны распределения, и наоборот. Совершенно симметричное распределение имеет нулевой скос.
Различные виды асимметрии:
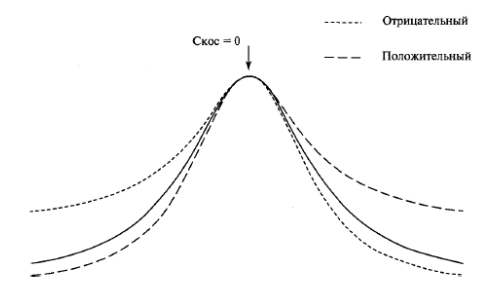
В симметричном распределении среднее, медиана и мода имеют одинаковое значение. В ином случае верно следующее равенство: Среднее–Мода = 3(Среднее–Медиана).
Среднее, мода и медиана при асимметричном распределении:
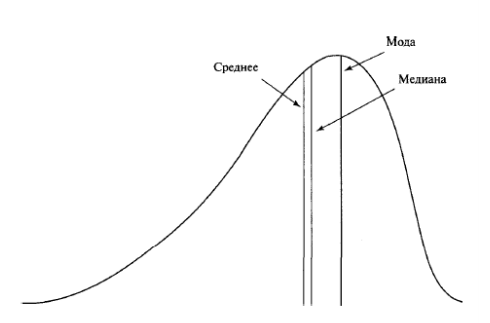
Есть много способов для расчета асимметрии, и они часто дают различные ответы. Два распространенных варианта:

Четвертый момент распределения — эксцесс. Он показывает, насколько у распределения плоско- или островершинная форма по сравнению с нормальным. Как и асимметрия, это безразмерная величина.
Менее остроконечная, чем нормальная, кривая имеет эксцесс отрицательный, и наоборот. Для вершины, аналогичной пику нормального распределения, эксцесс равен нулю — в таком случае он называется нормальным.
Различные виды эксцесса:
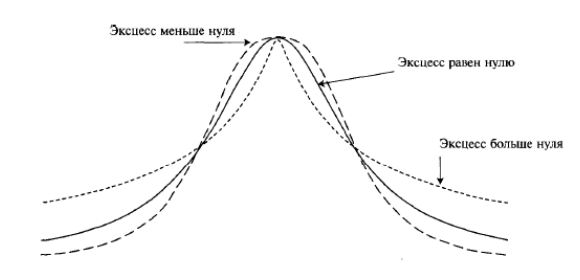
Наиболее распространенные методы расчета эксцесса:

Примеры распределений
Нормальное
Нормальное распределение (также называется распределением Гаусса или Муавра) считается наиболее ценным, поскольку моделирует многие явления. Также оно является предельной формой некоторых других типов распределений, например, Пуассона и Стьюдента (t-распределения). Иными словами, при достаточно большом количестве точек (N) эти распределения похожи на нормальное.
Продолжение читайте в Блоге DTIтеги блога Александр Бутманов
- Amazon
- Apple
- bitcoin
- Brent
- DTI
- ETF
- ICO
- interactive brokers
- IPO
- RTSI
- Telegram
- TON
- Uber
- VIX
- акции
- банки
- бизнес
- биткоин
- блокчейн
- Брокер
- брокерский счет
- бутманов
- Валюта
- Валюты
- ВДеталях
- волатильность
- втб
- газпром
- гособлигации США
- деньги
- доллар
- Доллар рубль
- Дорофеев
- Евро
- ЕС
- Золото
- Инвестидеи
- Инвестидея
- инвестиции
- инвестиционная идея
- Индия
- искусственный интеллект
- Китай
- ключевыетемы2018
- ключевыетренды2019
- Кризис
- криптовалюта
- Криптовалюты
- крипторынок
- криптосфера
- Курсы
- лукойл
- Медицина
- мнение по рынку
- налоги
- недвижимость
- нефть
- Новости
- Облигации
- Образование
- опек+
- оффтоп
- политика
- Пошлины
- прогнгоз
- прогноз
- прогнозы
- рбк
- Регулирование
- рецессия
- ритейл
- Россия
- Рубль
- русал
- рынок
- санкции
- сбербанк
- Сервисы
- СМИ
- ставки
- Стартапы
- США
- Технобудущее
- технологии
- токены
- торговля
- Торговые войны
- Трамп
- трейдинг
- тренды
- философия
- Финансы
- финтех
- Фондовый рынок
- фрс
- Фьючерсы
- ЦБ РФ
- Экономика
- юмор



















Это в теории. А на практике очень даже.