Блог им. Zmey56
Использование метода Монте-Карло для создания портфеля
- 26 апреля 2020, 14:17
- |
Начинающие (да и не только) инвесторы часто задаются вопросом о том, как отобрать для себя идеальное соотношение активов входящих в портфель. Часто (или не очень, но знаю про двух точно) у некоторых брокеров эту функцию выполняет торговый робот. Но заложенные в них алгоритмы не раскрываются.
В этом посте будет рассмотрено то, как оптимизировать портфель при помощи Python и симуляции Монте Карло. Под оптимизацией портфеля понимается такое соотношение весов, которое будет удовлетворять одному из условий:
- Портфель с минимальным уровнем риском при желаемой доходности;
- Портфель с максимальной доходностью при установленном риске;
- Портфель с максимальным значением доходности
Для расчета возьмем девять акций, которые рекомендовал торговый робот одного из брокеров на начало января 2020 года и так же он устанавливал по ним оптимальные веса в портфеле: 'ATVI','BA','CNP','CMA', 'STZ','GPN','MPC','NEM' и 'PKI'. Для анализа будет взяты данные по акциям за последние три года.
#Загружаем библиотеки import pandas as pd import yfinance as yf import numpy as np import matplotlib.pyplot as plt # Получаем данные по акциям ticker = ['ATVI','BA','CNP','CMA', 'STZ','GPN','MPC','NEM', 'PKI'] stock = yf.download(ticker,'2017-01-01', '2019-01-31') <a name="cut"></a> <br /><br />
Если сложить долю всех акций, входящих в портфель, то сумма должна стремиться к единице (а лучше быть равна). Дальше как обычно проведем подготовку данных для расчетов:
# Выделение скорректированой цены закрытия all_adj_close = stock[['Adj Close']] # ежедневная доходность all_returns = all_adj_close.pct_change() # узнаем среднюю доходность и получаем ковариационную матрицу mean_returns = all_returns.mean() cov_matrix = all_returns.cov()Теперь можно провести расчет для весов предложенных торговым роботом и узнать доходность данного портфеля за последник три года и стандартное отклонение.
#предложение по весам торгового робота robot = np.array([0.0441, 0.1030, 0.1086, 0.2070, 0.1525, 0.0714, 0.0647, 0.1828, 0.0661]) # доходность, стандартное отклонение и коэффициент Шарпо portfolio_return_robot = np.sum(mean_returns * robot) portfolio_std_dev_robot = np.sqrt(np.dot(robot.T,np.dot(cov_matrix, robot))) sharpo_robot = portfolio_return_robot/portfolio_std_dev_robot # объединим полученные значения в таблицу и выведем ее robot_result = np.array([portfolio_return_robot, portfolio_std_dev_robot, sharpo_robot]) robot_result = np.array([portfolio_return_robot, portfolio_std_dev_robot, sharpo_robot]) robot_result = np.concatenate((robot_result, robot), axis=0) robot_sim_result = pd.DataFrame(robot_result, columns=['Robot'], index=['ret','stdev','sharpe',ticker[0],ticker[1],ticker[2],ticker[3],ticker[4],ticker[5],ticker[6],ticker[7],ticker[8]]) print(robot_sim_result)
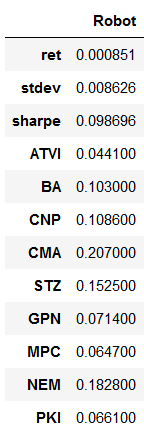
Симуляция Монте-Карло
Первоначально небольшое вступительное слово о том, как используется метод Монте-Карлоя для оптимизации портфеля
Сначала акциям задаются случайные веса, после чего производится расчет доходности и стандартного отклонения. Полученные значения сохраняются. Следующим шагом случайным образом меняются веса (главное не забывать, что их сумма должна составлять единицу) и все повторяется — расчет и сохранение полученного значения. Количество итераций зависит от времени, мощностей компьютера для расчета и рисков, который готов принять инвестор. В этот раз попробуем провести 10000 расчетов для выявления портфеля с минимальным убытком и максимальным значением коэффициента Шарпа.
#создаем массив из нулей
num_iterations = 10000
simulation_res = np.zeros((4+len(ticker)-1,num_iterations))
# сам итерации
for i in range(num_iterations):
#Выбрать случайные веса и нормализовать, чтоб сумма равнялась 1
weights = np.array(np.random.random(9))
weights /= np.sum(weights)
#Вычислить доходность и стандартное отклонение
portfolio_return = np.sum(mean_returns * weights)
portfolio_std_dev = np.sqrt(np.dot(weights.T,np.dot(cov_matrix, weights)))
#Сохранить все полученные значения в массив
simulation_res[0,i] = portfolio_return
simulation_res[1,i] = portfolio_std_dev
#Вычислить коэффициент Шарпа и сохранить
simulation_res[2,i] = simulation_res[0,i] / simulation_res[1,i]
#Сохранить веса
for j in range(len(weights)):
simulation_res[j+3,i] = weights[j]
# сохраняем полученный массив в DataFrame для построения данных и анализа.
sim_frame = pd.DataFrame(simulation_res.T,columns=['ret','stdev','sharpe',ticker[0],ticker[1],ticker[2],ticker[3],ticker[4],ticker[5],ticker[6],ticker[7],ticker[8]])Теперь можно рассчитать портфель с максимальным коэффициентом Шарпа или минимальным риском.# узнать максимальный Sharpe Ratio
max_sharpe = sim_frame.iloc[sim_frame['sharpe'].idxmax()]
# узнать минимальное стандартное отклонение
min_std = sim_frame.iloc[sim_frame['stdev'].idxmin()]
print ("The portfolio for max Sharpe Ratio:\n", max_sharpe)
print ("The portfolio for min risk:\n", min_std)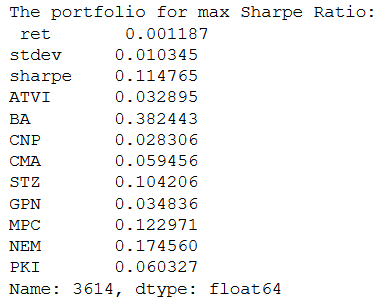
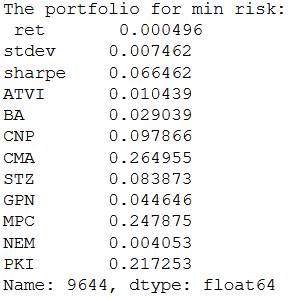
Самое конечно интересное в этих данных(как и в любых других), что их можно визуализировать:
fig, ax = plt.subplots(figsize=(10, 10))
#Create a scatter plot coloured by various Sharpe Ratios with standard deviation on the x-axis and returns on the y-axis
plt.scatter(sim_frame.stdev,sim_frame.ret,c=sim_frame.sharpe,cmap='RdYlBu')
plt.xlabel('Standard Deviation')
plt.ylabel('Returns')
plt.ylim(0,.0015)
plt.xlim(0.007,0.012)
#Plot a red star to highlight position of the portfolio with highest Sharpe Ratio
plt.scatter(max_sharpe[1],max_sharpe[0],marker=(5,1,0),color='r',s=600)
#Plot a blue star to highlight position of the portfolio with minimum Variance
plt.scatter(min_std[1],min_std[0],marker=(5,1,0),color='b',s=600)
#Plot a green star to highlight position of the portfolio with minimum Variance
plt.scatter(portfolio_std_dev_robot, portfolio_return_robot,marker=(5,1,0),color='g',s=600)
plt.show()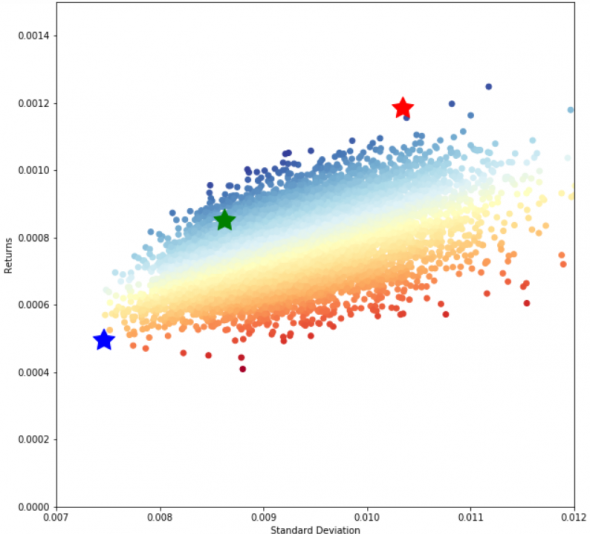
Портфель с максимальным коэффициентом Шарпа показан красной звездой, синей — с минимальным стандартным отклонением и зеленой — предложенный роботом.Как видно — портфель предложенный роботом не совпадает с этими показателями, но на каком остановиться портфеле — выбор остается за инвестором. А я постраюсь в конце года вернуться к сравнению портфелей. А сейчас все три портфеля находятся в просадке.



















только из HFT :)
Сам метод оценки акций я не понял?
Если это -
Портфель с минимальным уровнем риском при желаемой доходности;
Портфель с максимальной доходностью при установленном риске;
Портфель с максимальным значением доходности
То это черный ящик, где кто-то что то посчитал. А потом с этими данными уже работаем.
Монте-Карло здесь привязан за уши. Проще искать экстремум многомерной функции. Благо в питоне всякие методы есть.
Но экстремум и искать не нужно. В результате получите больший вес у быстрее росшей прошлом акции. Не факт, что это правильно.
Ковариации тоже не айс, но они более устойчивы