Тренд (Trend)
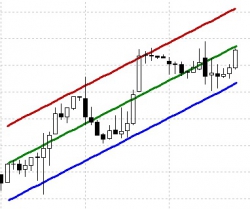
Тренд (от англ. Trend-«тенденция») — долговременная тенденция изменения исследуемого временного ряда. В техническом анализе подразумевается направленность движения цен или значений индексов.
Методы оценки
Параметрические — рассматривают временной ряд как гладкую функцию от t: X(t)=f(t),t=1...n;. При этом сначала выявляют один либо несколько допустимых типов функций f(t); затем различными методами (например, МНК) оценивают параметры этих функций, после чего на основе проверки критериев адекватности выбирают окончательную модель тренда. Важное значение для практических приложений имеют линеаризованные тренды, то есть тренды, приводимые к линейному виду относительно параметров использованием тех или иных алгебраических преобразований.
Непараметрические — это разные методы сглаживания исходного временного ряда — скользящие средние (простая, взвешенная), экспоненциальное сглаживание. Эти методы применяются как для оценки тренда, так и для прогнозирования. Они полезны в случае, когда для оценки тренда не удается подобрать подходящую функцию.
Модели трендов:
Линейный - y=a+b×t
Экспоненциальный - y=a+b^t
Гиперболический - y=a+b⁄t
Степенной - y=a+t^b
Полиноминальный - y=a+b×t+c×t^2+⋯z×t^n

Логарифмический - y=a+b×log(t)

Логистический - y=1/(e^(a+b×t)+1)
Методы оценки[править | править вики-текст]Параметрические — рассматривают временной ряд как гладкую функцию от t: {\displaystyle X(t)=f(t),t=1...n;} X(t)=f(t),t=1...n;. При этом сначала выявляют один либо несколько допустимых типов функций {\displaystyle f(t)} f(t); затем различными методами (например, МНК) оценивают параметры этих функций, после чего на основе проверки критериев адекватности выбирают окончательную модель тренда. Важное значение для практических приложений имеют линеаризованные тренды, то есть тренды, приводимые к линейному виду относительно параметров использованием тех или иных алгебраических преобразований.Непараметрические — это разные методы сглаживания исходного временного ряда — скользящие средние (простая, взвешенная), экспоненциальное сглаживание. Эти методы применяются как для оценки тренда, так и для прогнозирования. Они полезны в случае, когда для оценки тренда не удается подобрать подходящую функцию.Методы оценки[править | править вики-текст]
Методы оценки
Параметрические — рассматривают временной ряд как гладкую функцию от t: X(t)=f(t),t=1...n;. При этом сначала выявляют один либо несколько допустимых типов функций f(t); затем различными методами (например, МНК) оценивают параметры этих функций, после чего на основе проверки критериев адекватности выбирают окончательную модель тренда. Важное значение для практических приложений имеют линеаризованные тренды, то есть тренды, приводимые к линейному виду относительно параметров использованием тех или иных алгебраических преобразований.
Непараметрические — это разные методы сглаживания исходного временного ряда — скользящие средние (простая, взвешенная), экспоненциальное сглаживание. Эти методы применяются как для оценки тренда, так и для прогнозирования. Они полезны в случае, когда для оценки тренда не удается подобрать подходящую функцию.
Модели трендов:
Линейный - y=a+b×t

Экспоненциальный - y=a+b^t
Гиперболический - y=a+b⁄t
Степенной - y=a+t^b
Полиноминальный - y=a+b×t+c×t^2+⋯z×t^n

Логарифмический - y=a+b×log(t)

Логистический - y=1/(e^(a+b×t)+1)

Методы оценки[править | править вики-текст]Параметрические — рассматривают временной ряд как гладкую функцию от t: {\displaystyle X(t)=f(t),t=1...n;} X(t)=f(t),t=1...n;. При этом сначала выявляют один либо несколько допустимых типов функций {\displaystyle f(t)} f(t); затем различными методами (например, МНК) оценивают параметры этих функций, после чего на основе проверки критериев адекватности выбирают окончательную модель тренда. Важное значение для практических приложений имеют линеаризованные тренды, то есть тренды, приводимые к линейному виду относительно параметров использованием тех или иных алгебраических преобразований.Непараметрические — это разные методы сглаживания исходного временного ряда — скользящие средние (простая, взвешенная), экспоненциальное сглаживание. Эти методы применяются как для оценки тренда, так и для прогнозирования. Они полезны в случае, когда для оценки тренда не удается подобрать подходящую функцию.Методы оценки[править | править вики-текст]
- Параметрические — рассматривают временной ряд как гладкую функцию от t: {\displaystyle X(t)=f(t),t=1...n;}
. При этом сначала выявляют один либо несколько допустимых типов функций {\displaystyle f(t)}
; затем различными методами (например, МНК) оценивают параметры этих функций, после чего на основе проверки критериев адекватности выбирают окончательную модель тренда. Важное значение для практических приложений имеют линеаризованные тренды, то есть тренды, приводимые к линейному виду относительно параметров использованием тех или иных алгебраических преобразований.
- Непараметрические — это разные методы сглаживания исходного временного ряда — скользящие средние (простая, взвешенная), экспоненциальное сглаживание. Эти методы применяются как для оценки тренда, так и для прогнозирования. Они полезны в случае, когда для оценки тренда не удается подобрать подходящую функцию.


















