Дюрация и риск процентных ставок

Дюрация, пожалуй, одно из самых неудачно интерпретируемых понятий в российском сегменте аналитики инструментов фиксированного дохода. Большинство отечественных финансовых интернет-ресурсов пытаются рассказать о ней “простыми словами” Вот наиболее часто встречающиеся определения:

Дюрация облигации — это эффективный срок до погашения облигации… С помощью дюрации инвесторы и аналитики измеряют средний срок возврата инвестиций

Дюрация облигации — некоторый промежуток времени, период до момента полного возврата капиталов, вложенных в приобретение этой ценной бумаги

Дюрация — это срок, в течение которого необходимо держать облигацию, чтобы полностью вернуть изначальные инвестиции.

Дюрация Маколея — это тип измерения дюрации, который оценивает, сколько дней (лет) потребуется инвестору, чтобы вернуть инвестиции в облигацию за счет общих денежных потоков по ней

Дюрация показывает среднее время, за которое мы полностью вернем свои вложения в облигации

Дюрация — это средняя окупаемость инвестиции

Если говорить простым языком, это период окупаемости вложенных средств в облигацию.

Дюрация определяет какое число дней или лет требуется для инвестирования в долговой актив. 

Помимо “срока полной окупаемости” и “среднего времени возврата инвестиций” дюрацию часто рассматривают как “средневзвешенный срок до погашения облигации”, “точку равновесия всех дисконтированных платежей” и приблизительную меру процентного риска облигации.

Забегая вперед, отметим, что для практических целей нужно использовать последнее определение:

Дюрация — мера чувствительности цены облигации к изменению процентной ставки.

Все так называемые “простые” объяснения слишком расплывчаты либо неточны, и могут лишь еще больше запутать читателя. Представление о дюрации как о «промежутке времени с момента покупки облигации до момента полного возврата затрат на приобретение этой ценной бумаги» является ошибочным.

Дюрация Маколея

Понятие “длительность” (duration) в качестве “сущности временной составляющей займа” ввел канадский экономист Фредерик Маколей; он впервые использовал его в своей монографии “Some Theoretical Problems Suggested by the Movements of Interest Rates, Bond Yields and Stock Prices in the United States since 1856”, опубликованной в начале 1938 г.

Маколей обратил внимание, что флуктуации цен облигаций возрастают с увеличением срока до погашения. Он объяснил это тем, что далеко не все инвесторы в длинные бумаги собираются удерживать их долгое время. Но на коротком горизонте трудно составить прогноз доходности за период владения. Многое зависит от мнения рынка о будущих процентных ставках, степени уверенности в надежности выплат и, кроме того, невозможно принудить потенциального покупателя к совершению сделки по нужной продавцу цене. В силу этого длинные облигации менее ликвидны.

С другой стороны, Маколей задался вопросом: каким образом можно сравнивать “продолжительность” займов? Для займов с единственным будущим платежом, выданных под одну и ту же процентную ставку, это просто — короче тот из них, который имеет меньший срок погашения. Но если платежи распределены во времени, а ставки дисконтирования различны, задача усложняется. Желательно иметь соответствующую метрику, которую он и предложил называть “дюрацией” Согласно его подходу, займы тогда будут по существу различаться по продолжительности, когда они имеют разные дюрации.

Срок погашения — самый неподходящий вариант для использования в качестве такой метрики. Он просто соответствует последней выплате, которая может быть незначительной частью общего денежного потока. Так происходит, например, в случае равномерно уменьшающихся платежей для аннуитета определенного вида. При сравнении облигаций необходимо также учитывать ставку купона и доходность к погашению (yield) Ведь бумага, которая при прочих равных условиях выплачивает более высокий купон, находится в обращении, по сути, менее продолжительное время.

Маколей предположил, что дюрация любого займа, включающего более одного будущего платежа, должна быть чем-то вроде средневзвешенного значения сроков погашения его отдельных частей. Взвешивать платежи можно двумя способами — по их абсолютной величине или по приведенной стоимости. Первый способ Маколей счел недопустимым, так как он приводит к абсурдно большим показателям дюрации.

Например, “дюрация” портфеля из двух бескупонных облигаций, полученная при взвешивании их номиналов, рассчитывается как (1000∙T₁ + 1000∙T₂)/2000. Если первая из бумаг погашается через год, а вторая через 100 лет, такая “дюрация” будет равна 50.5 лет. Но при эффективной ставке, допустим, в 5% цена первой облигации составляет 952.4 ед., а второй — 7.6 ед. Получается, что вторая облигация стоимостью менее 1% всего портфеля вносит практически равный вклад в его “продолжительность” Зато дюрация, рассчитанная на основе приведенных стоимостей (цен облигаций), будет меньше одного года, что выглядит вполне разумным.

В результате Маколей предложил следующее правило вычисления дюрации:

• Дюрация облигации равна средневзвешенному значению дюраций отдельных платежей (купонов и номинала)
• Дюрация каждого единичного платежа равна времени, оставшемуся до его поступления, а вес — отношению приведенной стоимости платежа к общей сумме всех приведенных стоимостей, т.е. к цене облигации.

Единица измерения дюрации — промежуток времени, т.е. число лет или дней. В своей монографии Маколей приводит ее формулу в предположении плоской кривой доходности (единой ставки дисконтирования всех денежных потоков) и периодическом начислении процентов, а также исследует некоторые свойства этой метрики. Перечислим их вкратце:

1. Дюрация облигации всегда меньше либо равна сроку до ее погашения. Она совпадает со сроком погашения, если облигация не выплачивает купонов.
2. При прочих равных условиях, чем выше ставка купона и доходность к погашению, тем меньше дюрация.
3. Если облигация торгуется не ниже номинала, ее дюрация монотонно растет с увеличением срока до погашения, асимптотически приближаясь к предельному значению 1+ 1/ i, где i — доходность к погашению, приходящаяся на один период.
4. Если облигация торгуется с дисконтом, т.е. когда ставка купона меньше доходности к погашению, дюрация имеет локальный максимум, а затем плавно снижается к предельному значению 1+ 1/ i.

В качестве иллюстрации этих свойств ниже построен анимированный график зависимости дюрации Маколея от срока до погашения облигации при ставках купона 1%, 5%, 10% и 15%, и изменяющейся от 5% до 15% требуемой ставки дисконтирования. Для простоты расчетов использовано непрерывное начисление процентов и ставки купона (последнее можно наглядно представить, как ежедневную выплату купона)

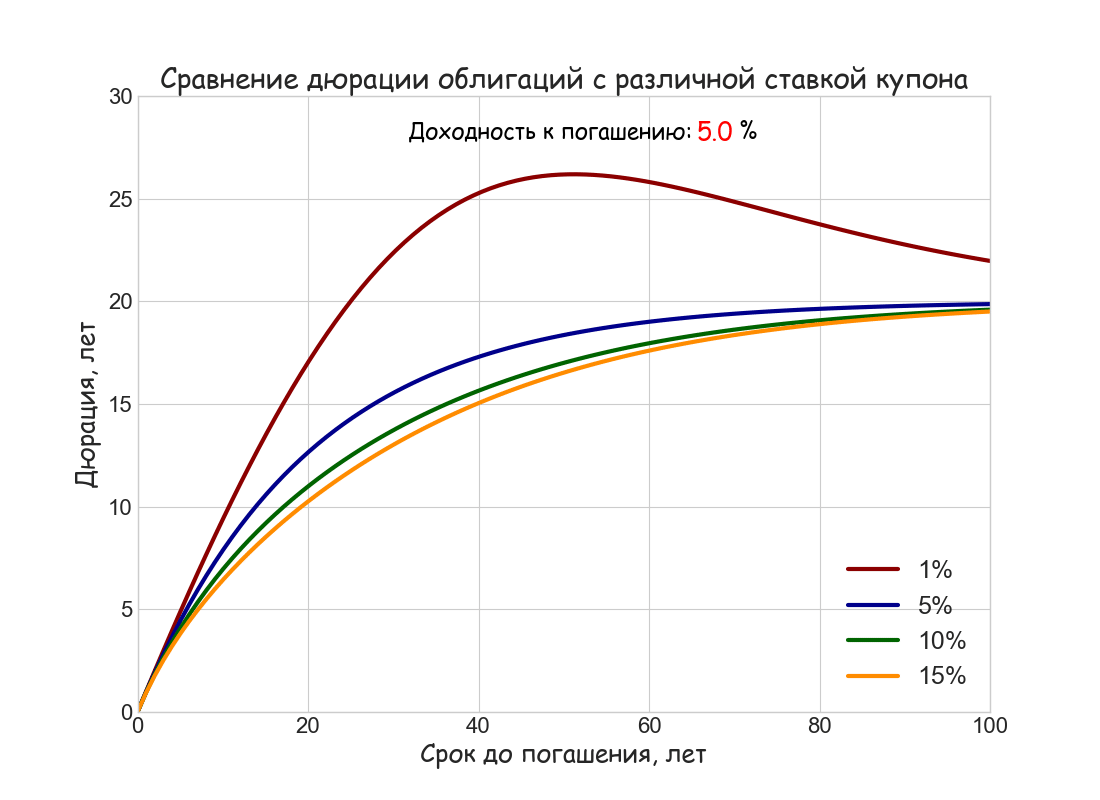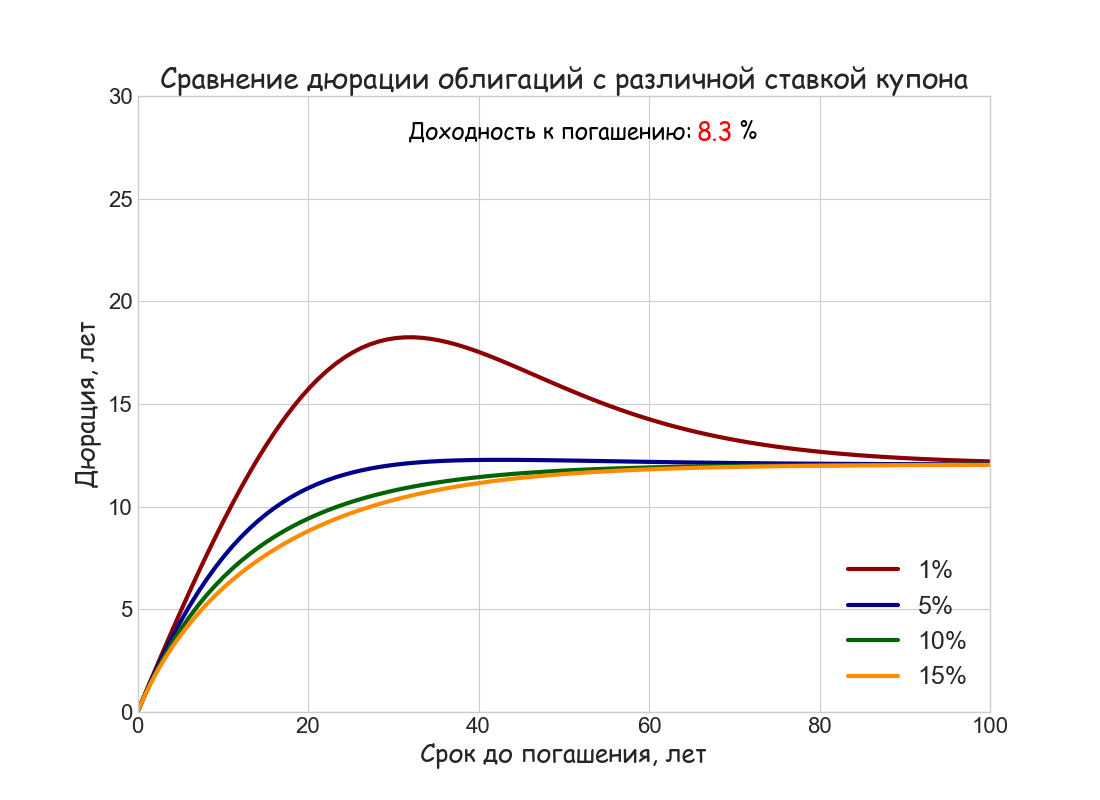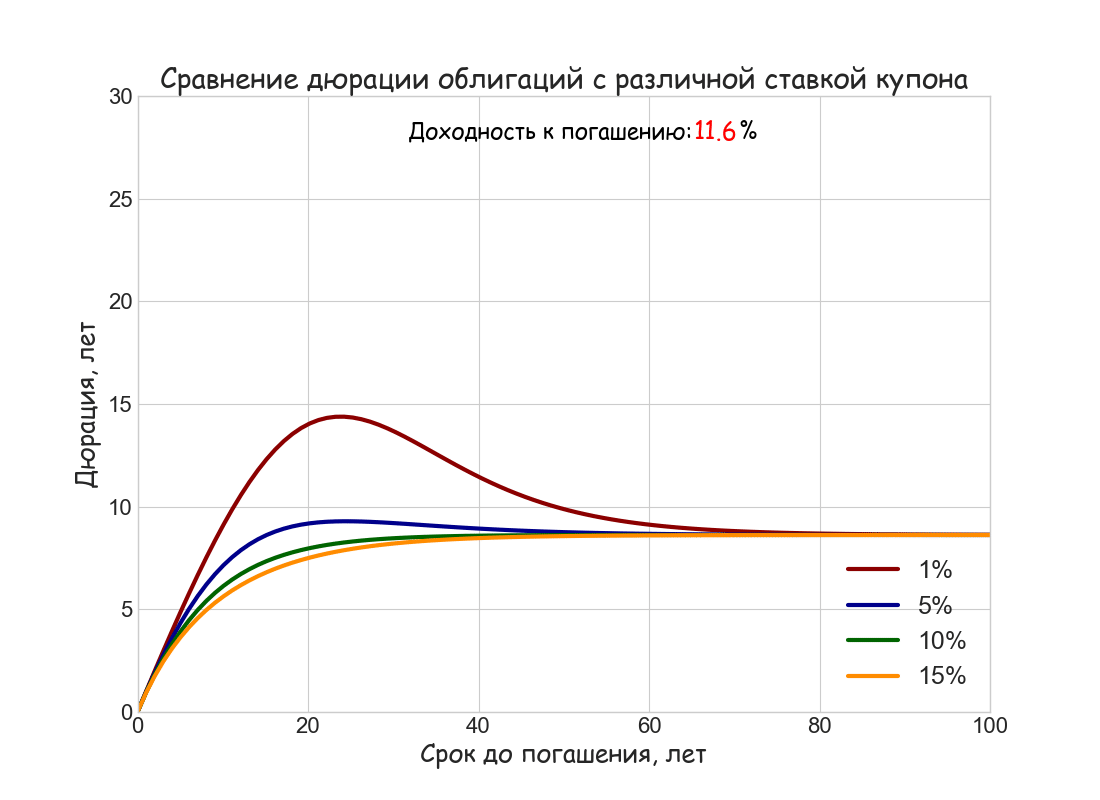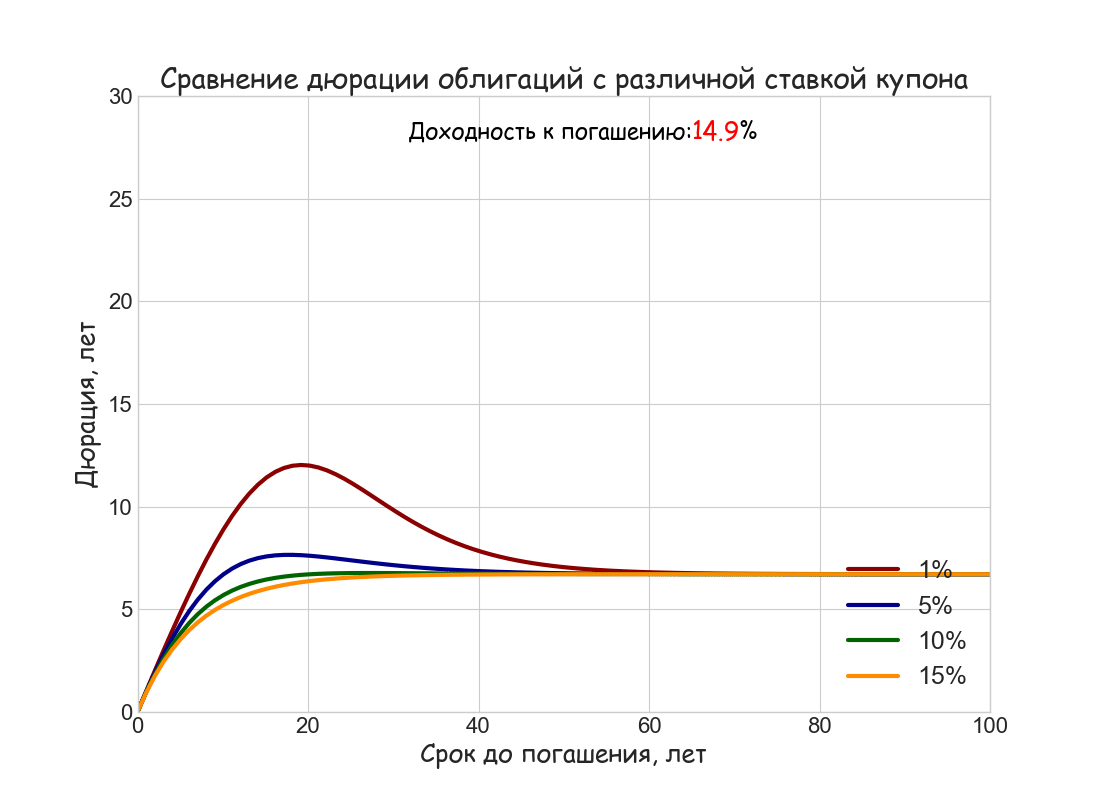
Маколей обратил внимание, что новая метрика в какой-то степени может объяснить поведение цен облигаций на разных временных горизонтах. Если флуктуации доходности за период владения у коротких и длинных бумаг различаются существенно, то для сверхдлинных — 50-летних и 100-летних — они примерно равны. Это хорошо согласуется с ограниченностью величины дюрации при больших сроках до погашения.

Кроме того, он указал на недостатки упрощенного варианта формулы, подразумевающей плоскую кривую доходности. В реальности будущие денежные потоки дисконтируются по различным ставкам, поэтому следует использовать выражение для дюрации в самом общем виде. Возможна ситуация, когда у двух торгующихся в разные даты облигаций равны номиналы, сроки до погашения, ставки купона и доходности к погашению, — а, следовательно, и цены, — но они будут иметь разные дюрации. Так может произойти, если первая облигация торгуется в условиях инвертированной кривой доходности, а вторая — нормальной.

В заключение отметим, что Маколей не использовал выражения “средний срок до погашения”, “эффективный срок до погашения” и т.д. Их, конечно, нельзя признать ошибочными, ведь они ничего толком не определяют и слишком расплывчаты. Но в них нет и никакой особой необходимости. Дюрацию Маколея лучше воспринимать именно так, как ее ввел сам Маколей (метод расчета и формула), а если уж и применять в качестве «меры продолжительности», то только для сравнения денежных потоков.

Почему дюрация это не срок окупаемости?

Трудно сказать, откуда в отечественной финансовой журналистике взялось отождествление дюрации и срока возврата инвестиций. Да и что, собственно, под этим подразумевают сами авторы? Если взять любое пособие по корпоративным финансам и посмотреть там, что такое “срок окупаемости” проекта или вложений, то обнаружится, что речь идет о другом.

Срок окупаемости — это количество периодов (обычно измеряемых в годах), необходимых для того, чтобы сумма ожидаемых денежных потоков по проекту равнялась его первоначальным затратам. Другими словами, срок окупаемости — это время, за которое фирма восстанавливает свои первоначальные инвестиции. Существует также подход, учитывающий дисконтирование, — т.н. экономический срок окупаемости. В этом случае суммируются не сами ожидаемые платежи, а их приведенные стоимости.

В отличие от дюрации платежи, поступающие после срока окупаемости, не влияют на его величину. Допустим, мы нашли, что срок окупаемости проекта при данной ставке дисконтирования равен 6-ти годам. Если мы добавим к текущему графику дополнительные платежи в 7-м, 8-м и т. д. годах, срок окупаемости останется прежним. Но дюрация проекта увеличится — в ее расчете участвуют все денежные потоки. Даже этот простой пример противоречит пониманию дюрации как срока окупаемости, не говоря уже о том, что две эти величины численно не совпадают.

По-видимому, в своем понимании дюрации наши авторы опираются на некоторые англоязычные ресурсы (Инвестопедию и другие): “it is the weighted average number of years that an investor must maintain a position in the bond until the present value of the bond’s cash flows equals the amount paid for the bond.” “the Macaulay duration measures, in years, the amount of time required for an investor to be repaid his initial investment in a bond” Но там написана, откровенно говоря, какая-то нелепость. Ведь приведенная стоимость будущих денежных потоков по облигации как раз и равна ее цене, т.е. уплаченным за облигацию деньгам. 

Между тем обычная англоязычная Википедия и все более-менее серьезные источники подобных толкований дюрации Маколея не содержат. Фраза в Википедии “weighted average time until cash flows are received” — это краткое изложение правила вычисления дюрации. Маколей в своей монографии также нигде не упоминал окупаемость либо возврат изначальных вложений.

Возможно, идея «окупаемости» зародилась в смежной области — математике страхования. В начале 20-го века актуарии рассматривали проблему определения так называемого “эквивалентного срока” (equated time) для ряда выплат, поступающих в разное время. В симметричном решении, предполагающем единую ставку дисконтирования, весь денежный поток заменяется бескупонной облигацией с той же приведенной стоимостью и таким сроком погашения, при котором ее номинал будет равен общей сумме платежей.

“Эквивалентный срок” можно сопоставить с периодом окупаемости в том смысле, что на этом горизонте накопленная стоимость инвестиции становится равна общей сумме всех обещанных денежных потоков. Но равен ли он дюрации?

Рассмотрим следующий пример

Численный пример 1. Пятилетняя облигация торгуется за номинал и выплачивает ежегодный купон по ставке 15% годовых. Чему равны ее дюрация Маколея и “эквивалентный срок”?

Дюрацию Маколея можно найти с помощью формулы Excel ДЛИТ(дата_согл; дата_вступл_в_силу; купон; доход; частота;[базис]) В ней нельзя напрямую указать срок погашения облигации, и приходится подбирать даты:

D = ДЛИТ(«1/1/2023»;«1/1/2028»;15%;15%;1) = 3.855 лет

По условию цена облигации равна номиналу, т.е. 1000 руб. Доходность совпадает со ставкой купона. Размер ежегодного купона равен 150 руб, общая сумма предстоящих выплат за пять лет —1750 руб. Поэтому, чтобы найти эквивалентный срок необходимо решить уравнение относительно T:

1000∙(1+15%)ᵀ = 1000 + 5∙1000∙15% = 1750;

T = ln(1.75)/ln(1.15) = 4 года.

Полученные в примере величины дюрации Маколея и “эквивалентного срока” различаются, хоть и незначительно. Чем меньше доходность, ставка купона и срок до погашения тем ближе друг к другу эти две метрики. Для бескупонной облигации они будут равны, в остальных случаях “эквивалентный срок” всегда превосходит дюрацию. В качестве наглядной иллюстрации отличия метрик, они совместно построены на анимированном графике ниже:

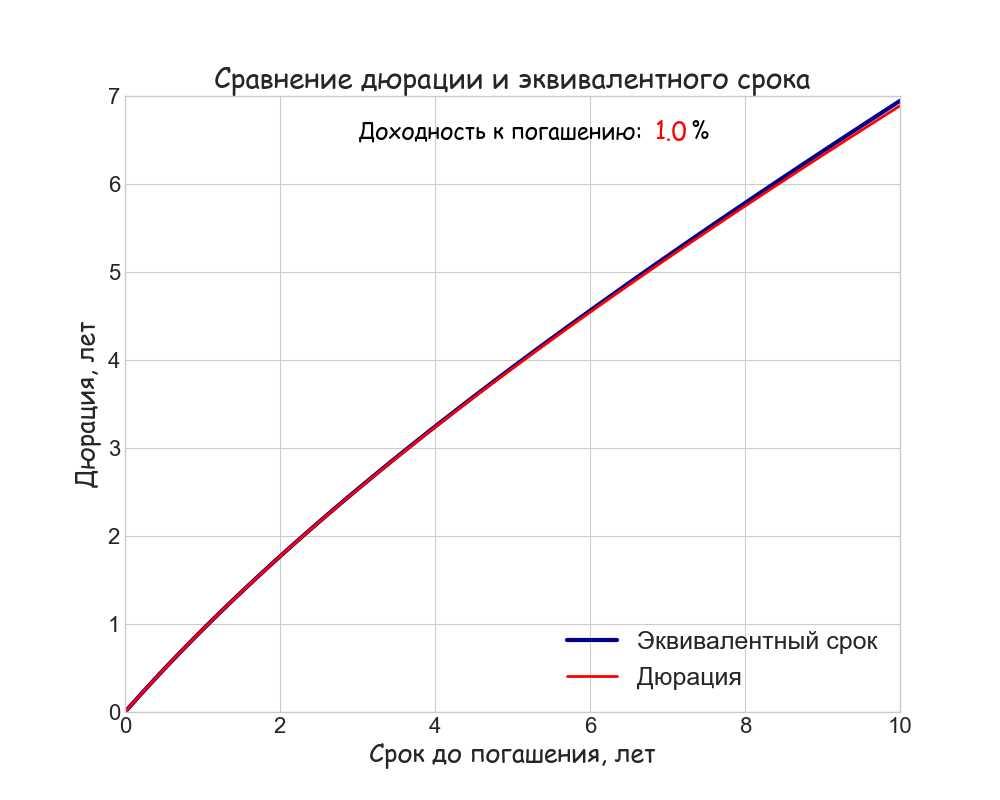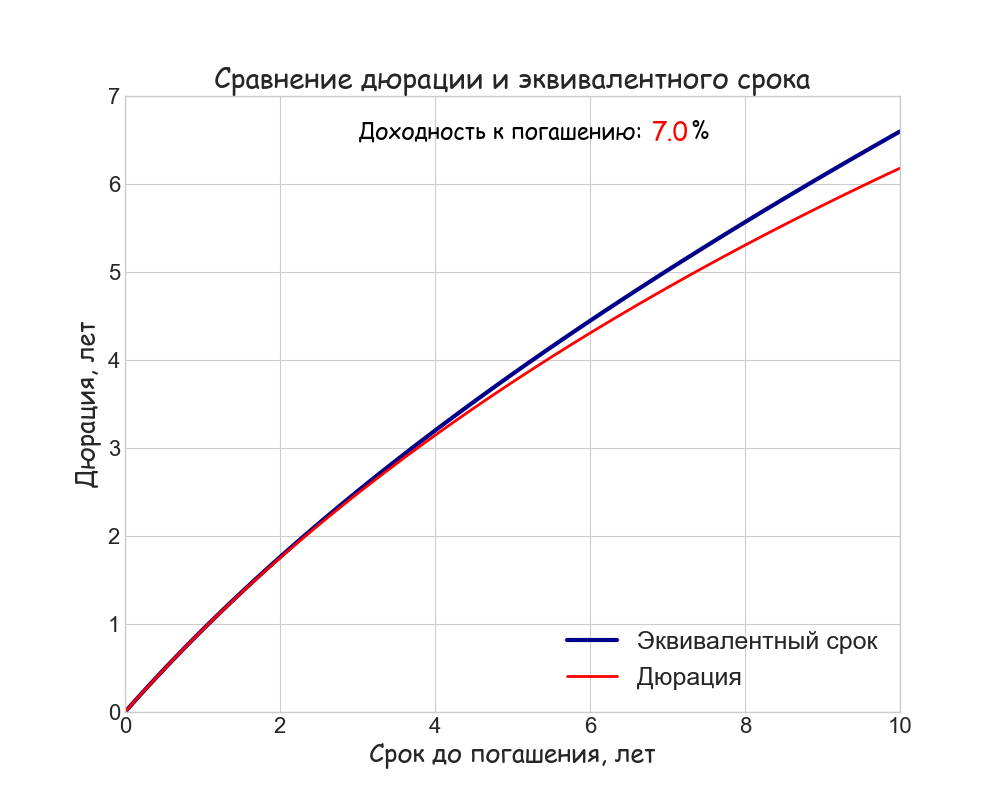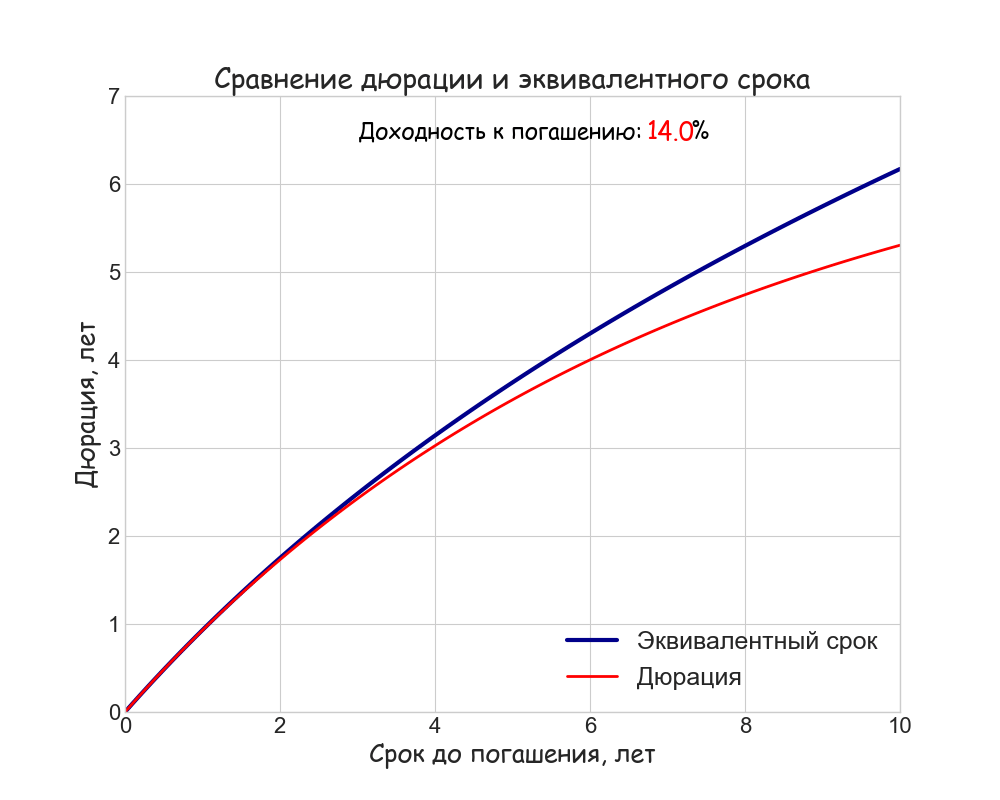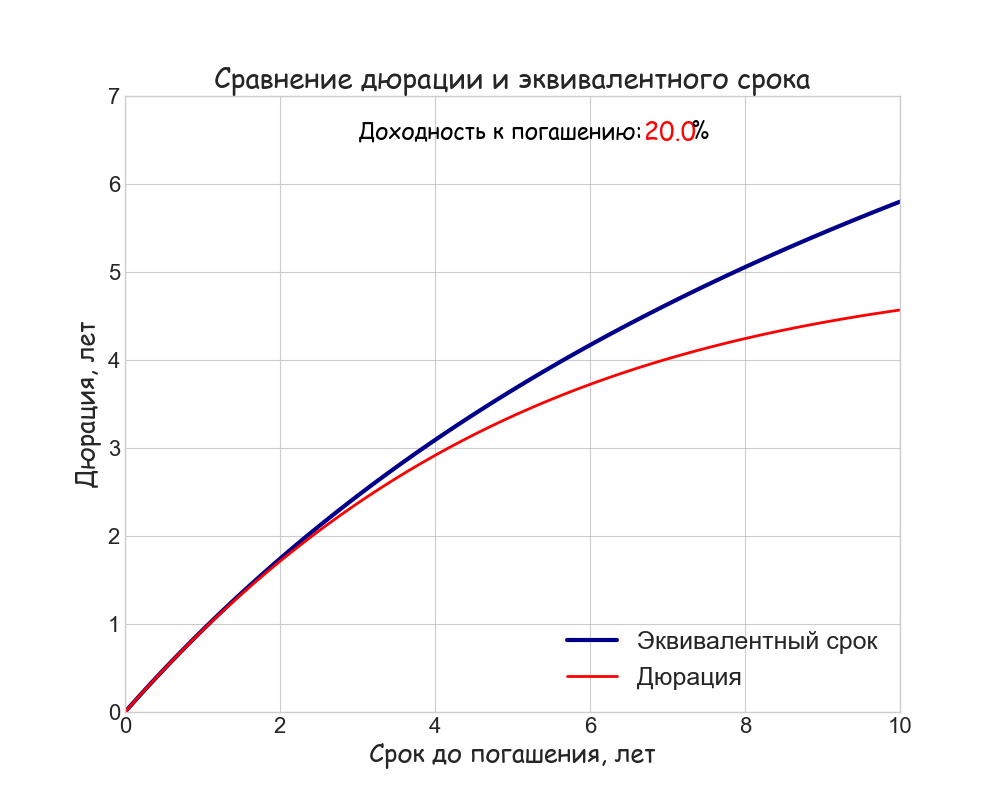
Для упрощения расчетов мы, как и в прошлый раз, использовали непрерывное начисление процентов; ставка купона равна 15%. Видно, что расхождение будет минимальным при не слишком высоких значениях доходности и на коротком горизонте. Скорее всего, именно этот факт и послужил когда-то основанием считать дюрацию “сроком окупаемости” И тем не менее, это разные понятия. Эквивалентный срок будет неограниченно расти с увеличением срока до погашения, а дюрация купонной облигации не превосходит некоторой предельной величины.

Таким образом, если бы в перечисленных в самом начале объяснениях дюрации «простыми словами»

1) корректно излагалось, что понимается под сроком окупаемости

2) указывалось на их приближенный характер и границы применимости

вопросов у читателей было бы куда меньше.

Впрочем, даже уточненное определение вряд ли поможет на практике. Ведь что такое окупаемость в понимании обычного человека? Это возврат вложенных средств плюс заработанный процент. Допустим, ставки по всем облигациям одинаковы и не меняются со временем (плоская и статичная кривая доходности) Тогда стоимость инвестиции будет плавно расти, т.е. она будет “окупаться” в любой момент времени, и не обязательно дожидаться какого-то определенного срока. С другой стороны, внезапный рост ставок через время близкое к дюрации может привести к тому, что накопленная стоимость портфеля в этот момент окажется немногим больше вложенной суммы. Особенно это актуально для длинных облигаций. Да, концепция эквивалентного срока обладает математической элегантностью, но реальная жизнь зачастую преподносит сюрпризы. Утверждать, например, как сделано в этой статье: “Получается, что деньги, которые инвестор вложил в ОФЗ 26218, вернутся на три года раньше, чем облигация будет погашена” — значит, вводить читателя в заблуждение.

Таким образом, представление о дюрации как  о “сроке возврата инвестированной стоимости”,  является неверным.

Дюрация — мера чувствительности цены облигации к изменению процентных ставок

В своей монографии Маколей размышлял о связи дюрации и ценового риска. Она должна была объяснить, почему при колебаниях ставок, волатильность цен облигаций не увеличивается линейно в зависимости от срока погашения. Изменение цены облигации с сроком погашения в один год будет сильно отличаться от изменения цены облигации с сроком погашения в десять лет, и изменение цены десятилетней облигации также будет существенно отличаться от изменения сорокалетней облигации; но сорокалетние и столетние облигации будут двигаться практически вместе. Оставался лишь шаг, чтобы получить выражение, связывающее флуктуации цен и доходностей облигаций.

В 1939 году британский экономист Джон Хикс опубликовал знаменитую работу “Value and Capital”, где, в частности, вывел формулу эластичности (мера чувствительности одной переменной к изменению другой) “капитальной стоимости” денежного потока по отношению к фактору дисконтирования. Он назвал эту величину “средним периодом”, поскольку она оказалась равна средней продолжительности сроков поступления различных платежей, когда они взвешены с учетом дисконтирования.

Он также объяснил, почему эластичность — обычно безразмерная величина — измеряется в промежутках времени. Причиной этого является сложное начисление процентов. Полная ставка за два года не равна удвоенной годовой ставке, поэтому время нельзя устранить из расчетов при пропорциональных изменениях переменных. Хикс предложил использовать “средний период” в качестве инструмента для планирования производства и принятия решений по капиталовложениям в бизнесе. Судя по всему, он не был знаком с работой Маколея, иначе заметил бы, что определенная им величина полностью совпадает с дюрацией.

Позднее Лоуренс Фишер в статье “An Algorithm for Finding Exact Rates of Return” (1966) независимо показал, что дюрация Маколея имеет свойство эластичности. Он выразил процентное изменение цены облигации через изменение ее доходности и рассмотрел два случая — для ежегодного и непрерывного начисления процентов.

Легко проверить, что при годовом начислении процентов выражения Хикса и Фишера совпадают, так как Δd =Δ[1/(1+r)] = —1/(1+r)²∙Δr, т.е. это фактически замена переменной. Для новой переменной r дюрация Маколея D уже не будет эластичностью в строгом смысле, но остается мерой чувствительности цены облигации к изменению процентной ставки. Величина MD = D/(1+r) со временем получила название модифицированной дюрации. Если число периодов начисления в году составляет m, модифицированная дюрация MD = D/(1+r/m) При непрерывном начислении модифицированная дюрация и дюрация Маколея численно равны: MD = D. Поскольку именно непрерывное начисление является основным подходом в современном финансовом анализе, зачастую говорят о просто дюрации, не указывая, какая из двух имеется в виду.

Численный пример 2. Предположим, что 10-летняя облигация с купонной ставкой 10% и полугодовыми купонами торгуется за номинал. Каково будет примерное изменение ее цены, если доходность внезапно вырастет на 50 б.п.?

Рассчитаем модифицированную дюрацию облигации при полугодовом начислении процентов, используя формулу Excel:

MD = МДЛИТ(дата_согл; дата_вступл_в_силу; купон; доход; частота) = МДЛИТ(«1/1/2023»;«1/1/2033»;10%;10%;2) = 6.23

Используя соотношение ΔP/P ≈ — MD∙Δr, получим, что цена облигации упадет приблизительно на 6.23∙0.5% = 3.1%, до 96.9%. Для сравнения, корректный расчет новой цены в Excel показывает, что она станет равной 96.95%

Таким образом, дюрация дает более правильное представление о ценовом риске. При сопоставлении двух различных денежных потоков с точки зрения того, как их относительная стоимость будет реагировать на одно и то же (по величине) изменение доходности, мы руководствуемся параметром дюрации, а не сроком до погашения. Важность этого факта трудно переоценить.

Поправки и границы применимости

Точность оценки ΔP/P будет зависеть как от значения самой дюрации MD, так и от величины изменения доходности Δr. Чем больше оба этих параметра, тем хуже приближение. Дело в том, что дюрация — это линейная мера, тогда как зависимость цены облигации от процентной ставки существенно нелинейна.

В качестве примера рассмотрим 15-летнюю бескупонную облигацию с доходностью к погашению 5% и текущей ценой P₀ = 481 денежных единиц (при ежегодном начислении процентов)

Если провести касательную к графику цены в точке r = 5% (см. рисунок), то тангенс угла ее наклона будет равен — P₀∙MD. Можно сказать, что в этом заключается “геометрический” смысл дюрации. При изменении ставки на Δr приближенное значение цены, рассчитанное через модифицированную дюрацию, P₀ + ΔP𝒹, будет соответствовать точке на касательной, а корректное значение, P₀ + ΔP — точке на синей кривой. Из рисунка видно, что фактическая цена всегда получится больше, чем ее аппроксимация. Это следствие выпуклости функции P(r).

Когда Δr слишком велико, формулу для процентного изменения цены облигации следует уточнить, добавив в нее поправку — модифицированную выпуклость MС. Модифицированная выпуклость — величина второго порядка, соответствующая последующему элементу в разложении функции цены в ряд Тейлора. Она может быть выражена через модифицированную дюрацию.

В нашем примере с бескупонной облигацией MC = T∙(T + 1)/(1+r)² = 15∙16/(1+5%)² = 217.7. Если доходность, например, упадет на 2. п.п. — до 3%, то цена бумаги, рассчитанная через дюрацию, увеличится приблизительно на ΔP𝒹 = — P₀∙MD∙Δr = — 481∙15/(1+5%)∙( —2%) = 137.4 до 618.4 ден. ед. Поправка за счет выпуклости даст дополнительную прибавку 481∙0.5∙217.7∙(0.02)² = 20.9 ден. ед и уточненное значение составит 618.4 + 20.9 = 639.4. ден. ед., что немногим меньше фактической цены P(r +Δr) = P₀ + ΔP = 642 ден.ед.

Понятия дюрации и выпуклости в той форме, что они были сформулированы выше, справедливы в предположении, что

1. все выплаты по облигации известны заранее
2. ставка дисконтирования одинакова для денежных потоков различной срочности (плоская кривая доходности)

И действительно, как можно найти дюрацию Маколея, допустим, для флоатера или линкера? Суммы купонов (а у линкеров и номинальная стоимость) по этим бумагам привязаны к индикаторам, значение которых в будущем не определено. Модифицированная дюрация, как мера ценового риска, рассчитывается через доходность к погашению и ее малые изменения. Но как обсуждалось ранее, доходность к погашению — это агрегированный параметр, не отражающий временную структуру процентных ставок. Для того чтобы метод модифицированной дюрации работал, необходимо изменение доходностей всех облигаций на одну и ту же величину, а это возможно только в случае плоской кривой, т.е. при единой эффективной ставке дисконтирования денежных потоков. 

Дюрация как точка равновесия

Помимо “эффективного срока до погашения” и меры ценового риска существует интерпретация дюрации как некоего “центра тяжести”:

“Наиболее простое объяснение сути дюрации — это представление финансовых потоков как грузиков, расположенных вдоль стержня (временной оси), находящегося в равновесии на одной точке опоры. Длина стержня — срок до погашения. Дюрация — длина участка от левого края стержня до точки опоры. Расстояние между грузиками — купонный период”

“Дюрация — это точка опоры, уравновешивающая все дисконтированные платежи по облигации”

Эти дисконтированные платежи схематично указаны столбиками в примере на рисунке ниже; “вес” каждого последующего купона уменьшается, последняя выплата включает номинал облигации.

Действительно, если мы изготовим гирьки с весами, равными приведенным стоимостям денежных потоков, и поместим их на линейку в соответствующем порядке, то центр масс всей системы окажется как раз в “точке дюрации” Это следует из его определения как оно вводится в любом школьном учебнике по физике. Точка на оси абсцисс, соответствующая центру масс невесомого продольного стержня с грузиками:

x꜀ = Σ mₖ·xₖ/M , где mₖ — массы грузиков, xₖ — их координаты, М = Σ mₖ — общая масса системы.

В определении дюрации Маколея весам соответствуют приведенные стоимости денежных потоков Cₖ — PV(Cₖ), координатам — сроки до погашения Tₖ, общей массе — стоимость портфеля облигаций.

Но что нам дает эта отсылка к курсу механики, какой новый взгляд на дюрацию? Рассчитав центр тяжести, мы знаем как обустроить качели или обеспечить поступательное движение тела. А что делать с этими “грузиками-купонами”, куда их приспособить?

Ведь можно придумать любую другую аналогию. Например, читатели, знакомые с теорией вероятностей, могут заметить, что дюрация Маколея — это математическое ожидание некоторой случайной величины, которая принимает значения, равные срокам Tₖ с вероятностями PV(Cₖ)/P₀. Выходит, что дюрация — ожидаемое в вероятностном смысле время поступления всех платежей? Эта трактовка имеет такое же право на жизнь, как и та, что связана с “центром тяжести”. Однако толку в этом никакого, ведь сроки выплат вовсе не случайны.

Для того чтобы придать обсуждаемому “равновесию” практическое содержание, мы должны вернуться к связи дюрации и процентного риска.

У инвестора в облигации могут быть различные цели. Если он собирается вскоре продать купленные бумаги, его портфель подвержен главным образом ценовому риску, который проявится в снижении стоимости облигаций в результате неожиданного повышения рыночных ставок. Приближенной мерой этого риска, как уже обсуждалось выше, выступает модифицированная дюрация MD:

ΔP/P ≈ — MD∙Δr ;

Инвестор также может удерживать облигации до погашения. В этом случае основным становится риск реинвестирования, который мы до сих пор не рассматривали. Мы предполагаем, что облигации свободны от дефолта и за время их обращения все обещанные выплаты гарантированы. Тогда общий накопленный доход FV(T) по конкретной бумаге будет складываться из суммы ее номинальной стоимости, выплаченных купонов и дохода от их реинвестирования. Если ставка остается постоянной на протяжении всего срока T, то реализованная доходность за период владения (HPR) будет равна доходности к погашению r.

Однако в реальности ставки, под которые будут реинвестированы полученные купоны, заранее неизвестны. В результате тренд на их снижение может привести к тому, что HPR окажется меньше изначально рассчитанной доходности r. В этом и состоит риск реинвестирования. Для бескупонной облигации он равен нулю, т.к. нечего реинвестировать. А в общем случае этот риск тем выше, чем больше срок до погашения и ставка купона.

Приближенной мерой волатильности накопленного дохода FV в случае непрерывного начисления процентов служит разность срока до погашения T и дюрации D: T — D (соответственно, для периодического начисления [T — D]/[1+r/m]) Она показывает, насколько в процентном отношении вырастет этот доход при увеличении ставки реинвестирования r.r. (reinvestment rate) на 100 б.п.:

ΔFV/FV ≈ (T — D)∙Δr.r.

Ниже построен анимированный график зависимости меры [T — D] от срока до погашения T при ставках купона 1%, 5%, 10% и 15%, и изменяющейся от 5% до 15% доходности к погашению; как и в примере с дюрацией Маколея использовано непрерывное начисление процентов и ставки купона.

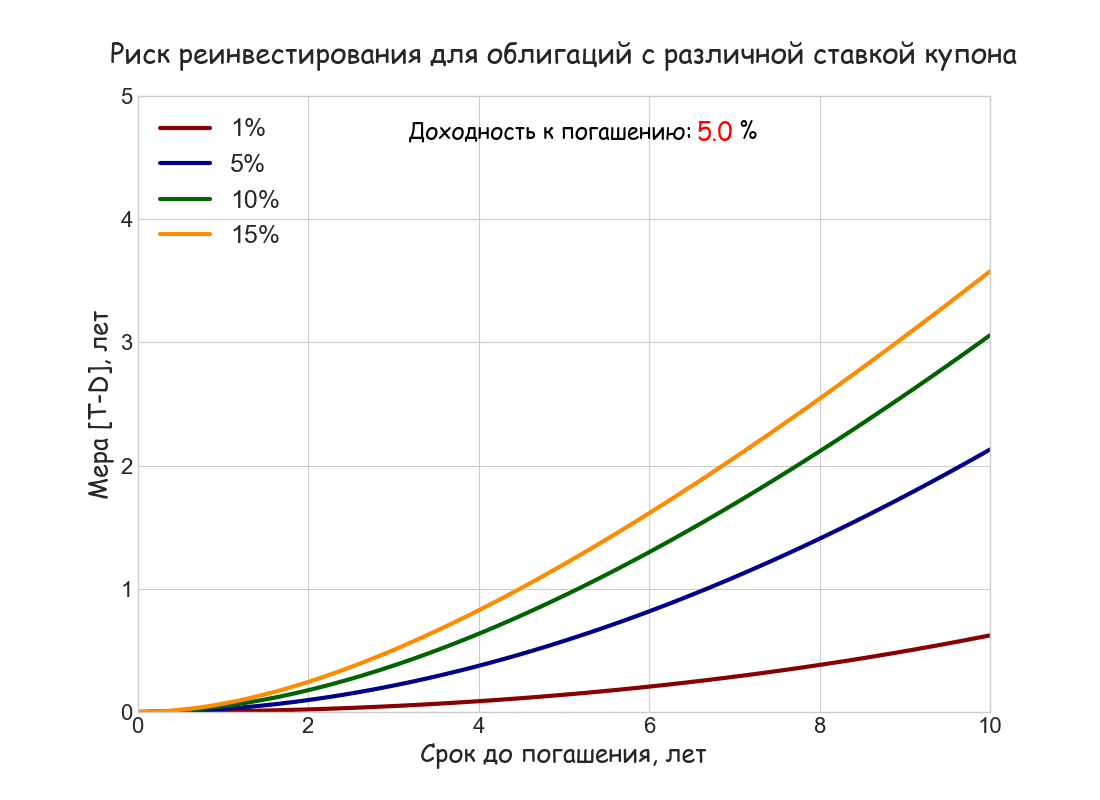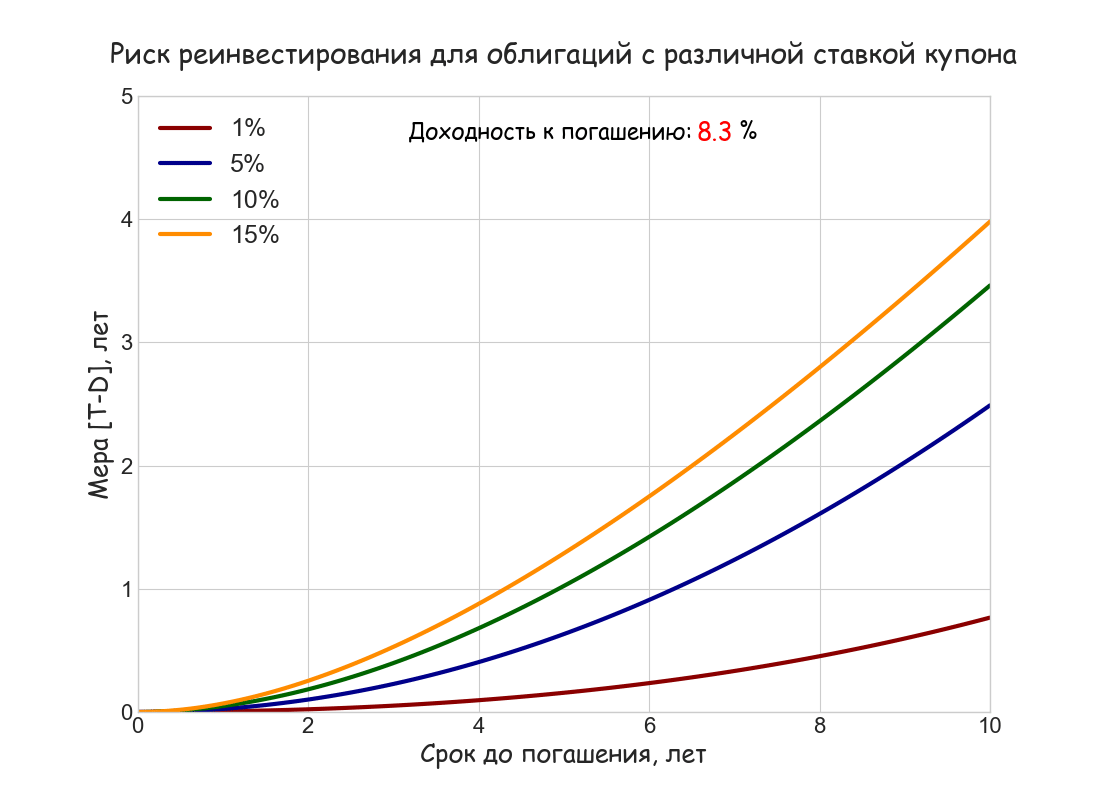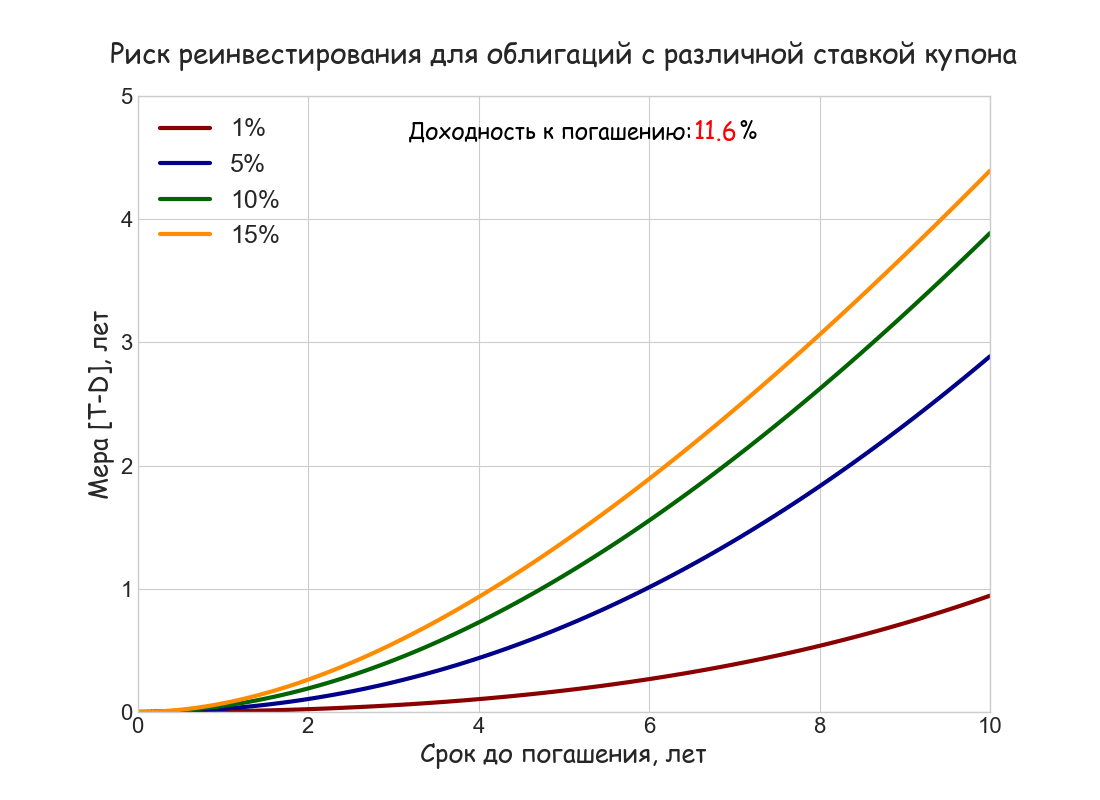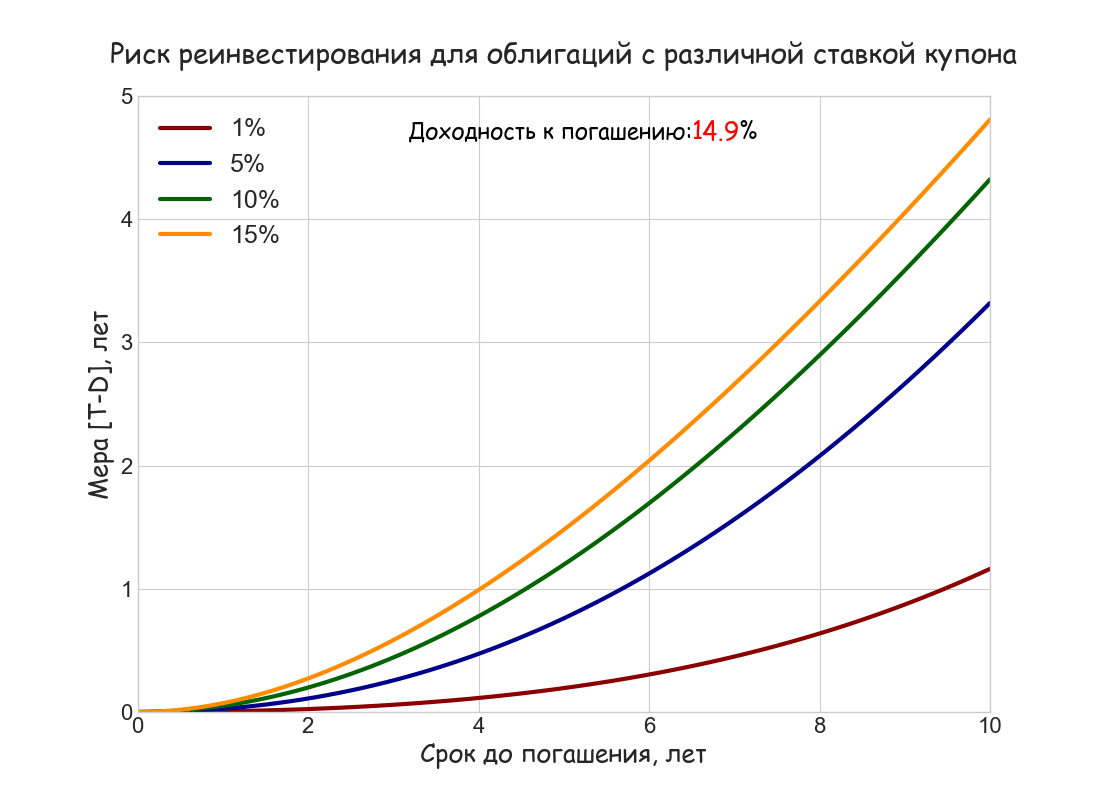
Численный пример 3. Инвестор приобрел за номинал 10-летнюю облигацию с купонной ставкой 10% и полугодовыми купонами. Каково будет примерное изменение накопленного дохода (в процентах), если сразу после покупки ставка дисконтирования упадет на 100 б. п. и останется неизменной до погашения облигации?

Первоначально инвестор рассчитывал получить накопленный доход в размере FV = 1000∙(1+5%)²⁰ = 2653.3 ден. ед. После снижения ставки ему придется реинвестировать получаемые купоны уже под меньшую номинальную доходность, 9% годовых; изменение ставки реинвестирования Δr.r. = —100 б. п. Дюрацию Маколея можно найти с помощью функции Excel, D = 6.76 лет. Используя приближенную формулу, получим

ΔFV/FV ≈ [10 — 6.76]/[1+5%]∙( — 1%) ≈ —3%, т.е. величина накопленного дохода упадет примерно на 3%. Точный расчет дает величину нового накопленного дохода 2568.6 ден. ед., соответственно ΔFV/FV = (2568.6—2653.3)/2653.3 = —3.2%, а значит приближение неплохо работает даже при больших сроках погашения.

Сравнивая две меры, D и (T — D), можно заметить, что ценовой риск в каком-то смысле конкурирует с риском реинвестирования. Во-первых, повышение ставок отрицательно влияет на мгновенную стоимость портфеля, но положительно — на будущий накопленный доход, верно и обратное. Во-вторых, значимость этих рисков для инвестора противоположна в зависимости от предполагаемого срока удержания.

Допустим, инвестор приобрел T-летнюю бумагу, а затем анализирует, что будет, если продать ее раньше — через полгода, год, пять лет, вплоть до срока погашения. Он заметит, что чем меньше предполагаемый срок удержания, тем выше риск изменения цены (больше оставшаяся дюрация) Ценовой риск исчезает на горизонте, совпадающим с датой погашения облигации. И на этом же горизонте максимальным становится риск реинвестирования, который почти не имеет значения при краткосрочных вложениях.

Как раз в точке дюрации совместное влияние этих рисков на будущую стоимость портфеля находится в равновесии. Принцип такого равновесия можно сформулировать следующим образом:

Дюрация дает нам точку безразличия в результате однократного сдвига плоской кривой доходности. Она равна количеству времени, необходимому, чтобы первоначальные изменения как цены, так и ставки реинвестирования полностью компенсировали друг друга.

Это свойство дюрации используется для так называемой иммунизации портфеля облигаций. Рассмотрим пример 10-летней облигации с непрерывной выплатой купона по ставке 10%, продающуюся за номинал в 1 ден. ед. Ее доходность к погашению (при непрерывном начислении процентов) также составляет 10%. Планируемый накопленный доход на горизонте 10 лет, FV = 2.72 ден. ед. Предположим, что сразу после покупки облигации рыночные ставки изменились на величину Δr и после этого остались такими же вплоть до погашения. В момент скачка доходности немедленно изменятся как цена облигации, так и прогнозируемый денежный поток от реинвестирования купонов.

Возможны два варианта:

1. При падении ставки цена облигации увеличится, P > 1, но реинвестирование купонов под более низкий процент уменьшит накопленную стоимость на момент погашения. Инвестор получит меньше, чем планировал изначально: FV < 2.72 ден. ед.
2. С повышением ставки все обстоит ровно наоборот — цена упадет, P <1, а реинвестирование купонов под более высокий процент принесет дополнительный доход, так что через 10 лет FV > 2.72 ден. ед.

Можно показать, что существует такой срок удержания T*, при котором, независимо от знака и величины изменения ставки, накопленный доход FV(T*) будет не меньше дохода, который первоначально рассчитан для того же срока. Оказывается, этот срок равен дюрации облигации D = 6.32 лет. Данный эффект хорошо заметен на рисунке:

Ниже также построен анимированный график относительного прироста капитала ΔFV/FV в зависимости от величины изменения доходности Δr = [—5%; 5%] Движущаяся кривая отражает изменение срока удержания позиции t от 0 до 10 лет. Видно, что только на сроке, равном дюрации, всегда выполнено неравенство ΔFV/F

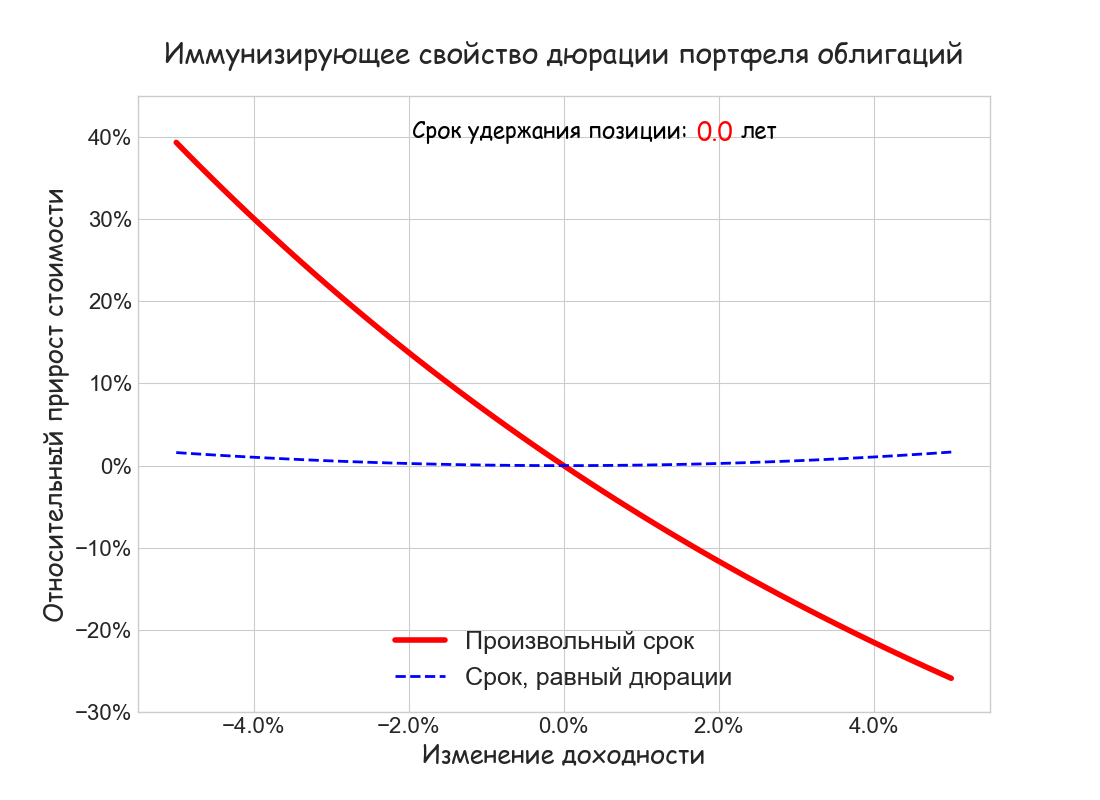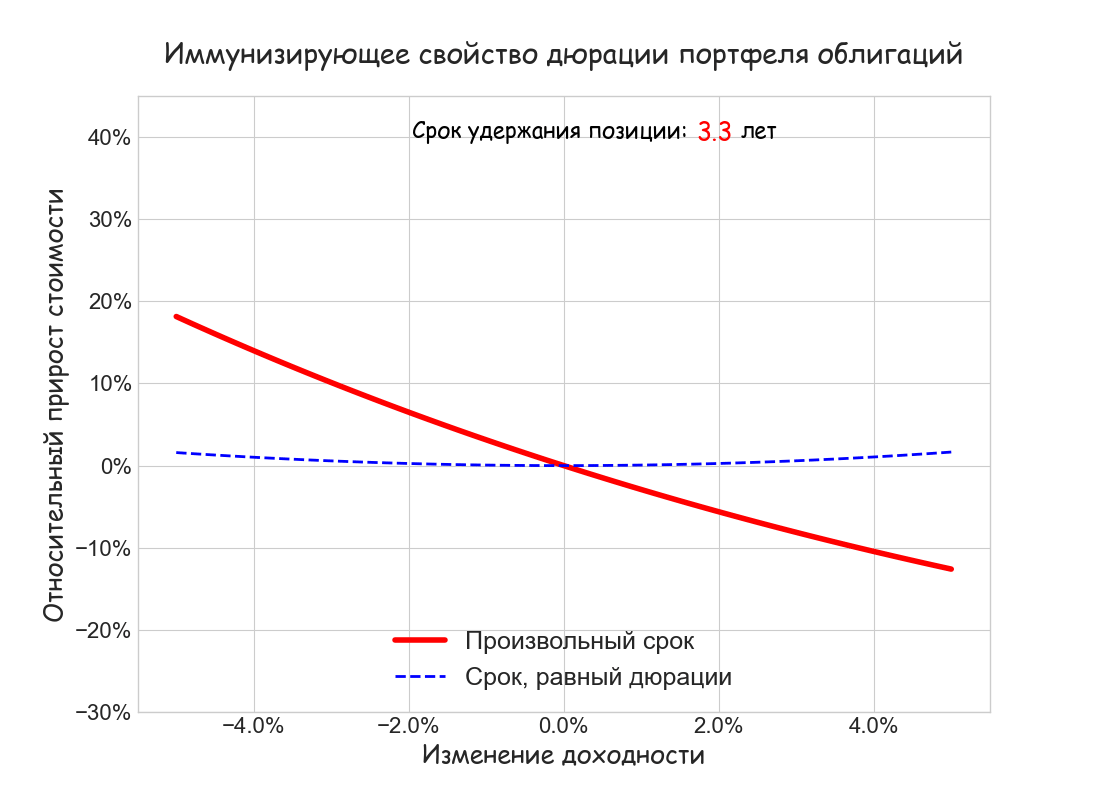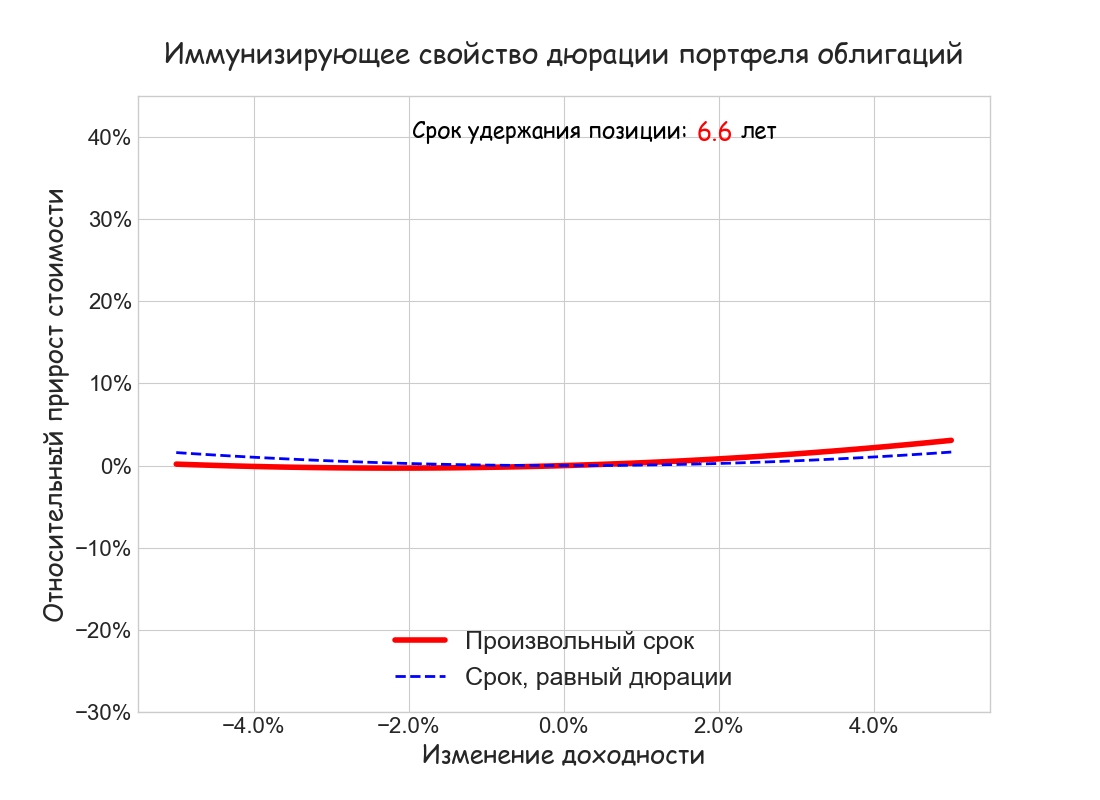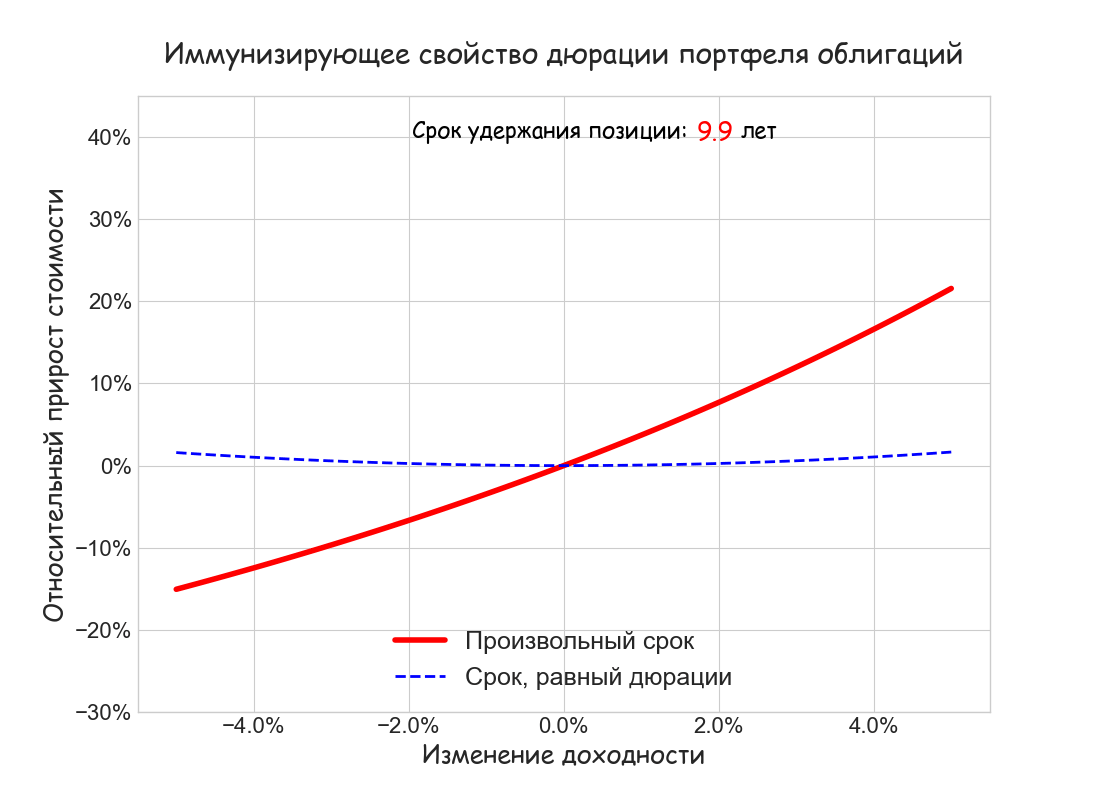
Таким образом, иммунизирующее свойство дюрации заключается в следующем:

При однократном изменении доходности портфеля его накопленная стоимость будет не меньше планируемой, если горизонт инвестора равен дюрации портфеля.