Модель скрытых состояний Маркова. Часть 2
В предыдущей статье мы говорили об эффективных алгоритмах, необходимых для вычисления вероятностей и стат. распределений модели Маркова, которыми являются форвардный алгоритм и алгоритм Витерби. Форвардный алгоритм вычисляет вероятность соответствия данных наблюдения полученным моделью всем возможным последовательностям состояний. Алгоритм Витерби вычисляет вероятность соответствия данных полученной моделью одной, наиболее вероятной, последовательности.
В этом посте будет много формул, но без этого не обойтись, чтобы создать хорошую стратегию, надо разбираться в математической модели, лежащей в ее основе. Следующие части будут более приближенными к практике.
Форвардный алгоритм.
Форвардный алгоритм позволяет эффективно рассчитать функцию вероятности p(O|λ). Форвардной переменной называется вероятность генерации моделью наблюдений до времени t, и состояние j в момент времени t определяется как:
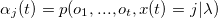
Это выражение вычисляется рекурсивно через форвардную переменную в момент времени t-1, находясь в состоянии k, и затем вычисляется состояние j в момент времени t:
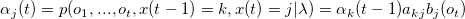
где akj — вероятность перехода из состояния k в состояние j, и bj(ot)- вероятность генерации вектора параметров ot из состояния t.
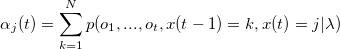
1. Инициализация алгоритма.
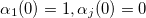для 1< j ≤ N и
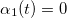для 1< t ≤ T
2. Рекурсия.
Для t=1,2,...,T
… для j=2,3,....,N−1
................![\alpha_j(t)=b_j(o_t)[\sum_{k=1}^{N-1}\alpha_k(t-1)a_{kj}]](http://mathurl.com/p45c8f9.png "Модель скрытых состояний Маркова. Часть 2")
3. Решение.
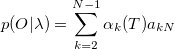
Алгоритм Витерби.
Форвардный алгоритм находит p(O|λ) суммированием по всем возможным последовательностям состояний, но иногда предпочтительней аппроксимировать p(O|λ) вероятностью p^(O|λ) которая вычисляется для одной, наиболее вероятной последовательности. Для этого применяется алгоритм Витерби:
![\hat{p}(O|\lambda)=\max_X[p(O,X|\lambda)]](http://mathurl.com/oz3r7bk.png "Модель скрытых состояний Маркова. Часть 2")
, где X — наиболее вероятная последовательность состояний.
Вероятность лучшего пути длиной t по модели Маркова, заканчивающегося состоянием j определяется как:
![\phi_j(t)=\max_{X^{t-1}}[p(o_1,...,o_t, x(t)=j|\lambda)]](http://mathurl.com/o8pmkpz.png "Модель скрытых состояний Маркова. Часть 2")
, где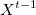 
— лучший путь/последовательность состояний.
Форвардная переменная ϕ также может быть вычислена рекурсивно:
![\phi_j(t)=\max_i[\phi_i(t-1)a_{ij}b_j(o_t)]](http://mathurl.com/m7kuqqb.png "Модель скрытых состояний Маркова. Часть 2")
1. Инициализация алгоритма.
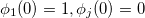для 1< j < N и 
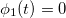для 1≤ t ≤ T
2. Рекурсия.
Для t=1,2,...,T
… для j=2,3,...,N−1
....................![\phi_j(t)=\max_{1\leq k<N}[\phi_k(t-1)a_{kj}]b_j(o_t)](http://mathurl.com/oetohbn.png "Модель скрытых состояний Маркова. Часть 2")
… сохранить предыдущее значение pred(j,t)=k
3. Решение.
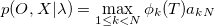
сохранить предыдущее значение pred(N,T)=k.
Наилучший путь находится путем следования по сохранненым значениям в обратном порядке по pred(j,t).
Ошибки малой разрядности
Прямое вычисление p(O|λ) может привести к ошибкам малой разрядности. Значение вероятности может быть таким маленьким, что компьютер не сможет рассчитать его верно. Вместо этого необходимо использовать вычисление натурального логарифма log(p(O|λ).
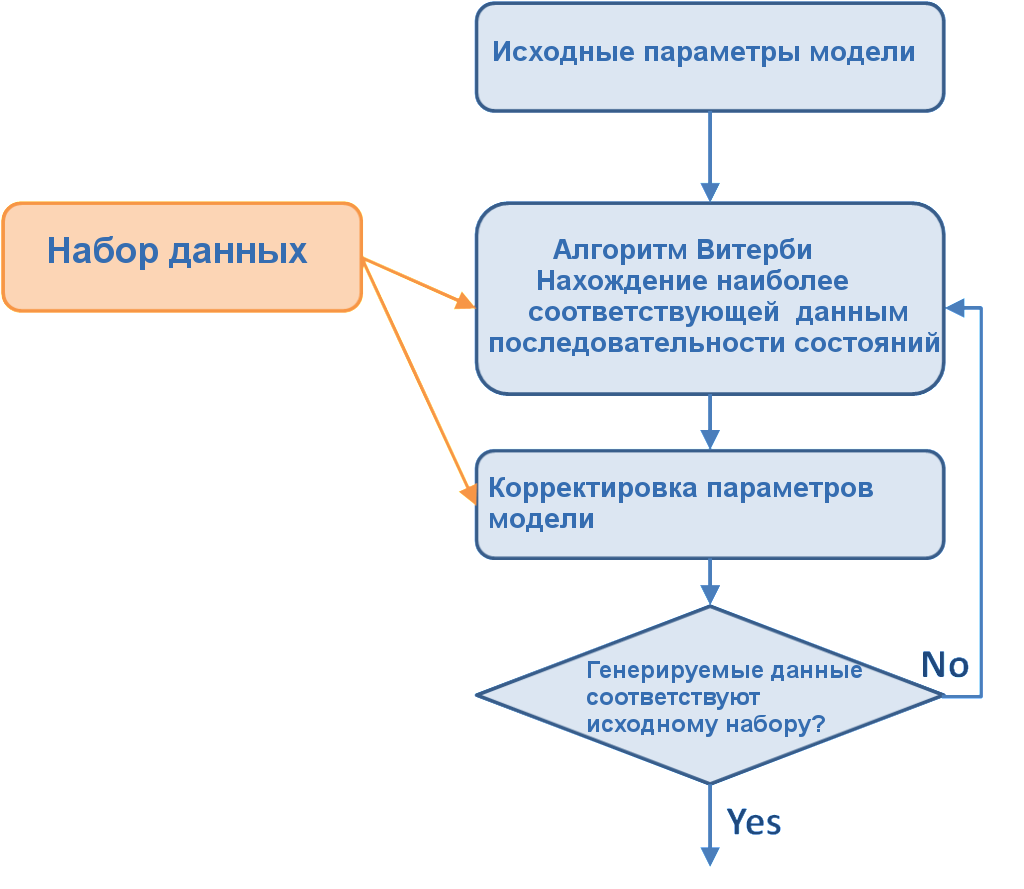
В следующей части цикла рассмотрим тренировку модели Маркова на сгенерированных входных данных с помощью реализации разобранных выше алгоритмов на языке R.
Другие стратегии, применяемые в алгоритмической торговле и биржевых роботах смотрите в моем блоге и на сайте.
Во вторых, не надо ля-ля про дифуры.
В третьих, по слухам, на этом если кто и смог заработать, так это Ренессанс Текноложди.
И как определить скольк овобще состояний имеет модель(например цнновой ряд) На глаз опрделеять или есть какие-то рекомендации?
То что тогда делать? ну тоесть они в случайном порядке идут и с разной периодичностью? Почти как рендом волк
Предположим у нас был сигнал (10 мин цена идет вверх- значит это тренд.А потом этот же сигнал перестанет работать.10 мин цена шла вверх, А дальше она не пойдет вверх, а наоборот боковик или вниз. Получается, что нужна какая-то оптимизация на истории.Мы берем нбеольшой промежуток веремени 10мин и по нему опрделеяем куда цена идет дальше.Если 10мин шло вверх-то тренд. Но как мне кажется у нас такая ситуацию не часто будет встречаться, а чаще будет угадайка, что произойдет если цена 10мин шла вверх? Исходя из исторических данных вряд ли это даст нам сигнал, Который с высокой вероятностью(70%, что цена после 10мин вверх и дальше еще 10-20мин будет идти вверх)