09 августа 2017, 17:05
Подводные камни программирования или как потерять производительность и не подать виду.
Обычно я просто читаю СМ и не лезу со своим «экспертным» мнением к людям. Но недавно я не выдержал и закусился на форуме, да еще и побил собственный рекорд, ушел в личный бан за 2 сообщения. Суть зарубы очень проста: утверждается что найти тренд можно не менее чем за 10млрд операций. За время чтения СМа я видел многое, но это похоже долго еще будет мой топ1 перлов по программированию.
Этот пост я написал для того самого человека, хотя он его и не увидит.
<Disclaimer>
Если ты настоящий программист за деньги, то ничего нового ты тут не найдешь.
Искать тренд мы пока не будем, а будем разбирать похожую задачу.
Для облегчения восприятия весь код написан на python.
</Disclaimer>
Дано: n случайных чисел
Найти: стандартное отклонение для последовательности из m чисел (m < n)
Искать тренд или стандартное отклонение от начала времен не совсем практично. Очевидно, что нужно выбирать некий временной интервал (возможно несколько) для которого будет считаться наша искомая величина, а дальше уже будет некая логика и экзекьюшн, и риск менеджмент, и все такое прочее.
Но вернемся к нашей задаче. Математика нам говорит что стандартное отклонение равно:
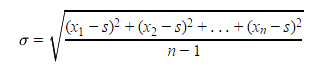
где s:

Ну что, решим эту задачку в лоб:
На закомментированные строчки пока внимание не обращаем.
Сначала немного магии, подключим нужные либы и объявим переменные.
Мы будем перебирать все элементы (n) добавляя новые к концу промежуточного массива (rng_elm), пока не наберем m элементов. После этого мы посчитаем среднее значение (rng_avr), потом квадрат разности (rng_n2). Ну и в конце мы сможем посчитать отклонение и вывести его на экран. Для всех последующих элементов мы будем делать тоже самое, только сначала будем удалять один элемент из начала промежуточного массива.
Запускаем скрипт, должно получится следующее:
Просто с самого начала нам нужно было немножко поиграть с формулой.

Прямо из формулы видно, что нам достаточно собирать сумму элементов и их квадратов. Перепишем код.
Заметьте что в этот раз я еще больше увеличил интервал, теперь он не 5000, а 50000.
Запускаем и видим что теперь на обработку одного шага тратится 0.00002 (2.3248035863250115e-05) секунды. А все потому что мы избавились от ненужных переборов массивов. В таком виде производительность нашей программы уже не зависит от интервала. Мы с вами магически превратили О(n^2) в О(n).
Зачем я все это написал? Да просто потому что могу.
Какой из этого можно сделать вывод? Ну наверное можно найти тренд и за 10млрд операций, но для этого нужно взять интервал в 1млрд значений. И тут у нормального человека должны появиться сомнения в смысле такой величины,
В комментариях предлагайте темы, возможно я смогу рассказать что-то интересное по ним в следующих сериях рубрики «Программирование для самых маленьких и тупых».
Этот пост я написал для того самого человека, хотя он его и не увидит.
<Disclaimer>
Если ты настоящий программист за деньги, то ничего нового ты тут не найдешь.
Искать тренд мы пока не будем, а будем разбирать похожую задачу.
Для облегчения восприятия весь код написан на python.
</Disclaimer>
Дано: n случайных чисел
Найти: стандартное отклонение для последовательности из m чисел (m < n)
Искать тренд или стандартное отклонение от начала времен не совсем практично. Очевидно, что нужно выбирать некий временной интервал (возможно несколько) для которого будет считаться наша искомая величина, а дальше уже будет некая логика и экзекьюшн, и риск менеджмент, и все такое прочее.
Но вернемся к нашей задаче. Математика нам говорит что стандартное отклонение равно:
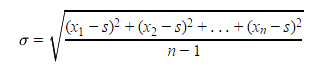
где s:
Ну что, решим эту задачку в лоб:
from math import sqrt
import random
import time
#n = [random.randint(0, 10) for i in range(10000)]
n = [3, 5, 0, 2, 1, 4, 5, 4, 1, 1, 1, 2, 5, 2, 1, 1, 5, 2, 4, 1]
print(n)
rng = 5
stddev = .0
rng_avr = .0
rng_n2 = .0
rng_elm = []
time_exe = []
tsum = .0
for i in range(len(n)):
#start_time = time.time()
rng_elm.append(n[i])
if i < rng - 1:
continue
elif i == rng - 1:
for j in rng_elm:
rng_avr += j/rng
for j in rng_elm:
rng_n2 += pow((j - rng_avr),2)
stddev = sqrt(rng_n2/(rng-1))
print ('\tstddev: %.5f' % stddev)
#time_exe.append((time.time() - start_time))
else:
rng_n2 = .0
rng_avr = .0
rng_elm.pop(0)
for j in rng_elm:
rng_avr += j/rng
for j in rng_elm:
rng_n2 += pow((j - rng_avr),2)
stddev = sqrt(rng_n2/(rng-1))
print ('\tstddev: %.5f' % stddev)
#time_exe.append((time.time() - start_time))
#for i in time_exe:
# tsum += i/len(time_exe)
#print(tsum)На закомментированные строчки пока внимание не обращаем.
Сначала немного магии, подключим нужные либы и объявим переменные.
Мы будем перебирать все элементы (n) добавляя новые к концу промежуточного массива (rng_elm), пока не наберем m элементов. После этого мы посчитаем среднее значение (rng_avr), потом квадрат разности (rng_n2). Ну и в конце мы сможем посчитать отклонение и вывести его на экран. Для всех последующих элементов мы будем делать тоже самое, только сначала будем удалять один элемент из начала промежуточного массива.
Запускаем скрипт, должно получится следующее:
[3, 5, 0, 2, 1, 4, 5, 4, 1, 1, 1, 2, 5, 2, 1, 1, 5, 2, 4, 1] stddev: 1.92354 stddev: 2.07364 stddev: 2.07364 stddev: 1.64317 stddev: 1.87083 stddev: 1.87083 stddev: 1.94936 stddev: 1.30384 stddev: 1.73205 stddev: 1.64317 stddev: 1.64317 stddev: 1.64317 stddev: 2.04939 stddev: 1.64317 stddev: 1.81659 stddev: 1.81659Ну что ж, все работает. Можно переходить к следующему шагу. Удаляем все #, кроме верхней строчки. Там нужно переписать вот так:
n = [random.randint(0, 10) for i in range(10000)] #n = [3, 5, 0, 2, 1, 4, 5, 4, 1, 1, 1, 2, 5, 2, 1, 1, 5, 2, 4, 1] #print(n) rng = 5000Запускаем снова и видим что время на обработку одного шага у нас примерно равно 0.0019 секунды. И тут надо бы задать вопрос: А можно ли сделать это быстрее? Конечно можно!
Просто с самого начала нам нужно было немножко поиграть с формулой.

Прямо из формулы видно, что нам достаточно собирать сумму элементов и их квадратов. Перепишем код.
from math import sqrt
import random
import time
n = [random.randint(0, 10) for i in range(100000)]
#n = [3, 5, 0, 2, 1, 4, 5, 4, 1, 1, 1, 2, 5, 2, 1, 1, 5, 2, 4, 1]
#print(n)
stddev = .0
rng = 50000
rng_sum = 0
rng_n2 = 0
rng_elm = []
time_exe = []
tsum = .0
for i in range(len(n)):
start_time = time.time()
rng_sum += n[i]
rng_n2 += n[i]*n[i]
rng_elm.append(n[i])
if i < rng - 1:
continue
elif i == rng -1:
stddev = sqrt((rng_n2 - (rng_sum*rng_sum/rng))/(rng-1))
print ('\tstddev: %.5f' % stddev)
time_exe.append((time.time() - start_time))
else:
dif = rng_elm.pop(0)
rng_sum -= dif
rng_n2 -= dif*dif
stddev = sqrt((rng_n2 - (rng_sum*rng_sum/rng))/(rng-1))
print ('\tstddev: %.5f' % stddev)
time_exe.append((time.time() - start_time))
for i in time_exe:
tsum += i/len(time_exe)
print(tsum)Можно убедиться что считается все одинаково закомментировав все как в первом куске кода и выставив rng = 5.Заметьте что в этот раз я еще больше увеличил интервал, теперь он не 5000, а 50000.
Запускаем и видим что теперь на обработку одного шага тратится 0.00002 (2.3248035863250115e-05) секунды. А все потому что мы избавились от ненужных переборов массивов. В таком виде производительность нашей программы уже не зависит от интервала. Мы с вами магически превратили О(n^2) в О(n).
Зачем я все это написал? Да просто потому что могу.
Какой из этого можно сделать вывод? Ну наверное можно найти тренд и за 10млрд операций, но для этого нужно взять интервал в 1млрд значений. И тут у нормального человека должны появиться сомнения в смысле такой величины,
В комментариях предлагайте темы, возможно я смогу рассказать что-то интересное по ним в следующих сериях рубрики «Программирование для самых маленьких и тупых».










Надо строго за O(N)
и я не понимаю, откуда берется 1440 в квадрате. Что-то некорректно в ваших расчетах.
1440 — минут в сутках (размеры окна, в котором считаем)
10 — число лет данных
252 — число дней в каждом году данных
1440 — число минут в каждом дне данных
В принципе, для расчета выборочного к-та асимметрии достаточно получить оценку второго и третьего центрального моментов. Они строятся комбинацией из сумм данных в окне, их квадратов и кубов. Ну, корень еще появится.
Чтобы это делать в скользящем окне, нужно посчитать эти числа для первого окна, а потом на каждом такте вычесть выбывающий элемент и прибавить входящий.
Объем вычислений будет const* N, где N=10*252*1440
Как сделать быстро — можете не писать, я знаю. Я же и поставил доп. условие — без потери точности.
А вот здесь описанная вами схема
не работает — происходит накопление ошибок порядка sqrt(машинная точность), которая при возведении в куб и последующего деления на числа с такими ошибками — дают вообще непредказуемые по масштабам ошибки в результате.
Вы не поверите — уже даже в окне 3-4 начинаются косяки из-за машинного округления double'ов, т.е. реализация схемы с прибавлением-вычитанием «в лоб» дает сильно плохой результат при расчете skewnessa / kurtosisa
Если все так плохо, надо подумать о других методах, более устойчивых. Не в смысле наращивания разрядности, а в содержательном смысле. Есть же меры асимметрии, допустим, которые не завязаны на центральные моменты.
К сожалению, даже с алгоритмом Кэхэна не удалось получить удобоваримый результат на малых окнах. В итоге пришлось решать задачу на машинном уровне.
А то что Вы говорили, что типа он тут дает какое то большое преимущество в читабельности, это навяд ли, цЫклы они и в Африке цЫклы:)
плюс этот код может взять любой и быстро у себя запустить и проверить.
И по первой формуле среднеквадратичного отклонения она работает только при n<40 при n>40 разность квадратов.
Не проще использовать метод последовательного анализа для проверки гипотез? в среднем метод требует в 2 раза меньше испытаний, чем классический метод проверки гипотезы.
MadQuant иногда пишет. Я так понял корзины инструментов прогнанные на истории в 15 лет