22 февраля 2018, 15:01
Коинтегрированные пары: аналитика за 2017 год на Мосбирже
В данном блог-посте будут представлены результаты исследования за 2017 год коинтегрированных пар акций, которые торгуются на Московской бирже. Методика тестирования основана на тесте Энгла-Грэнджера, но для начала проясним некоторые моменты про стационарность, возникшие в предыдущем блог-посте.
Напомню, что если говорить про стационарность без каких-либо формул и сложных понятий, то смысл в том, что стационарный ряд не меняет со временем свои характеристики, такие как матожидание, дисперсия и ковариации.
Постоянное матожидание на графике приращений выявить относительно легко — он должен колебаться вокруг некоторого среднего значения — это и будет постоянным матожиданием, а вот что касается дисперсии… во-первых, это мера разброса, и её нельзя изобразить на графике ряда, во-вторых, она может быть постоянной даже с неровными зубьями на графике и, в-третьих, насколько я поняла, суть стационарности не в ровной высоте зубьев, а в возврате к среднему. То есть когда мы видим график, который колеблется вокруг некоего постоянного значения, удаляется от него, а затем возвращается обратно, то такой ряд вполне может быть стационарным. Именно это свойство возврата к среднему нам и ценно в AR(1)-моделях.
Замечу также, что помимо AR(1)-моделей ранее я исследовала ещё и GBM-модели, и там выяснилось, что логарифм цены также имеет стационарные приращения.
Благодаря ch5oh удалось обнаружить ошибку в результатах интерпретации ADF-теста. После перерасчёта получилось 277 акций со стационарными приращениями. Приведу для примера график изменения цены одной из таких акций, а также график её приращений.
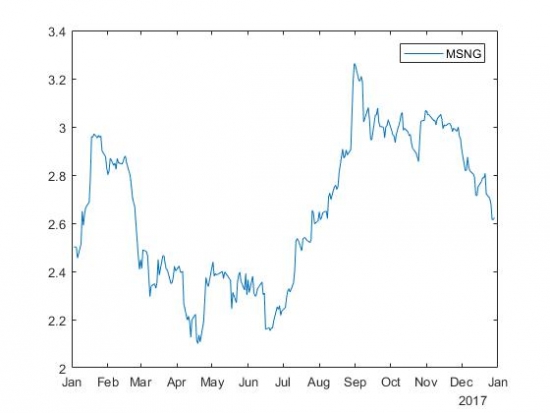
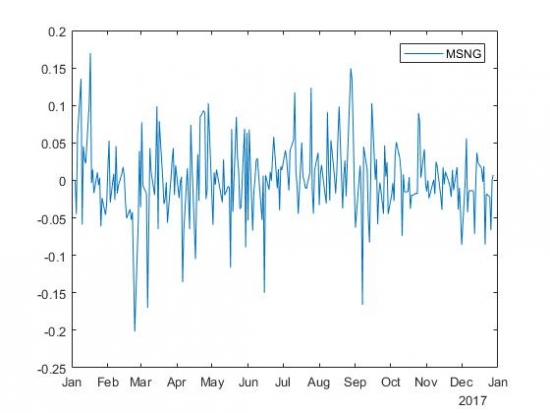
На графике приращений видно, что зубья разной длины. Однако, ряд то и дело возвращается к среднему, поэтому можно согласиться с тем, что он стационарный.
Дальше встаёт вопрос: а зачем нам нужны акции со стационарными приращениями? Для того, чтобы составить из них коинтегрированные пары.
Всего было протестировано 32385 пар. В случае регрессии без свободного члена получилось 8287 коинтегрированных пар, но не все модели были хорошими. Я отфильтровала модели с коэффициентом детерминации не менее 50%, чтобы получить набор из приемлемых моделей. Получилось 3483 пары. Изобразим одну из них: (MSNG, MRSB).
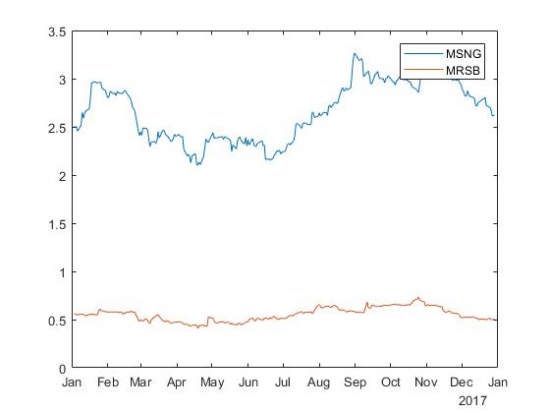
Разность цен акций MSNG и MRSB с коэффициентом бета, равным 4,7796:
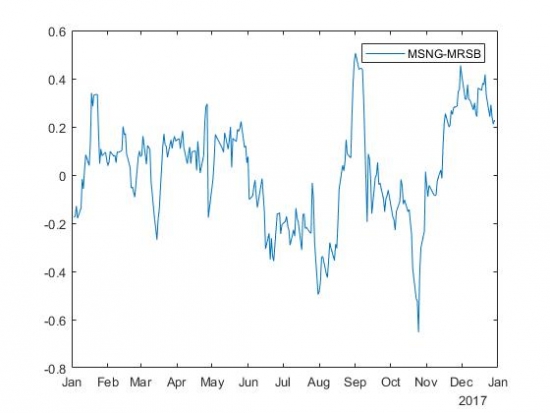
Затем я отфильтровала модели с коэффициентом детерминации не менее 80%, чтобы получить набор из достаточно хороших моделей. Получилось 102 пары. Изобразим одну из них. Цены акций MSNG и OGKB:
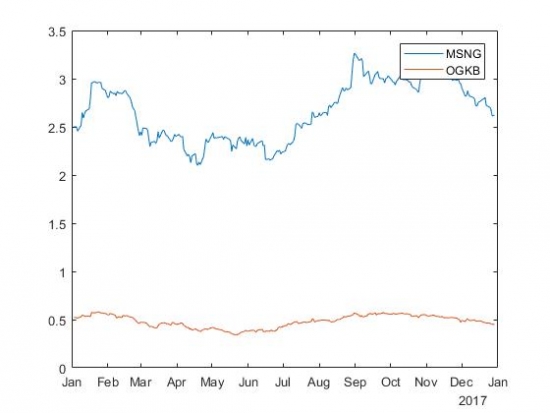
Разность цен акций MSNG и OGKB с коэффициентом бета, равным 5,4827:
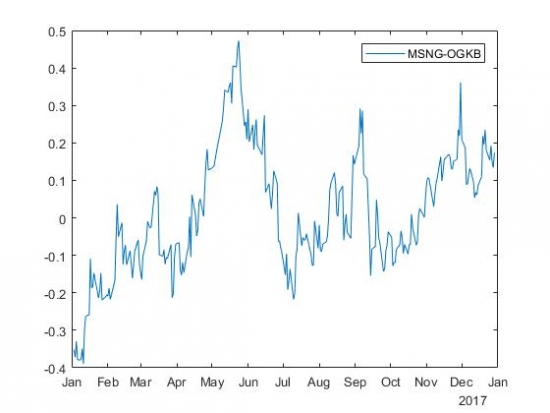
Ну и дальше я отфильтровала модели с коэффициентом детерминации не менее 90%. Получилось 4 пары. Изобразим одну из них. Цены акций SBERP и MSTT:
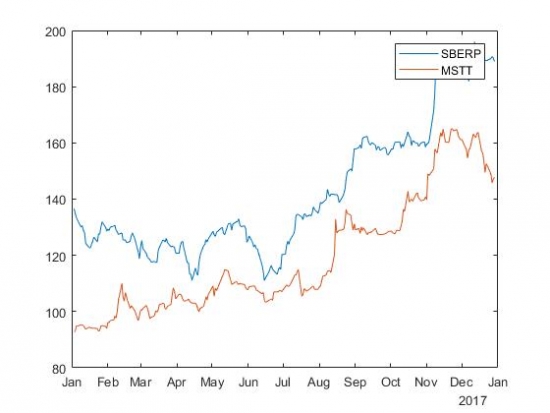
Разность цен акций SBERP и MSTT с коэффициентом бета, равным 1,1928:
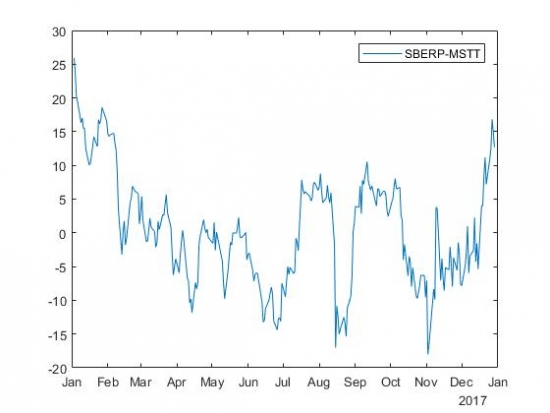
В следующем блог-посте я покажу результаты по доходности на бэктестах.
Стационарность
У нас вышел спор насчёт того, стационарные ли приращения у акций или нет. ch5oh говорил, что очевидно, что на рынке у всех акций приращения стационарны. SergeyJu — что очевидно, что на рынке нет ни одной акции со стационарными приращениями, и что RW-модель, используемая для описания цены акции, неадекватна. Первый вопрос, который здесь возникает: а как по графику понять, стационарный ряд или нет?Напомню, что если говорить про стационарность без каких-либо формул и сложных понятий, то смысл в том, что стационарный ряд не меняет со временем свои характеристики, такие как матожидание, дисперсия и ковариации.
Постоянное матожидание на графике приращений выявить относительно легко — он должен колебаться вокруг некоторого среднего значения — это и будет постоянным матожиданием, а вот что касается дисперсии… во-первых, это мера разброса, и её нельзя изобразить на графике ряда, во-вторых, она может быть постоянной даже с неровными зубьями на графике и, в-третьих, насколько я поняла, суть стационарности не в ровной высоте зубьев, а в возврате к среднему. То есть когда мы видим график, который колеблется вокруг некоего постоянного значения, удаляется от него, а затем возвращается обратно, то такой ряд вполне может быть стационарным. Именно это свойство возврата к среднему нам и ценно в AR(1)-моделях.
Замечу также, что помимо AR(1)-моделей ранее я исследовала ещё и GBM-модели, и там выяснилось, что логарифм цены также имеет стационарные приращения.
Благодаря ch5oh удалось обнаружить ошибку в результатах интерпретации ADF-теста. После перерасчёта получилось 277 акций со стационарными приращениями. Приведу для примера график изменения цены одной из таких акций, а также график её приращений.


На графике приращений видно, что зубья разной длины. Однако, ряд то и дело возвращается к среднему, поэтому можно согласиться с тем, что он стационарный.
Дальше встаёт вопрос: а зачем нам нужны акции со стационарными приращениями? Для того, чтобы составить из них коинтегрированные пары.
Коинтегрированные пары
Про метод тестирования на наличие коинтеграции я подробно писала в статье на хабре. Я бы с радостью продублировала всю информацию здесь, но тут сложно вставлять красивые формулы, поэтому я просто приведу результаты.Всего было протестировано 32385 пар. В случае регрессии без свободного члена получилось 8287 коинтегрированных пар, но не все модели были хорошими. Я отфильтровала модели с коэффициентом детерминации не менее 50%, чтобы получить набор из приемлемых моделей. Получилось 3483 пары. Изобразим одну из них: (MSNG, MRSB).

Разность цен акций MSNG и MRSB с коэффициентом бета, равным 4,7796:

Затем я отфильтровала модели с коэффициентом детерминации не менее 80%, чтобы получить набор из достаточно хороших моделей. Получилось 102 пары. Изобразим одну из них. Цены акций MSNG и OGKB:

Разность цен акций MSNG и OGKB с коэффициентом бета, равным 5,4827:

Ну и дальше я отфильтровала модели с коэффициентом детерминации не менее 90%. Получилось 4 пары. Изобразим одну из них. Цены акций SBERP и MSTT:

Разность цен акций SBERP и MSTT с коэффициентом бета, равным 1,1928:

В следующем блог-посте я покажу результаты по доходности на бэктестах.










На Московской бирже в качестве цены закрытия для акций используется цена аукциона закрытия. Я понимаю, что во время этого аукциона никаких действий с акциями я делать не могу, но нам и не нужно ничего делать с акциями во время ПТА.
Нам нужна цена закрытия, чтобы рассчитать коэффициент коинтеграции. Цена закрытия — это просто некий расчётный показатель, который нам нужен, чтобы оценить актив. А торговать мы будем внутри дня, причём не по цене закрытия.
А теперь, выясняется, что и с данными у Вас и с вычислительными мощностями проблемы. Остается вопрос, а как Вам удалось узнать, что ценой бОльших затрат будет получен тот же ответ. Я вижу, что ценой некоторого усложнения расчетов получается гораздо более мощная и адекватная конструкция.
Возьмём ГСЧ (хороший!) и сделаем им, ну допустим, 3000 заведомо независимых логнормальных синтетических рядов дневок за 10 лет. Ну матожидание положим ноль, сигма 20 годовых. Будем считать, что эмулируем рынок более-менее tradeble акций США.
Далее выбираем некое разумное окно, скользким им, считаем гренджера, дики-фуллера и прочее. Все как полагается.
И получаем какой то процент percent_synth локально коинтегрированных участков некоторых пар.
Внимание, вопрос: будет ли percent_synth значимо отличаться от percent_real?