13 марта 2021, 16:53
Физико-математические основы Грааля. Часть 9. Нестационарность рынка.
Вспоминаю диалог с Колдуном:
— Запомни, рынок стационарен в узком смысле, однако, страждущие не могут это узреть. Ищи стационарность и обрящешь.
— Слушаюсь, Мастер...
— Ступай, Тень, и не тревожь меня более.
Как же так? Какая еще стационарность? Ведь всем известно, что никакой стационарности нетути, что рынок нестационарен по определению и этот факт является первопричиной отсутствия стабильно зарабатывающей торговой системы практически у всех трейдеров...
Если исходить из парадигмы немарковского случайного процесса, описываемого уравнением:
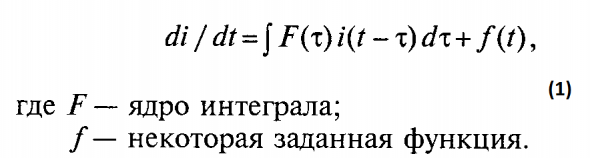
то, очевидно, что на рынке f(t) — это плотность вероятности тиковых приращений, которая является предопределенной для каждой валютной пары и принадлежит к классу гамма-распределений.
Примем за основную гипотезу, что генеральная совокупность приращений образует именно заданную плотность вероятности некоего ГПСЧ (в теме https://smart-lab.ru/blog/616897.php было показано, что данный ГПСЧ представляет из себя произведение СЧ гауссовского распределения и распределения Эрланга, т.е. расстояния, которые проходит броуновская частица за экспоненциальные промежутки времени).
В этом случае, мы вправе использовать известную формулу Эйнштейна-Смолуховского:

Для семейства гамма-распределений, коэффициент диффузии D определяется выражением:
D = S*(b^2)
где
S — некий параметр формы данного распределения, а b - это среднее значение модулей приращений

при N --> к бесконечности.
Фактически, мы постулируем, что параметр b = const и является уникальным для каждой валютной пары.
Т.о. рынок действительно является стационарным в том смысле, что распределение тиковых приращений для каждой валютной пары является неизменным и задается раз и навсегда. А то, что мы видим на примере выборок из генеральной совокупности приращений — это ерунда и использовать в расчетах выборочные дисперсию и матожидание распределения приращений нельзя ни в коем случае.
Поэтому, в формуле

нестационарным остается только интенсивность tau (количество пришедших тиков за определенный промежуток времени) тикового потока котировок.
Что же с этим делать?
А, пожалуй, — ничего. Надо принять это «как есть» ибо так посоветовал Волшебник.
Посмотрим график для пары AUDCHF за случайный промежуток времени
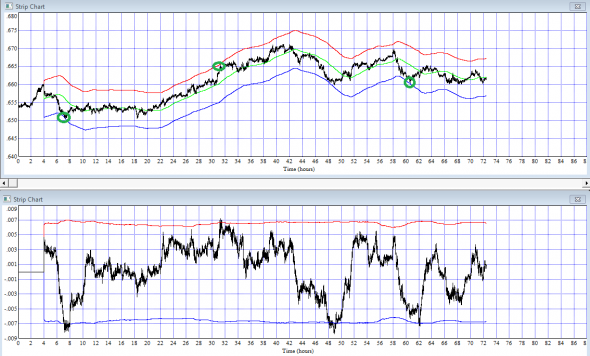
Точки входа отмечены зелеными кружками.
Выход — при возврате к средней.
На нижнем графике видно, что дисперсионный канал незначительно меняется при изменении интенсивности тикового потока котировок, но, в целом это не оказывает существенного влияния на стратегию.
До встречи.
Toddler.
PS
Только — тсссс… Никому — ни слова, ни полслова об услышанном. Колдун и Девять Стражей Грааля осерчать могут. Помилосердствуйте....
— Запомни, рынок стационарен в узком смысле, однако, страждущие не могут это узреть. Ищи стационарность и обрящешь.
— Слушаюсь, Мастер...
— Ступай, Тень, и не тревожь меня более.
Как же так? Какая еще стационарность? Ведь всем известно, что никакой стационарности нетути, что рынок нестационарен по определению и этот факт является первопричиной отсутствия стабильно зарабатывающей торговой системы практически у всех трейдеров...
Если исходить из парадигмы немарковского случайного процесса, описываемого уравнением:
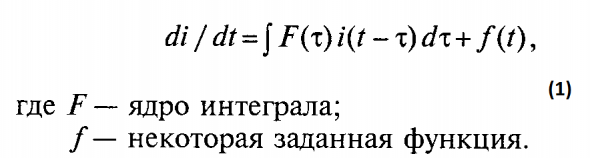
то, очевидно, что на рынке f(t) — это плотность вероятности тиковых приращений, которая является предопределенной для каждой валютной пары и принадлежит к классу гамма-распределений.
Примем за основную гипотезу, что генеральная совокупность приращений образует именно заданную плотность вероятности некоего ГПСЧ (в теме https://smart-lab.ru/blog/616897.php было показано, что данный ГПСЧ представляет из себя произведение СЧ гауссовского распределения и распределения Эрланга, т.е. расстояния, которые проходит броуновская частица за экспоненциальные промежутки времени).
В этом случае, мы вправе использовать известную формулу Эйнштейна-Смолуховского:
Коэффициент диффузии броуновской частицы связывает средний квадрат её смещения x (в проекции на произвольную фиксированную ось) и время наблюдения τ:

Для семейства гамма-распределений, коэффициент диффузии D определяется выражением:
D = S*(b^2)
где
S — некий параметр формы данного распределения, а b - это среднее значение модулей приращений

при N --> к бесконечности.
Фактически, мы постулируем, что параметр b = const и является уникальным для каждой валютной пары.
Т.о. рынок действительно является стационарным в том смысле, что распределение тиковых приращений для каждой валютной пары является неизменным и задается раз и навсегда. А то, что мы видим на примере выборок из генеральной совокупности приращений — это ерунда и использовать в расчетах выборочные дисперсию и матожидание распределения приращений нельзя ни в коем случае.
Поэтому, в формуле

нестационарным остается только интенсивность tau (количество пришедших тиков за определенный промежуток времени) тикового потока котировок.
Что же с этим делать?
А, пожалуй, — ничего. Надо принять это «как есть» ибо так посоветовал Волшебник.
Посмотрим график для пары AUDCHF за случайный промежуток времени

Точки входа отмечены зелеными кружками.
Выход — при возврате к средней.
На нижнем графике видно, что дисперсионный канал незначительно меняется при изменении интенсивности тикового потока котировок, но, в целом это не оказывает существенного влияния на стратегию.
До встречи.
Toddler.
PS
Только — тсссс… Никому — ни слова, ни полслова об услышанном. Колдун и Девять Стражей Грааля осерчать могут. Помилосердствуйте....










Сходимость суммы к b при N, стремящемся к бесконечности, говорит не о стационарности, а о некой форме ограниченности котировок (что естественно).
Стационарность у рядов приращений цен отсутствует (что несложно проверяется), а вот эргодичность в некоей форме присутствует. Что и позволяет проводить общие рассуждения.
С уважением
Но, это очень важный факт.
Фактически, нет необходимости исследовать выборочное распределение приращений.
Исследовать необходимо исключительно и только интенсивность потока котировок для применения в формуле Эйнштейна-Смолуховского.
Бесконечная сумма, левым концом уходящая в прошлое, требует либо знаний о бесконечном прошлом (что едва ли возможно), либо знаний о темпах роста или падения котировок на супердлинных периодах.
Здесь в теории можно попытаться подглянуть в будущее, но тогда мы должны принять, что стрела времени для ценовых котировок обратима (что вообще не очевидно). Ну и пока все, что мы знаем о темпах роста котировок — это то, что они почти никогда не растут быстрее, чем экспоненциально. Зато экспоненциальный рост бывает длинным.
Так что b в Вашем пределе легко может оказаться бесконечным.
И даже его конечность и уникальность для каждого актива ровным счетом ничего не говорит о стационарности и возможности отказа от выборочного распределения приращений.
С уважением
Идея родилась после общения с некоторыми трейдерами, которые абсолютно уверены, что процесс на рынке — искусственный, по заранее заданному ГПСЧ.
Если это так — то b=const и для каждой пары уникально. Это основной вывод данного поста.
А вот по какой формуле изменяется интенсивность тикового потока в определенном скользящем окне — загадка. Если это проанализировать, то выясняется, что интенсивность потока для разных часов внутри суток — разная, но тоже имеет очевидные закономерности «в среднем».
Т.о. ширина канала должна вычисляться не на основе данных предыдущего часа, что в принципе неверно, а на архивных статистических данных для данного конкретного часа.
Мне удалось построить разложение Уолда для приращений цен. Правда в виде бесконечного ряда и сходящегося в среднем (по Эйлеру или Борелю).
Отсюда вытекают и слабая форма эргодичности и (даже) некая слабая форма стационарности.
Что конечно не означает возможность применения в лоб формул для стационарного случая.
С уважением
Никаких других сходимостей в среднем для ценовых рядов не может быть в силу их конечности.
С Вами трудно дискутировать, т.к. буквально Вы безусловно правы. Но:
1. Я исследую ряды, бесконечно продолженные в прошлое (которое, разумеется, конечно, как рынок, Земля и вселенная...)
2. Ряды в несколько десятков и сотен тысяч слагаемых вполне могут исследоваться как бесконечные.
3. Связанные системы уравнений могут не иметь регулярных решений (решение каждой конкретной подсистемы существует, но они ни к чему не сходятся при увеличении количества уравнений в подсистеме), в то время как получающаяся по аналогии бесконечная система уравнений имеет решение.
Как-то так
С уважением
P.S. В стохастической математике также мало кто любит связываться с дискретными случаями, т.к. в таком раскладе формулы получаются громоздкие, ненаглядные и подходящие только для машинных расчетов.
Должен заметить, что между данными с маленьким временным лагом (менее 15 мин) и бОльшим временным лагом существуют некоторые статистически значимые неоднородности. По крайней мере на российских акциях внутри минуток преобладает контртренд, а выше 15 минуток его влияние исчезает. Статистика дневок отличается от статистик внутри дня.
Но ладно бы это. На макроуровне мы имеем уникальные события, которые не повторяются. Наш кризис 1998 года совсем не похож на кризис 2008 и не имеет аналогов в США. Великая депрессия тоже единичный феномен.
Так… Балуюсь… И на реальном счете немного зарабатываю.
Но, только немного… Это — правда.
А мне нужен Грааль.
Впрочем, все свои алгоритмы я проверяю на реальном счете. Через некоторое время опубликую результаты. Посмотрим…
Верно ли, что Вы излагаете модель броуновского движения фондового рынка, облагороженную введением нелинейного времени для получения удобного канала с характеристиками
по статистике суточных циклов?
Я очень сильно работаю в этом направлении.
Иногда мне кажется, что Сообщество Волшебников состоит вовсе не из людей…