Избранное трейдера Overlord
Код Уолл-cтрит (Видео)
- 15 июня 2015, 20:43
- |
Подписываемся на канал в YouTube: Investrim
- комментировать
- ★14
- Комментарии ( 0 )
Что случилось в 2015 году с fRTS ?
- 15 июня 2015, 00:39
- |
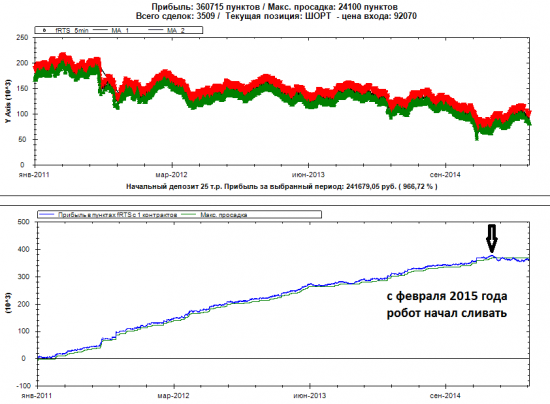
фишка была в том, что сам алгоритм примитивен до опупения… но работал..
вся логика — 5 строк кода
if (pr > max) { max = pr; ind = 1; } // — если обновляем максимум то в лонг
if (pr < min) { min = pr; ind = -1; } // — если обновляем минимум то в шорт
max -= k2; // максимум плавно опускаем каждую 5-минутку
min += k3; // минимум плавно поднимаем каждую 5-минутку
if ((ind == 1) && (pr < max- stop_long)) ind = 0; // если цена ниже максимума на размер стопа и мы лонге — выход кеш
( Читать дальше )
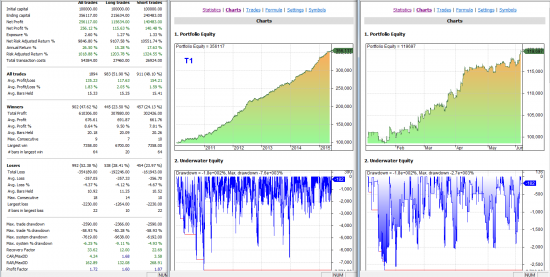
#SensorLive - Выкладываю общую эквити всех систем.
- 08 июня 2015, 14:44
- |
Показываю. Плюс эквити каждой системы за 5 лет и с начала 2015 года.
Предыдущие мои посты по своим системам тут и тут.
Условные обозначения: Т — трендовая тс. КТ — контр-трендовая тс.
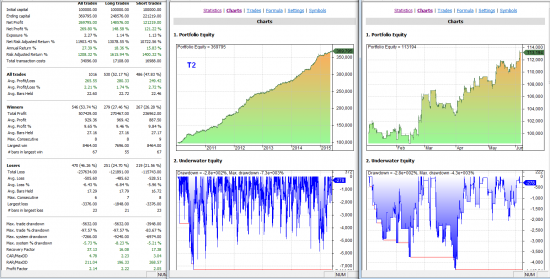
( Читать дальше )
Модель скрытых состояний Маркова. Часть 4
- 20 мая 2015, 14:06
- |
Окончание цикла статей. Начало и другие алгоритмы биржевой торговли смотрите в моем блоге и на сайте.
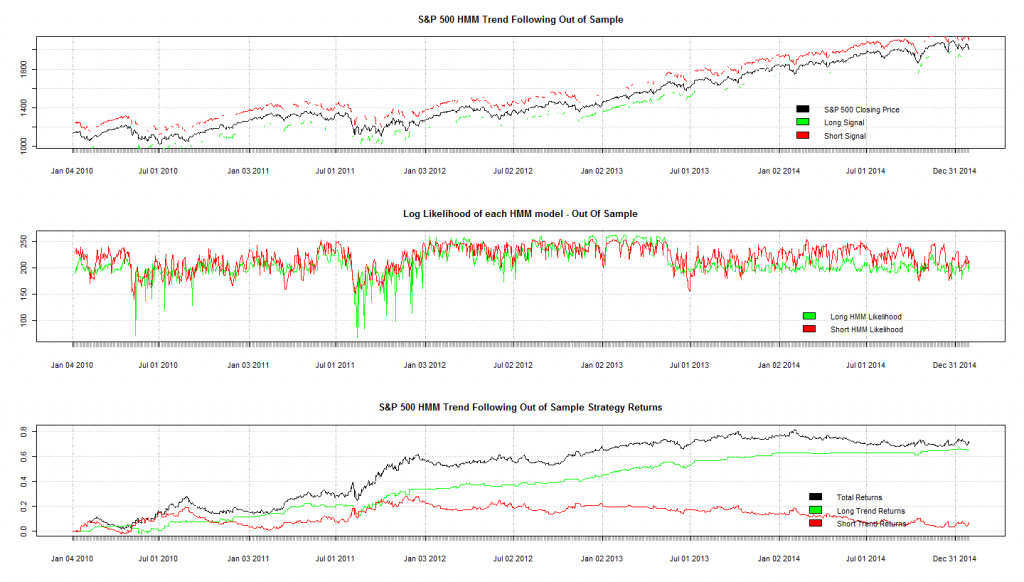
В прошлой части мы продемонстрировали обучение модели Маркова на данных, полученных с помощью симуляции. В данной статье рассмотрим производительность модели на реальных данных. Будем тестировать трендследящую стратегию на индексе S&P500.
В большинстве задач с использованием машинного обучения требуются обучающие данные с разметкой классов (состояний). В нашем случае такой разметки нет, поэтому сначала сгенерируем классы для обучающей выборки.
Мы хотим создать трендследящую стратегию, поэтому должны выбрать участки на выборке цен S&P500, которые соответствуют восходящему и нисходящему трендам ( также можно отметить участки, где тренды отсутствуют). Можно это сделать вручную, а можно применить программу, которая автоматически расставит метки в соответствии с вашими определениями тренда.
( Читать дальше )
Модель скрытых состояний Маркова. Часть 3
- 18 мая 2015, 14:01
- |
В этой части рассмотрим обучение модели скрытых состояний Маркова на языке R. В прошлых статьях мы изучили математическую основу модели, которая воплощена в библиотеке RHmm. Есть два способа распознавания режимов с помощью модели Маркова, первый — использование одной модели, каждое состояние которой отражает режим, в каком находится рынок. Второй способ подразумевает построение нескольких моделей, каждая из которых создана для одного режима, задача состоит в том, чтобы выбрать ту модель, которая генерирует данные, наиболее соответствующие текущему состоянию рынка. Рассмотрим оба эти способа.
Метод первый — одна модель с несколькими состояниями.
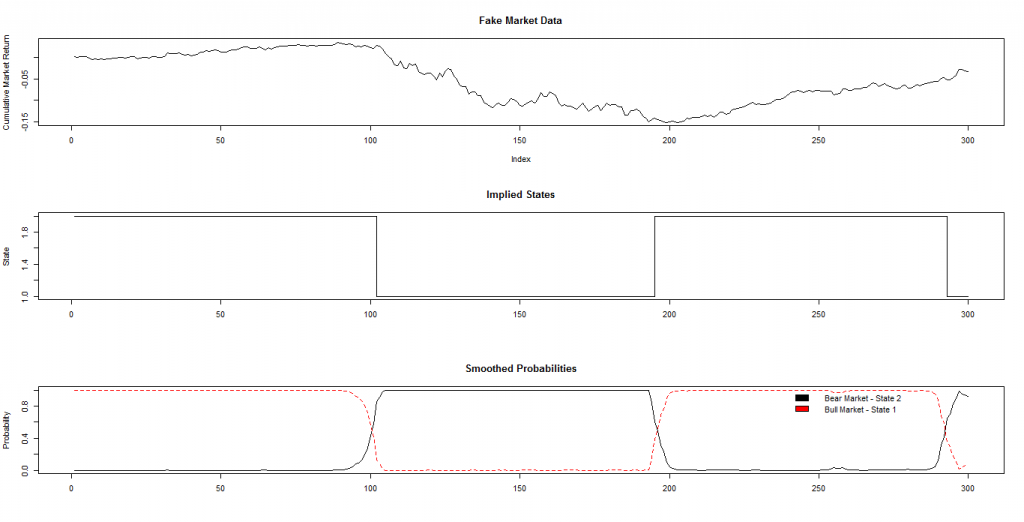
Для обучения модели будем использовать исходные данные, полученные симуляцией из нормального статистического распределения N(mu,sigma), где mu — медиана, sigma — среднеквадратичное отклонение. Распознавание будем производить для двух режимов — бычьего (bull) рынка, на котором наблюдается восходящий тренд и медвежьего (bear) рынка, на котором тренд нисходящий. Соответственно, сгенерируем приращение значений из двух нормальных распределений - N (mu.Bull,sigma.Bull) и N(mu.Bear,sigma.Bear). На рисунке показан результат такой генерации на 300 наблюдений, 100 первых из которых получены из бычьего распределения, 100 вторых — из медвежьего и 100 последних — из бычьего с другими параметрами mu и sigma (каждое приращение будем считать дневным):
( Читать дальше )
Модель скрытых состояний Маркова. Часть 1
- 12 мая 2015, 14:35
- |
В данном цикле статей начинаем рассматривать модель Маркова, которая находит применение в задачах классификации состояния рынка и используется во многих биржевых роботах. Статьи основаны на постах, опубликованных в блоге Gekko Quant. Также будет рассмотрены практические алгоритмы на финансовых рынках. Код в цикле приведен на языке R. Вначале будет много теории, ее надо хотя бы попробовать понять, затем разберем практические примеры.
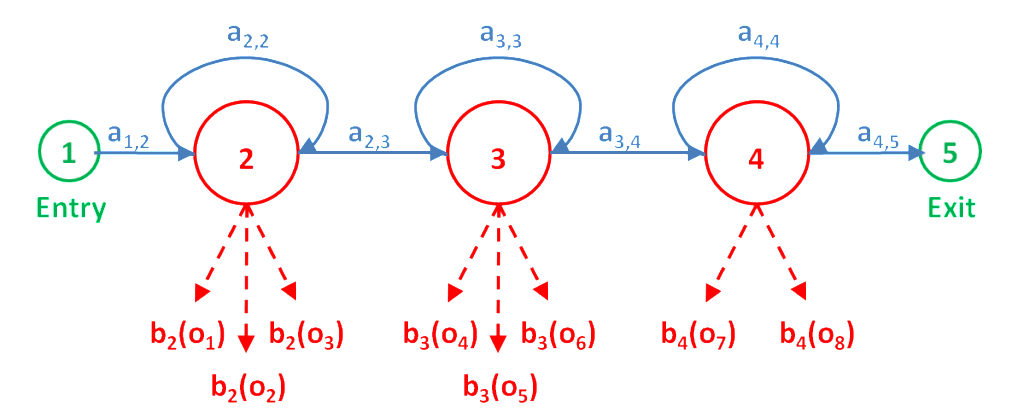
Рабочая среда распознавания основных паттернов.
Рассмотрим набор признаков O, полученный из набора данных d и класс w, обозначающий наиболее подходящий класс для O:
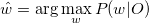
( Читать дальше )
Линейная регрессия с использованием фильтра Калмана
- 23 апреля 2015, 10:12
- |
Линейная регрессия часто используется для вычисления пропорции хеджирования в парном трейдинге. В идеальной ситуации коэффициенты этой регрессии — наклон линии регрессии и свободный член (пересечение) остаются всегда постоянными. Однако в реальности все, конечно, не так радужно, и значения этих параметров постоянно меняются во времени. Как правильно вычислять коэффициенты регрессии, чтобы избежать подгонки к текущей ситуации, рассматривается в статье "Online Linear Regression using a Kalman Filter". Для этой цели в данной публикации используется фильтр Калмана.
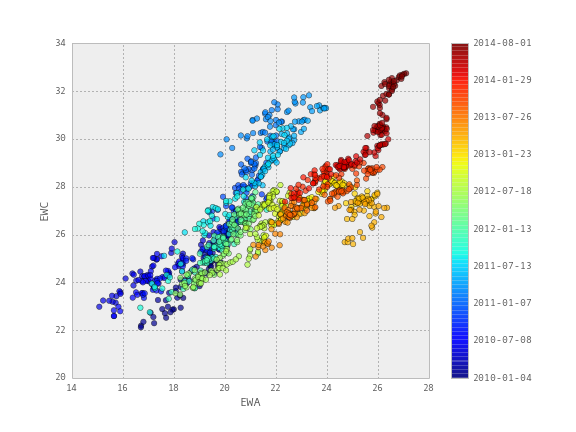
Для тестирования берутся исторические цены закрытия двух биржевых фондов ETF — австралийского EWA и канадского EWC с 2010 по 2014 год. Динамика цен этих фондов показывает взаимосвязь, что продемонстрировано на диаграмме рассеивания в заглавии поста. Однако по этому же графику видно, что эту взаимосвязь невозможно описать с помощью линейной регрессии с постоянными коэффициентами.
( Читать дальше )
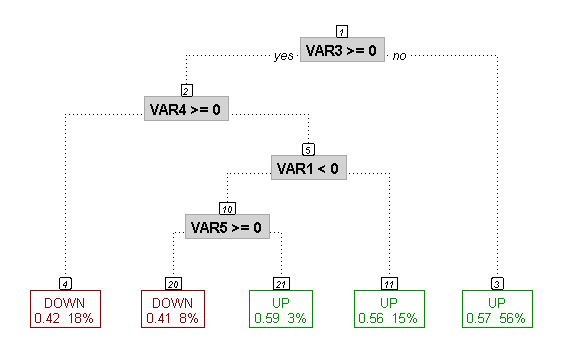
Использование CART в предсказании направления рынка
- 21 апреля 2015, 10:19
- |
Интересный подход к предсказанию направления рынка рассмотрен в статье "Using CART for Stock Market Forecasting". Для того, чтобы предугадать движение цены на недельном отрезке используется техника под названием CART (Classification And Regression Trees) — построение классификационного графа (дерева) с целью предсказать значение целевой характеристики (цены) на основании набора объясняющих переменных. CART находит применение во многих областях науки и техники, но применим и в торговле, так как обладает набором свойств, хорошо подходящими для этой цели:
- может применяться при любом типе статистического распределения
- может применяться как для линейных, так и нелинейных зависимостей
- устойчив к событиям, выходящим за рамки статистических распределений
Для построения дерева автор использует библиотеку языка R, вычисляющую рекурсивное разделение (Recursive Partitioning) rpart.
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал