Чтобы стабильно расти в трейдинге, надо всегда быть непогрешимым. Каждый день только в рамках плана и никак иначе. Один раз стоит оступиться, на рынке фьючерсов можно слить все или почти всё. Слить всё — означает обанкротить свой бизнес.

Трейдер-бизнесмен понимает, что его капитал — это и основа его бизнеса, его цель и источник его основного дохода.  
Трейдер-любитель живет за счет зарплаты или других доходов и знает, что если ошибется, то не умрет с голоду, а со временем сможет открыть новый счет и снова будет торговать. 

Любителю сложно будет соблюдать правила каждый день. И результат его будет непостоянен.
Профессионал понимает, что нарушить один правила, — это может быть конец.
Нарушить всего один раз правила для профессионала — это пустить себе пулю в голову.

Этот материал накапливался годами. Напряженная торговая практика заставляла искать ответы на вопрос: «Ну почему у меня ничего не получается?».

Ответ мог быть только один — послушай мнение людей, которые добились успеха. Здесь из разных источников собраны правила, мысли, взгляды настоящих профессионалов.

1. Рассматривайте потери как плату за обучение.

2. Никогда не входите в рынок, если потери превышают установленный лимит.

3. Пропускать торговый сигнал очень плохо — можно упустить большую прибыль. Необходимо использовать каждый торговый сигнал. Против потерь есть защита — стоп-ордер, а против упущенной возможности — нет.

4. Необходимо правильно и всегда устанавливать внутри торговый стоп-ордер.

5. Торговая система всегда должна быть разработана и адаптирована под конкретную личность.

6. Любая торговая система имеет период серии потерь.

7. Сосредоточьтесь на процессе торговли, а не на результате.

( Читать дальше )

Скальпер.
Вараинты входа в позицию:
1.Пробой, отбой.
2.Повадыри пошли.
3.Мамка взлетела.
4.Оо плотность, вхожу.
5.Круглое число.
6.Большущий сайз.
7.На откате заберу.
8.Отбой от тренда.
9.Пробой консолидации.
10.Блин не там вошел, отобъю.
11.Выход из треугольника.
12.Медвежье поглашение, войду.
13.Фух, отбил… опа новости.
14.Двухсотую не пробили)), шорт.

Интрадейщик.
1.Ретест дня.
2.Закрепление под/над уровнем.
3.Проторгованная база, есть куда стоп спрятать.
4.Круглый уровень.
5.Ложный пробой.
6.Двойное дно.
7.Бля, выбило… перезайду.

Инветстор.
1.Слияние и поглащения.
2.Ближущиеся банкротства и перспективные проекты.
3.3х и 5ти летние минимумы.
4.Фундаментальные данные с хреновыми годовыми показателями.
5.Влажусь в 5ть стартапов, кто то выстрелит. 

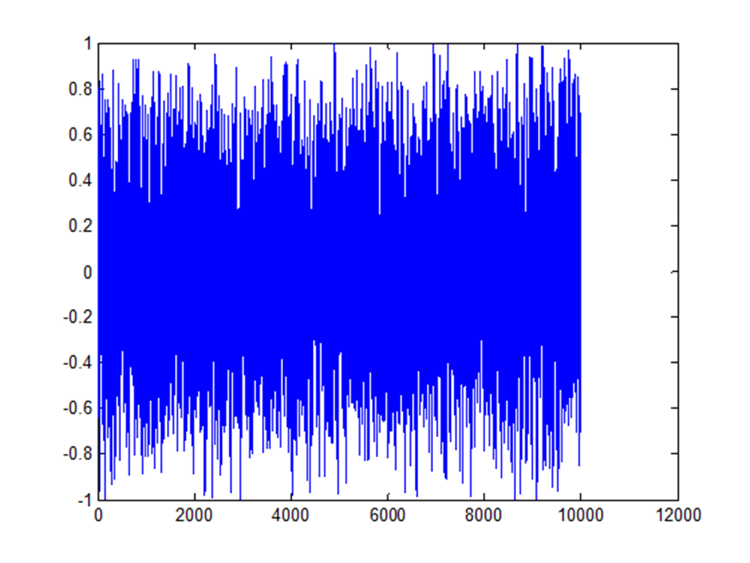
Насколько успешным может быть применение индикатора токсичности потока ордеров VPIN в трейдинге? А если попробовать соединить его с моделью скрытых состояний Маркова? Пример такой стратегии приводит Dr Jonathan Kinlay в своем блоге. Напоминаю, что всю теорию по расчету VPIN вы сможете найти на моем сайте здесь, а по модели Маркова — здесь.

Для наших целей интерес представляет однопериодный знаковый VPIN. Он принимает значения от -1 до 1, в зависимости от пропорции между покупками и продажами за один период t — см. график в заглавии статьи.

Мы предполагаем, что приращение цены актива имеет сильную зависимость от значения VPIN. Например, в тестах фьючерса ES, мы увидели, что изменение средней цены от одного объемного пакета ( см. теорию VPIN) до следующего высококоррелировано со значением VPIN в предыдущем пакете с коэффициентом 0,5. Другими словами, участники рынка, предоставляющие ликвидность, будут обновлять свои ордера в направлении, которое прямо связано с направлением и интенсивностью потока токсичности.

( Читать дальше )

Ребят подскажите популярные наши и зарубежные форумы, сообщества на тематику: бизнес, инвестиции, форекс, биржа.
Пока нашел следующие:

• h2t.ru
• investazy.com
• elitetrader.com
• trade2win.com
• tradingview.com
• ну и smart-lab.ru  
• howtotrade.ru (форум А.Г.)
• bigmiketrading.com
• seekingalpha.com
• investorplace.com
• zacks.com
• fool.com
• mt5.com/ru
• investcafe.ru
• investfunds.ru
• 2stocks.ru
• finanz.ru
• zerohedge.com
• traderkingdom.com

( Читать дальше )

Был у меня давно граальный алгоритм для fRTS. Работал в плюс без подстроек годами, но вот в 2015 году что-то случилось… как не тужся, но параметры алгоритма оптимизированные на предыдущих годах к 2015 году не подходят:

 

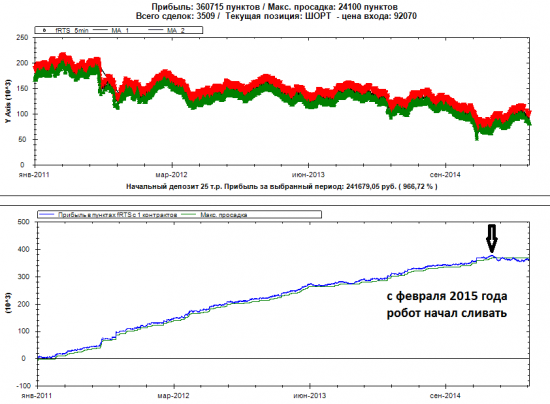
фишка была в том, что сам алгоритм примитивен до опупения… но работал..

вся логика — 5 строк кода 

if (pr > max) { max = pr; ind = 1; }   // — если обновляем максимум то в лонг
if (pr < min) { min  = pr; ind = -1; }  // — если обновляем минимум то в шорт

max -= k2;   // максимум плавно опускаем каждую 5-минутку
min += k3;  // минимум плавно поднимаем каждую 5-минутку

if ((ind == 1) && (pr < max- stop_long)) ind = 0;  // если цена ниже максимума на размер стопа и мы лонге — выход кеш

( Читать дальше )

Формация определенна мною за 2-х летний период в трейдинге. Как по мне так она очень даже работающая. И живет очень долго))
За 2 года канечно было много найденно закономерностей, формаций и тому подобных вещей.
Ну канечно как у всех они умирали сразу, короче долго не жили.))

Но эта фармация имеет право на жизнь, ее Я тестировал на истории с 11 года по сей день все работает. Добавте каких то фильтров или уровней, по тренду или еще что то, будет очень даже гуд.
Посмотрите на каком ТФ меньше шумов, и т.г.д))
Канечно Я в законамерности на рынки не верю, но эта мне покая не дала))
Надеюсь кому помогу, этой статьей))
И своей идеей))))
 

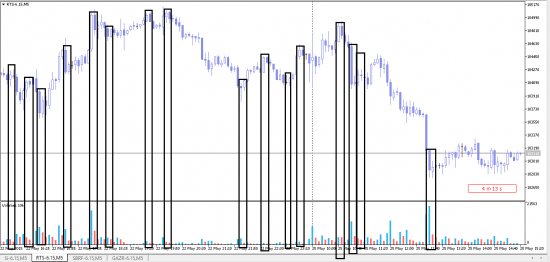
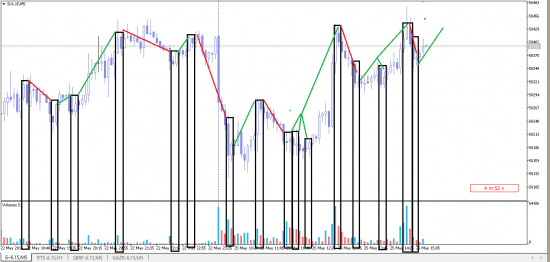
( Читать дальше )

Послушал бесплатный вебинар Максима Свиридова. Решил протестировать его идеи, что вход не так важен, как РМ.



( Читать дальше )

В этой части рассмотрим обучение модели скрытых состояний Маркова на языке R. В прошлых статьях мы изучили математическую основу модели, которая воплощена в библиотеке RHmm. Есть два способа распознавания режимов с помощью модели Маркова, первый — использование одной модели, каждое состояние которой отражает режим, в каком находится рынок. Второй способ подразумевает построение нескольких моделей, каждая из которых создана для одного режима, задача состоит в том, чтобы выбрать ту модель, которая генерирует данные, наиболее соответствующие текущему состоянию рынка. Рассмотрим оба эти способа.

 

Метод первый — одна модель с несколькими состояниями.

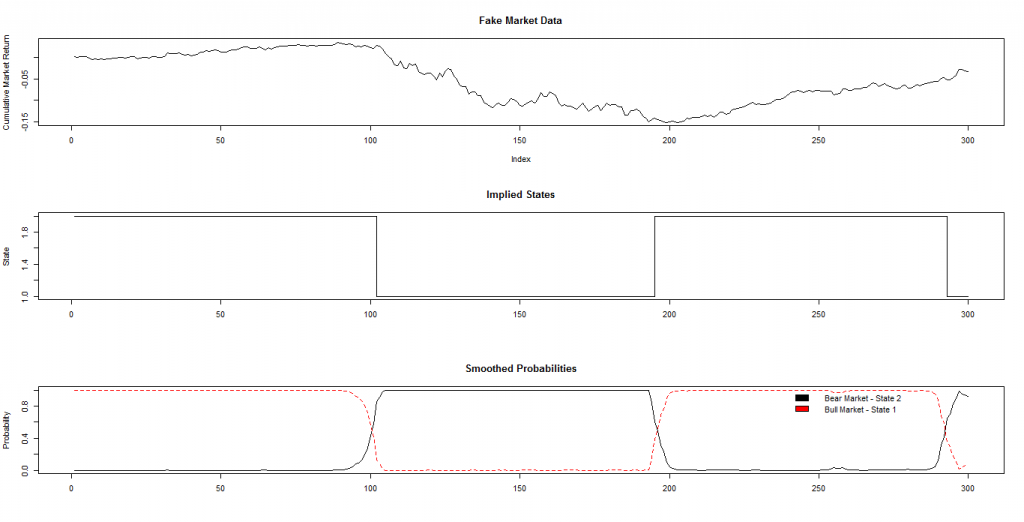
Для обучения модели будем использовать исходные данные, полученные симуляцией из нормального статистического распределения N(mu,sigma), где mu — медиана, sigma — среднеквадратичное отклонение. Распознавание будем производить для двух режимов — бычьего (bull) рынка, на котором наблюдается восходящий тренд и медвежьего (bear) рынка, на котором тренд нисходящий. Соответственно, сгенерируем приращение значений из двух нормальных распределений - N (mu.Bull,sigma.Bull) и N(mu.Bear,sigma.Bear). На рисунке показан результат такой генерации на 300 наблюдений, 100 первых из которых получены из бычьего распределения, 100 вторых — из медвежьего и 100 последних — из бычьего с другими параметрами mu и sigma (каждое приращение будем считать дневным):

( Читать дальше )

Доброе утро, коллеги! Прямая трансляция торговли на сегодня: 18.05.2015
Начало проекта тут.



Всем удачного дня и тёплого месяца мая!))