Блог им. SergeyAlekseev_1b0
Узнайте как можно заработать 43% за год. Часть 2: Как посчитать стоимость ОФЗ и потенциальную доходность
- 02 октября 2024, 20:03
- |
В прошлой статье я показал как выбираю ОФЗ, наилучшим образом подходящую под мои цели и задачи. Расчет проводился на примере ОФЗ ПД 26240.
Полностью со статьей можно ознакомиться здесь.
Вы научитесь учитывать такие параметры, как ставка доходности, оставшиеся купоны и накопленный купонный доход (НКД), а также сможете проверить свои расчеты на реальных данных.
Кроме того, еще раз оценим, как меняется доходность облигации в зависимости от изменения ставки доходности через год и как можно прогнозировать ваши риски.
Итак, приступим.
 Как посчитать стоимость ОФЗ и потенциальную доходность
Как посчитать стоимость ОФЗ и потенциальную доходностьРассчитываем стоимость ОФЗ
Напомню, что основным фактором выбора является возможная потенциальная доходность от владения той или иной ОФЗ.
Я считаю Ртек, как цена последней сделки + НКД
Pбуд считается на окне в год и два года с учетом:
- выплаченных купонов за время владения (год или два)
- оставшейся структуры выплат (купонов и номинала) и какой-то новой ставкой доходности.
- накопленного НКД
Потенциальная доходность считается по формуле
Dпот = Рбуд-Ртек — потенциальная доходность в абсолютном выражении, в рублях
Dпот% = ((Рбуд-Ртек)/Рбуд)*100% — относительная доходность, в процентах
Dпот%год = Dпот%*(365/Тинв) (Тинв — время инвестиций в днях) — относительная доходность в процентах годовых. Позволяет сравнивать разные облигации с неравными сроками инвестирования.
Считая потенциальные доходности по всему множеству ОФЗ ПД, их можно сравнить между собой и выбрать лучшую по потенциальной доходности. Или можно сделать выбор по каким-то другим характеристикам, доступным в таблице с расчетами. Впрочем, об этом более подробно я проговорил в прошлой статье.
Статья получила некую популярность, многие попросили прислать расчет.
Обратная связь была положительной, таблица с расчетами понятна, идея понятна. Правда почему-то все комментарии прилетели только в моем ТГ канале и личных сообщениях.
Кстати, если кому-то интересно посмотреть эти расчеты, пишите по ссылке в телеграм «хочу расчет» — вышлю актуальный расчет.
Но были и другие комментарии. Эти комментарии можно разделить на две части:
Первая часть:
идея понятна, но как это посчитать самому, как эти вычисления сделать в Excel.
Вторая часть:
формула притянута за уши, автор не понимает основ ценообразования, формула не верна, я никогда не слышал про такую формулу, она не работает, вы пытаетесь спрогнозировать ставку ЦБ, вам не удастся это сделать.
На каком-то этапе я решил, что спорить бесполезно и решил написать продолжение статьи и показать, как сделать подобный расчет в Excel “на коленках” (знаю, что это можно сделать более компактно, но для наглядности этот подход будет лучше) и заодно показать, что расчеты совпадают с биржевыми ценами.
Формула для расчета цены облигацииP — цена облигации
К — размер купонов
R — ставка доходности облигации
Т — время инвестирования
Я утверждаю, что если в правую часть уравнения подставить все данные, то получится вычислить цену облигации, по которой она сейчас торгуется на бирже.
Буду приводить пример расчета на основе той же ОФЗ ПД 26240.
На 02.10.24 данные такие (они автоматически подгружаются из QUIK в Excel):
Цена последней сделки — 536,76 руб.
Ставка доходности — 16,37%
НКД — 9,59 руб. (Накопленный Купонный Доход).
Размер купона — 34,9 руб. (купон у этой облигации будет платиться 2 раза в год, т.е. годовой купон 69,8 руб.)
Дней до погашения — 4319, это 11,83 года.
Дюрация — 2429 дней
В первую очередь я считаю оставшееся количество купонов до погашения. Т.е. сколько целых купонов я получу, если буду держать облигацию до погашения.
Дней до погашения — 4319
Длительность купона 182 дня.
Делим дней до погашения на длительность купона — 4319/182, получаем чиселку 23,73. Округляем эту чиселку вверх до целого и получаем 24.
Это значит, что до погашения облигации осталось получить 24 купона.
В соответствии с вышеуказанной формулой, получается, что нужно посчитать 24 слагаемых.
Для этого в таблице создаем 24 строчки и их нумеруем.
Далее нам известно количество дней до погашения — 4319 (соответствует 24 строке) и длительность купона -182 дня.
Если из количества дней до погашения построчно вычитать длительность купона, то можно посчитать сколько дней осталось до выплаты каждого купона.
Получается таблица следующего вида:

Количество дней до выплаты каждого купона
Получается, что до ближайшей выплаты купона осталось 133 дня, до выплаты последнего купона и номинала (до погашения) - 4319 дней.
Для вычислений по формуле мне нужны сроки инвестирования по каждому купону.
Для этого считаю количество дней возможных для реинвестирования по каждому купону. Для этого, построчно из дней до погашения вычитаем дни, оставшиеся до выплаты каждого купона.
Т.е. первый ближайший купон (первая строчка) я получу через 133 дня. Я знаю, что полное погашение облигации через 4319 дня. Это значит, что купон, который я получу через 133 дня, можно реинвестировать в эту же облигацию на 4186 дней.
Получается таблица следующего вида:

Срок реинвестирования для каждой выплаты купонов
Последний купон и номинал я получу через 4319 дней (т.е. при погашении облигации) и останется 0 дней для реинвестирования.
Далее, все по формуле, считаю каждое слагаемое формулы построчно.
Я дисконтирую будущий денежный поток в виде купона к текущему моменту с учетом текущей ставки доходности облигации.
Для этого вычитаю из размера купона - НКД, накопленный на текущий момент, и делю получившееся значение на ставку доходности, возведенную в степень, значение которой вычисляется как количество дней возможных для реинвестирования, деленных на 365 дней
Т.е. Р1 = (Размер купона1 — НКД)/(1+ставка доходности облигации)^(Дней реинвестирования/365)
Р1=(34,90-9,59)/(100+16,37%)^(4186/365) = 4,448 руб.
Т.е. с помощью ставки доходности R и срока T, я будущий денежный поток привожу к текущему.
И так вычисляем по каждой строке — по каждому купону. Получившиеся значения суммируем. Получается такая табличка:

Дисконтирование купонов
Получается, что цена облигации должна составлять 536,757 руб, назовем эту переменную Ртек.расч.
Ртек.расч. = 536,757 руб.
А что с фактической ценой -
Ртек.факт. = 536,76 руб. — ее подгрузили из QUIK, как последнюю цену сделки.
Ртек.факт.-Ртек.расч.= 0,003 руб
Т.е. я ошибся в расчетах на 0,3 копейки, текущая фактическая цена облигации на 0,001% больше того значения, которое я получил по формуле.
Я считаю, что это довольно маленькая погрешность, которой можно пренебречь.
Формула верная, расчетная цена облигации совпадает с фактической!
Сделаем еще ряд проверок.
Для этого посчитаю Рбуд на момент погашения с учетом реинвестирования всех купонов по существующей ставке доходности.
умножаем на

получаем
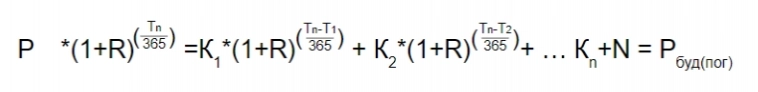
Таким образом, считаем доход от каждого полученного купона с учетом дней оставшихся для реинвестирования (дней до погашения от каждого выплаченного купона) с учетом существующей ставки доходности.
Рбуд1 = (Размер купона — НКД)*(100+16,37%)^(4186/365)=144,009 руб.
Т.е. первый ближайший выплаченный купон за минусом уплаченного продавцу НКД (34,90-9,59=25,31 руб.) будет стоить на момент погашения облигации 144,009 руб. если удастся этот купон реинвестировать под текущую ставку доходности этой облигации.
Суммируя значения по всем купонам получаю Рбуд облигации с учетом реинвестиции всех купонов по текущей ставке доходности.
Получается так:

Реинвестиция купонов
Получается, что будущая цена облигации с учетом реинвестиции купонов будет 3228,36 руб.
Dпот= Рбуд — Pтек = 3228,36 — 546,35 = 2682,01 руб
Dпот%=490,89%
Dпот%год= 41,48% годовых
Да! Такая некислая доходность получается у этой облигации, если все купоны до погашения удастся реинвестировать под ту ставку доходности, которая есть сейчас — это 16,37%.
Теперь примерно представляете, как будет пухнуть денежная масса, если ЦБ не будет снижать ключевую ставку.
Я эту доходность не беру ни для каких рассуждений т.к. какая ставка будет в будущем — мы не знаем, и надеяться на то, что все купоны можно будет реинвестировать по этой ставке нельзя. Ставка в будущем может быть меньше, а может быть и больше.
Гораздо информативней на мой взгляд считать Рбуд без учета реинвестирования купонов (пассивный доход), считая, что это минимально возможная доходность от владения этой облигацией.
Рбуд = (номинал+24 купона) = 1000+24*34,9=1837,6 руб.
Ртек =546,35 руб.
Dпот= Рбуд-Pтек = 1837,6 — 546,35 = 1291,25 руб
Dпот%=236,34%
Dпот%год= 19,97 % годовых
Вернемся к проверке. Есть более простая и понятная формула

Считаем будущую цену облигации
Чтобы понять будущую стоимость актива, нужно текущую стоимость умножить на ставку доходности.
Например, положили вы на депозит с доходностью 20% годовых сумму в размере 100 000 руб. Через год - Рбуд вашего депозита будет 120 000 руб.
Соответственно, чтобы понять какая Рбуд у облигации, нужно текущую цену облигации умножить на ставку доходности, возведенную в степень (время инвестирования в днях, деленное на количество дней в году)
Pбуд.расч. = 536,76*(100%+16,37%)^(4319/365) = 3227,50 руб.
Ранее, в таблице, путем построчного суммирования значений с учетом реинвестирования купона получилось 3228,36 руб. Погрешность в 0,86 руб. или 0,026% — считаю ее незначительной. Т.е. все сходится.
Из этой же формулы можно вычислить Ртек.

Формула для расчета цены облигации
В нашем случае это:
Ртек.расч = 3228,36/(100+16,37%)^(4319/365)=536,89 руб.
Ранее, в таблице, путем построчного суммирования значений с учетом дисконтирования купонов получилось 536,75 руб. Погрешность в -0,14 руб. или -0,026% - считаю ее незначительной. Т.е. все сходится.
Формула для расчета цены облигации
Именно по этой формуле считается стоимость всех облигаций.
Покупатели и продавцы торгуют между собой цену облигации, это происходит в каждый момент времени. Эта цена — цена последней сделки, она известна в любой момент времени.
Структура, размер, сроки выплат купонов и номинала заранее известны, они прописаны в проспекте облигации, эти значения можно взять из таблицы параметров в QUIK.
Текущая цена известна, будущее с точки зрения будущих платежей известно, программе остается только путем подбора подставить в это уравнение правильную ставку доходности и обе части уравнения будут равны.
Т.е. выставляя заявку в стакане на покупку облигации по конкретной цене, программа вам по этой формуле пересчитывает и говорит, под какую ставку доходности вы сейчас собираетесь купить облигацию.
Если все так, то что нам мешает посчитать цену облигации через год.
Что через год изменится?
Возможно ставка изменится, а возможно нет. Поэтому я рассматриваю различные варианты ставок через год (в прошлой статье я подробно описал каждый вариант).
Точно изменится структура выплат — на два купона у этой облигации станет меньше.
Так и считаем Рбуд, которая будет равняться Ртек этой облигации, но через год с оставшейся структурой выплат и с какой-то другой ставкой, например с 12%.
В таблице делаем тоже самое, только не забываем убрать из вычислений 2 купона и подставить новое значение ставки доходности.
Получается так:

Рассчитываем параметры облигации через год
Далее вычисляем потенциальную доходность от владения этой облигацией.
Dпот = Рбуд (цена + НКД +2 купона) — Pтек (цена +НКД) = 796,65 — 546,35 = =250,30 руб.
Dпот% = 45,81%
Потенциальная доходность даже подросла (по сравнению с потенциальной доходностью, рассчитанной в прошлой статье) за счет того, что цена облигации немного припала.
В облигациях в этом смысле вообще все хорошо. При любом изменении рынка, растет либо цена облигации, либо доходность.
Делаем выводы
Я не пытаюсь угадать какой будет ключевая ставка через год, я не пытаюсь посчитать насколько ставка доходности облигаций коррелирует с ключевой ставкой ЦБ или RUONIA. Хотя, что-то мне подсказывает, что вектор у них направлен в одну сторону)
Я просто просчитываю свои риски при различных вариантах ставок через год. Сколько будет стоить эта облигация при ставке доходности в 20%, 12% или 16%, как сейчас, если ставка не изменится.
В расчетах в первой части статьи на примере ОФЗ ПД 26240 получилось, что если:
- ставка вырастет на 4%, до 20%, то я за год потеряю 3,7%
- ставка упадет на 4%, до 12%, то я за год заработаю 43%
Впрочем все подробности можно прочитать в первой части статьи. Здесь.
Если вам стало интересно и вы хотите получить расчет по всему множеству длинных ОФЗ ПД (постоянный доход), я готов с вами поделиться моей таблицей.
Для этого нужно перейти по ссылке в телеграмм и написать “хочу расчет” (не волнуйтесь, это бесплатно), в ответ вы получите инструкцию, как получить таблицу с расчетами по всему множеству длинных ОФЗ ПД.
Спасибо, что дочитали до конца, надеюсь, мне удалось донести до вас несколько толковых мыслей и навести на правильные размышления.
Подробнее о инвестициях в финансовые инструменты на моем канале в Телеграм.
теги блога Будни опционщика и инвестора
- IMOEX
- акции
- бизнес
- Брокер
- валюта
- вклады
- волатильность
- гамма опциона
- Греки
- дельта
- дельта-нейтральность
- дельта-хеджирование
- депозит
- деривативы
- долг
- доходности облигаций
- доходность акций
- доходность облигаций
- дюрация
- инвестиции
- инвестор
- Индекс МБ
- инфляция
- инфляция в России
- ключевая процентная ставка
- ключевая ставка
- Ключевая ставка ЦБ РФ
- комиссии
- коннектор
- ликвидность
- ликвидность опционов
- направленное движение
- недвижимость
- Облигации
- облигации офз
- опцион
- опционная позиция
- опционная стратегия
- опционы
- опционы волатильность
- офз
- ОФЗ ПД
- ОФЗ с переменным купоном
- покупка волатильности
- портфель
- портфель акций
- продажа волатильности
- процентная ставка
- риск
- софт
- справедливая стоимость
- срочный рынок
- ставка рефинансирования
- торговля волатильностью
- трейдинг
- тренд
- улыбка волатильности
- управление опционной позицией
- управление позицией
- Управление портфелем
- флоатеры
- фьючерс
- фьючерс MIX
- фьючерс РТС
- ФЬЮЧЕРСЫ
- Фьючерсы и Опционы
- хедж
- хеджер
- хеджирование рисков
- ЦБ РФ
- ценообразование на рынке
- эксперимент






















Пользователь разрешил комментарии только друзьям.