Толстые хвосты и эмпирические распределения. Продолжение

Продолжаю тему, поднятую в статье «Толстые хвосты и эмпирические распределения». Напоминаю, в материале рассматривался вопрос, как влияют толстые хвосты распределения цены базового актива на появление улыбки волатильности. В представленной модели фьючерс РТС каждый день прыгает на величину, случайно выбранную из ряда его ежедневных приращений в прошлом. Ранее были показаны результаты модели для 100 шагов движения цены. К ним мы еще вернемся, а пока рассмотрим, что происходит при небольшом количестве шагов модели. В этом случае, Центральная Предельная Теорема только начинает работать, и толстые хвосты разворачиваются во всей своей павлиньей красе.




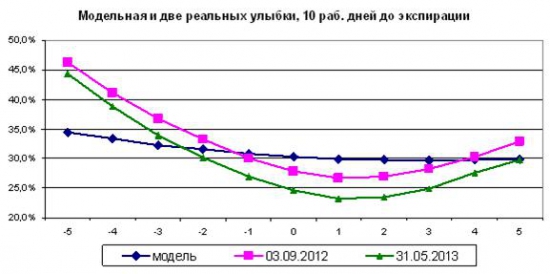
Выше представлена модельная улыбка за 10 дней и две реальных кривых волатильности опционов с аналогичным сроком жизни. Как и раньше, в модели введена поправка на тренд. По оси Х номер страйка от центрального, графики совмещены по горизонтали. 




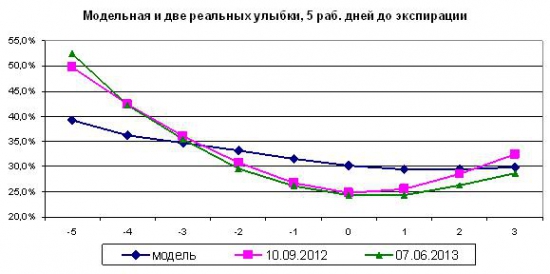
А здесь нам улыбается график модельной пятидневной кривой в сравнении с двумя реальными улыбками. Мы видим, что модель действительно порождает улыбку на коротких интервалах времени. Любопытно, что донышко модельной кривой находится справа от центрального страйка, а не совпадает с ним. Такое явление часто наблюдается и на практике. Тем не менее, очевидно, что наклон модельной кривой значительно ниже, чем мы наблюдаем в жизни, что не позволяет использовать модель для точного предсказания улыбки на коротких сроках. Наличие толстых хвостов оказывается недостаточным условием для формирования улыбки волатильности, адекватной реальности. 

Чем выше срок до экспирации, тем более пологой становится кривая волатильности. Посмотрим, как быстро сглаживается кривая на примере третьего по счету от денег страйка. Начальная точка модели 157090 п. Модельная волатильность базового актива в годовом выражении 30,49%.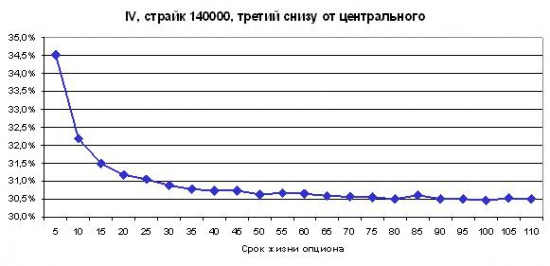
Мы видим, что с ростом шагов волатильность стремится к целевому уровню 30,49%. В прошлой статье я разместил график итогов модели для 100 шагов. Должен признать, что Андрей Агапов в своем комментарии к моей предыдущей статье был прав, и слабенький наклон все-таки существует, что подтвердило более точное моделирование с увеличенным числом повторений для большего числа страйков. 




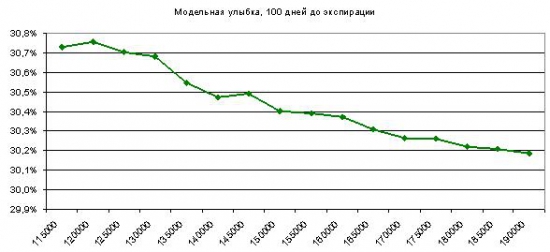
Так средняя разница по волатильности между соседними страйками вблизи денег составляет 0,05%. Слабые следы улыбки наблюдаются даже для 200 шагов модели, разница между страйками около 0,01%. Таким образом, второй вывод предыдущей статьи не слишком точен: улыбку зафиксировать можно, хотя она и далека от реальности.

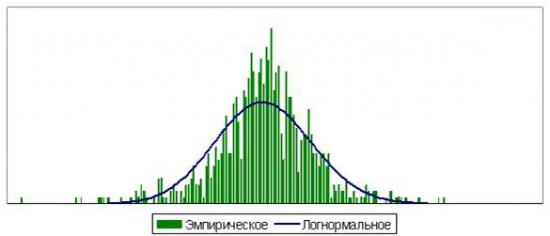
Интересно, что улыбка превратилась в ухмылку, и это характерно для большого числа шагов. Думаю, это связано с тем, что форма эмпирического распределения слева и справа отличаются. Слева график немного более пологий, его хвост длиннее и толще. Возможно, для малого количества шагов важна отдаленная часть хвоста, а для для длинных периодов большее значение имеет средняя часть хвоста, которая слабее выражена справа. На графике эмпирическое распределение, приведенное экспонентой к ежедневным приращениям. 


Я намеренно не касался случаев непостоянной волатильности, чтобы отделить эффект толстых хвостов от эффекта переменной волатильности. Действительно, модели с непостоянной волатильностью рисуют улыбки, похожие на реально существующие. Другим эффектом переменной волатильности являются толстые хвосты распределения ежедневных приращений. То есть мы имеем два следствия одного явления, и нельзя одно из этих следствий назвать причиной другого. Так же как нельзя назвать причиной быстрого роста грибов лужи на асфальте.

Выводы
Толстые хвосты эмпирических распределений сами по себе не могут объяснить возникновение улыбок волатильности, наблюдаемых на практике. Улыбки волатильности, порождаемые только эффектом толстых хвостов имеют существенно меньший наклон, чем наблюдаемые в жизни кривые. С ростом числа шагов рассмотренной модели наклон улыбок становится все слабее, но не исчезает полностью. 

P.S. Несколько технических пояснений к предыдущей статье
Мне хотелось бы остановится подробнее на том, что значит избавиться от тренда в модели. Недостаточно выбрать конечную цену исторического ряда логарифмов приращений цены равную начальной цене. В этом случае как раз остается положительный тренд, искажающий цены опционов. Предложенный мной способ состоит в следующем.

Во-первых, если конечная цена не совпадает с начальной, следует отнять среднее ряда из каждого его члена.
Во-вторых, из каждого члена ряда нужно вычесть выражение (σ* σ /2)*(T-t). Здесь σ – волатильность ряда в годовом выражении, (T-t) – период времени, соответствующий одному приращению. Например, если период – один рабочий день, то (T-t) = 1/250. Если  σ – просто СКО ряда, то умножать на (T-t) не нужно.

Замечу, что после исключения тренда, матожидание S(T) окажется равно S(0), но матожидание Ln(S(T)) — Ln(S(0)) будет -(σ* σ /2)*(T-t). Как так получается? Просто операция матожидания не переносится внутрь логарифма. Кроме того, для цен путов и коллов, как заметил Gusan должен выполняться пут-колл паритет.