SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. broker25
Heston, Lognormal, Lewis, SABR and CEV
- 15 августа 2014, 14:51
- |
Какая модель движения цены позволяет построить улыбку, наиболее близкую к рыночной?
Рассмотрим простой подход к выбору наилучшего метода.
Определение моделей
Для начала определим модели рынка.
a) Heston, Lognormal и Lewis.
В общем виде модель выглядит так.
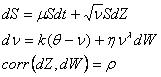
При λ = 0.5 получаем метод Хестона,
λ = 1 соответствует методу Lognormal,
λ = 1.5 соответствует методу Lewis’s 3/2.
Принимаем тренд равным нулю: μ = 0.
Неизвестные параметры:
θ — средняя долгосрочная волатильность;
η — vol of vol;
k > 0 - скорость сходимости текущей волатильности к средней;
ρ — коэффициент корреляции волатильности и БА;
б) Модель SABR
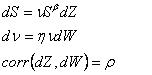
Неизвестные параметры:
0 ≤ β ≤ 1 ;
η ≥ 0 — vol of vol;
ρ — коэффициент корреляции волатильности и БА.
в) Модель CEV
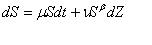
Неизвестен неотрицательный параметр β.
В этой модели нет стохастической волатильности.
Принимаем тренд равным нулю: μ = 0.
г) Naïve. Добавим для сравнения простой «наивный» способ прогноза с фиксированной улыбкой на 1 день.
Волатильность каждого страйка предполагается равной волатильности того же страйка в предыдущий день.
Подбор параметров и прогноз
Оптимальные параметры модели находятся минимизацией функционала ошибки.
Разница рыночных и модельных цен опционов суммируется и дает функционал, который масштабируется для удобства восприятия.
Цены опционов для каждого набора параметров вычисляются по Монте-Карло.
Частные производные для градиентного спуска также вычисляются методом Монте-Карло.
Как ни странно, производные получаются достаточно стабильные.
Оптимальный набор параметров также стабилен для фиксированной даты, хотя отличается для разных дат.
В качестве входных данных для калибровки параметров берутся цены опционов на фьючерс РТС на закрытие рынка в течение 10 последовательных дней.
Проверка проводится на последующих 10 торговых днях.
Рассмотрено семь близких пересекающихся периодов для калибровки и семь периодов для проверки.
Все дни находятся в интервале от 17/09/10 до 01/11/10. Дата экспирации – 15/12/10.
Период до экспирации нельзя назвать коротким, что исключает искажения, связанные именно с близкими сроками.
Для прогноза улыбки на текущий день используется:
— оптимальные параметры,
— текущая цена фьючерса,
— волатильность центрального страйка на предыдущий день.
Сравнение моделей
В таблице ниже указана ошибка прогноза представленных моделей.
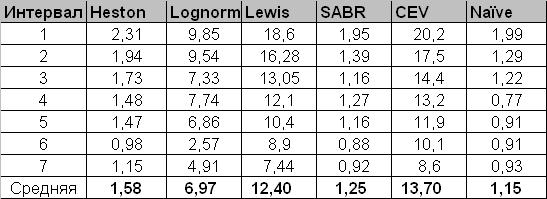
Как мы видим, в целом ни одна из моделей не превзошла простой наивный рыночный прогноз.
Метод SABR обогнал прочие модели рынка, и местами наивный прогноз. Heston показал близкие результаты. Остальные модели сильно отстали.
Посмотрим теперь на качество подгонки: какой метод дает минимальную погрешность своем оптимальном наборе параметров. Иначе говоря, какой способ позволяет нарисовать улыбку формы, наиболее близкой к рыночной. В табличке ниже указана минимальная ошибка во время обучения.
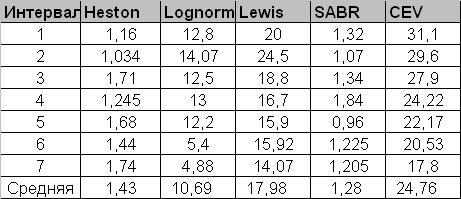
Мы видим, что и здесь SABR и Heston значительно опережают прочие модели.
Комментарии к расчетам
1. Данные выкладки не следует воспринимать как точный рэнкинг моделей. Здесь лишь предложен способ подобных расчетов. Тем не менее, значительное преимущество SABR и Heston говорит о смысле дальнейшей проработки именно этих методов.
2. Модели оказались в целом хуже простого наивного прогноза.
Это не говорит, однако, об их бесполезности. Есть много способов улучшения прогноза. Например:
— Взять другие моменты времени для калибровки;
— Увеличить или уменьшить число этих моментов;
— Изменить критерий и присваивать различным страйкам неодинаковые веса в функционале ошибки;
— Ввести в модель прыжки (jumps).
3. Метод Хестона дает коэффициент корреляции волатильности и БА от -0,7 до -0,5. В реальности, по моим расчетам он находится в пределах (-0,3 ; — 0,1). Замечу, что считать корреляцию нужно правильно: не по индексу волатильности, этот способ искажает ответ. Завышенный коэффициент корреляции говорит от том, что, возможно, модель не слишком реалистично передает динамику рынка, хотя и позволяет построить улыбку, похожую к рыночной. Можно задать границы для коэффициента, но это ухудшит качество подгонки.
4. Поиск оптимального решения по методу SABR занимает наибольшее время, и его приходится прекращать ограничением числа итераций. Очевидно, так происходит оттого, что параметр beta стремится к своему оптимуму — единице — и не может его достичь. В дальнейшем, в методе SABR я буду предполагать, что beta фиксирована и равна единице.
5. Ошибка методов Lognormal, Lewis и CEV на интервале проверки ниже, чем на интервале калибровки. Я связываю это с большей подвижностью улыбки на интервале калибровки.
Вывод:
Исследовано качество прогноза моделей Heston, Lognormal, Lewis, SABR и CEV для опционов на фьючерс РТС на заданном отрезке времени. Лучший результат показала модель SABR. Модель Heston показала близкие результаты. Остальные методы оказались намного хуже. Тем не менее, ни одна из моделей не превзошла простого наивного рыночного прогноза.
Рассмотрим простой подход к выбору наилучшего метода.
Определение моделей
Для начала определим модели рынка.
a) Heston, Lognormal и Lewis.
В общем виде модель выглядит так.
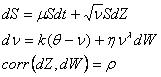
При λ = 0.5 получаем метод Хестона,
λ = 1 соответствует методу Lognormal,
λ = 1.5 соответствует методу Lewis’s 3/2.
Принимаем тренд равным нулю: μ = 0.
Неизвестные параметры:
θ — средняя долгосрочная волатильность;
η — vol of vol;
k > 0 - скорость сходимости текущей волатильности к средней;
ρ — коэффициент корреляции волатильности и БА;
б) Модель SABR
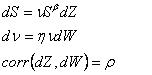
Неизвестные параметры:
0 ≤ β ≤ 1 ;
η ≥ 0 — vol of vol;
ρ — коэффициент корреляции волатильности и БА.
в) Модель CEV
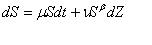
Неизвестен неотрицательный параметр β.
В этой модели нет стохастической волатильности.
Принимаем тренд равным нулю: μ = 0.
г) Naïve. Добавим для сравнения простой «наивный» способ прогноза с фиксированной улыбкой на 1 день.
Волатильность каждого страйка предполагается равной волатильности того же страйка в предыдущий день.
Подбор параметров и прогноз
Оптимальные параметры модели находятся минимизацией функционала ошибки.
Разница рыночных и модельных цен опционов суммируется и дает функционал, который масштабируется для удобства восприятия.
Цены опционов для каждого набора параметров вычисляются по Монте-Карло.
Частные производные для градиентного спуска также вычисляются методом Монте-Карло.
Как ни странно, производные получаются достаточно стабильные.
Оптимальный набор параметров также стабилен для фиксированной даты, хотя отличается для разных дат.
В качестве входных данных для калибровки параметров берутся цены опционов на фьючерс РТС на закрытие рынка в течение 10 последовательных дней.
Проверка проводится на последующих 10 торговых днях.
Рассмотрено семь близких пересекающихся периодов для калибровки и семь периодов для проверки.
Все дни находятся в интервале от 17/09/10 до 01/11/10. Дата экспирации – 15/12/10.
Период до экспирации нельзя назвать коротким, что исключает искажения, связанные именно с близкими сроками.
Для прогноза улыбки на текущий день используется:
— оптимальные параметры,
— текущая цена фьючерса,
— волатильность центрального страйка на предыдущий день.
Сравнение моделей
В таблице ниже указана ошибка прогноза представленных моделей.

Как мы видим, в целом ни одна из моделей не превзошла простой наивный рыночный прогноз.
Метод SABR обогнал прочие модели рынка, и местами наивный прогноз. Heston показал близкие результаты. Остальные модели сильно отстали.
Посмотрим теперь на качество подгонки: какой метод дает минимальную погрешность своем оптимальном наборе параметров. Иначе говоря, какой способ позволяет нарисовать улыбку формы, наиболее близкой к рыночной. В табличке ниже указана минимальная ошибка во время обучения.

Мы видим, что и здесь SABR и Heston значительно опережают прочие модели.
Комментарии к расчетам
1. Данные выкладки не следует воспринимать как точный рэнкинг моделей. Здесь лишь предложен способ подобных расчетов. Тем не менее, значительное преимущество SABR и Heston говорит о смысле дальнейшей проработки именно этих методов.
2. Модели оказались в целом хуже простого наивного прогноза.
Это не говорит, однако, об их бесполезности. Есть много способов улучшения прогноза. Например:
— Взять другие моменты времени для калибровки;
— Увеличить или уменьшить число этих моментов;
— Изменить критерий и присваивать различным страйкам неодинаковые веса в функционале ошибки;
— Ввести в модель прыжки (jumps).
3. Метод Хестона дает коэффициент корреляции волатильности и БА от -0,7 до -0,5. В реальности, по моим расчетам он находится в пределах (-0,3 ; — 0,1). Замечу, что считать корреляцию нужно правильно: не по индексу волатильности, этот способ искажает ответ. Завышенный коэффициент корреляции говорит от том, что, возможно, модель не слишком реалистично передает динамику рынка, хотя и позволяет построить улыбку, похожую к рыночной. Можно задать границы для коэффициента, но это ухудшит качество подгонки.
4. Поиск оптимального решения по методу SABR занимает наибольшее время, и его приходится прекращать ограничением числа итераций. Очевидно, так происходит оттого, что параметр beta стремится к своему оптимуму — единице — и не может его достичь. В дальнейшем, в методе SABR я буду предполагать, что beta фиксирована и равна единице.
5. Ошибка методов Lognormal, Lewis и CEV на интервале проверки ниже, чем на интервале калибровки. Я связываю это с большей подвижностью улыбки на интервале калибровки.
Вывод:
Исследовано качество прогноза моделей Heston, Lognormal, Lewis, SABR и CEV для опционов на фьючерс РТС на заданном отрезке времени. Лучший результат показала модель SABR. Модель Heston показала близкие результаты. Остальные методы оказались намного хуже. Тем не менее, ни одна из моделей не превзошла простого наивного рыночного прогноза.
теги блога broker25
- HV
- IV
- KZOS
- NKNC
- акции
- акции США
- алготрейдинг
- бабочка
- Брокер
- бэктестинг
- бюджет
- волатильность
- вор
- ВТБ
- второй эшелон
- газ
- газеты
- Газпром
- дельта-хеджирование
- дефицит бюджета
- дивиденды
- железный кондор
- здоровье трейдера
- зигзаг
- Индексы
- Историческая волатильность
- Казаньоргсинтез
- Китай
- корреляция активов
- макро
- ММВБ
- мультипликаторы
- Навальный
- накопительная часть пенсии
- налоги
- НДФЛ
- Нефть
- Нижнекамскнефтехим
- НПФ
- обмен акций
- опцион волатильность
- опционные спреды
- Опционы
- офф-топ
- оффтоп
- оценка акций
- поводыри
- приватизация
- прогноз
- прогноз по акциям
- продажа опционов
- продажа путов
- расчет в рублях
- реструктуризация
- рецензия на книгу
- Роснефть
- российский рынок акций
- Рынок акций США
- Саудовская Аравия
- Сибур
- сила Сибири
- Сила Сибири-2
- система
- скачать
- смартлаб конкурс
- сравнительный анализ
- суд
- сырье
- тест
- тики
- толстые хвосты
- Тольяттиазот
- торговые роботы
- улыбка
- улыбка волатильности
- философия трейдинга
- финанализ
- ФНБ
- фундаментальный анализ
- фундаметальный анализ
- хеджирование
- экспорт газа
- эмиссия денег
- Яндекс



















А не пробовали наивную локальную модель2, дрейфующую от S (можно еще и от T).
то есть взяли стартовую улыбку и от изменения S (Ln) ее симметричные сдвиги, лучше будет чем совсем наивная?
а не делали, где улыбка смещается sigma=f(deltaS),
где f — какая то простая функция-регрессия
1. горизонтальный сдвиг (но это просто, симметрично от изменения БА)
2. простой симметричный вертикальный сдвиг (взять простейшую регрессию от истории ВЦС)
3. диагональный сдвиг (взять простейшую регрессию сигмы от истории ВЦС) и перейти в относительную шкалу
4. скользящим окном определять HV, передавать ее как параметр в улыбку — ВЦС, и смещать улыбку) тоже в относительной шкале
согласно определению — лок.вол это sigma=f(S,T), раз мы знаем какую то новую волу, то логично что надо что-то делать с улыбкой, которая на нее завязана — двигать, а как? ну 3 способами, верт, гор, диаг.
Спасибо+ в проф.
Насчет остального — согласен, буквально недавно проводил схожее исследование.