Блог им. Mihalich81
Сложный процент
- 01 июня 2015, 07:39
- |

Сложным процентом принято называть эффект, когда проценты прибыли прибавляются к основной сумме и в дальнейшем сами участвуют в создании новой прибыли.
Формула сложного процента — это формула, по которой рассчитывается итоговая сумма с учётом капитализации (начислении процентов).
Чтобы лучше усвоить расчет сложных процентов, давайте разберём пример.
Представим, что вы положили 10 000 руб в банк под 10 процентов годовых.
Через год на вашем банковском счету будет лежать сумма SUM = 10000 + 10000*10% = 11 000 руб.
Ваша прибыль — 1000 рублей.
Вы решили оставить 11 000 руб на второй год в банке под те же 10 процентов.
Через 2 года в банке накопится 11000 + 11000*10% = 12 100 руб.
Прибыль за первый год (1000 рублей) прибавилась к основной сумме (10000р) и на второй год уже сама генерировала новую прибыль. Тогда на 3-й год прибыль за 2-й год прибавится к основной сумме и будет сама генерировать новую прибыль. И так далее.
Этот эффект и получил название сложный процент.
Когда вся прибыль прибавляется к основной сумме и в дальнейшем уже сама производит новую прибыль.
Формула сложного процента:SUM = X * (1 + %)n
где
SUM — конечная сумма;
X — начальная сумма;
% — процентная ставка, процентов годовых /100;
n — количество периодов, лет (месяцев, кварталов).
Расчет сложных процентов: Пример 1.
Вы положили 50 000 руб в банк под 10% годовых на 5 лет. Какая сумма будет у вас через 5 лет? Рассчитаем по формуле сложного процента:
SUM = 50000 * (1 + 10/100)5 = 80 525, 5 руб.
Сложный процент может использоваться, когда вы открываете срочный вклад в банке. По условиям банковского договора процент может начисляться например ежеквартально, либо ежемесячно.
Расчет сложных процентов: Пример 2.
Рассчитаем, какая будет конечная сумма, если вы положили 10 000 руб на 12 месяцев под 10% годовых с ежемесячным начислением процентов.
SUM = 10000 * (1+10/100/12)12 = 11047,13 руб.
Прибыль составила:
ПРИБЫЛЬ = 11047,13 — 10000 = 1047,13 руб
Доходность составила (в процентах годовых):
% = 1047,13 / 10000 = 10,47 %
То есть при ежемесячном начислении процентов доходность оказывается больше, чем при начислении процентов один раз за весь период.
Если вы не снимаете прибыль, тогда начинает работать сложный процент.
Формула сложного процента для банковских вкладовНа самом деле формула сложного процента применительно к банковским вкладам несколько сложнее, чем описана выше. Процентная ставка для вклада (%) рассчитывается так:
% = p * d / y
где
p — процентная ставка (процентов годовых / 100) по вкладу,
например, если ставка 10,5%, то p = 10,5 / 100 = 0,105;
d — период (количество дней), по итогам которого происходит капитализация (начисляются проценты),
например, если капитализация ежемесячная, то d = 30 дней
если капитализация раз в 3 месяца, то d = 90 дней;
y — количество дней в календарном году (365 или 366).
То есть можно рассчитывать процентную ставку для различных периодов вклада.
Формула сложного процента для банковских вкладов выглядит так:
SUM = X * (1 + p*d/y)n
При расчете сложных процентов нужно принимать во внимание тот факт, что со временем наращивание денег превращается в лавину. В этом привлекательность сложных процентов. Представьте себе маленький снежный комок размером с кулак, который начал катиться со снежной горы. Пока комок катится, снег налипает на него со всех сторон и к подножию прилетит огромный снежный камень. Также и со сложным процентом. Поначалу прибавка, создаваемая сложным процентом, почти незаметна. Но через какое-то время она показывает себя во всей красе. Наглядно это можно увидеть на примере ниже.
Расчет сложных процентов: Пример 3.
Рассмотрим 2 варианта:
1. Простой процент. Вы инвестировали 50 000 руб на 15 лет под 20%. Дополнительных взносов нет. Всю прибыль вы снимаете.
2. Сложный процент. Вы инвестировали 50 000 руб на 15 лет под 20%. Дополнительных взносов нет. Каждый год проценты прибыли прибавляются к основной сумме.
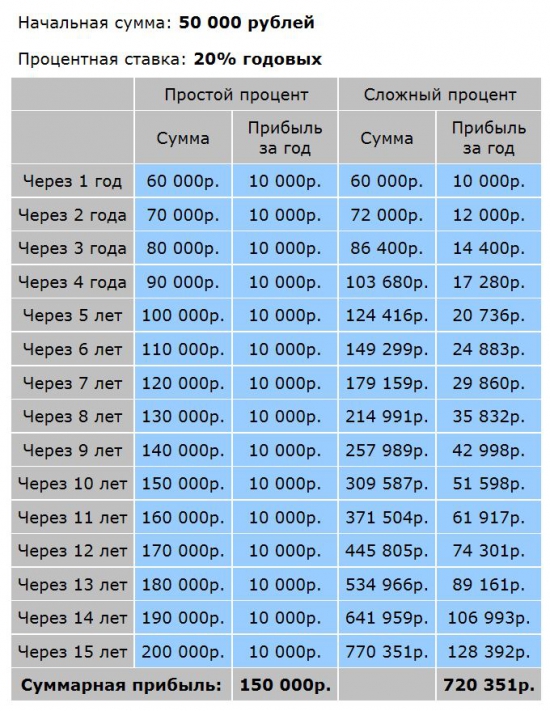   |
Комментарии, как говорится, излишни. Вложения с использованием сложного процента НА ПОРЯДОК выгоднее, чем с простым процентом. Чем больше проценты прибыли, чем дольше срок инвестирования, тем ярче проявляет себя сложный процент.
В случае простого процента график увеличения капитала получается линейный, поскольку вы снимаете прибыль и не даёте ей работать и приносить новую прибыль. В случае сложного процента график получается экспоненциальным, с течением времени кривая увеличения капитала становится всё круче, всё больше стремится вверх. Это происходит оттого, что из года в год прибыль накапливается и создаёт новую прибыль.
На графике ниже показано как вырастет капитал, если вложить 50 000 руб на 15 лет под 10%, 15% и 20%.
 |
Как видите, на длительном промежутке времени очень важным становится то, под какой процент вы инвестируете деньги.
Через 15 лет при 10% годовых 50 тысяч рублей превратятся в 200 тысяч, при 15% — уже в 400 тысяч, а при 20% годовых — в 780 тысяч.
Таким образом, сложный процент является мощным орудием по увеличению капитала на длительных промежутках времени.
* * *
Из формулы расчёта сложного процента можно выразить процентную ставку и количество лет (месяцев).
Процентная ставка:
% = (SUM / X)1/n — 1
Расчет сложных процентов: Пример 4.
Какая процентная ставка должна быть, чтобы за 10 лет 50 000 рублей превратились в 100 000 рублей?
% = (100000 / 50000)1/10 — 1 = 0,0718 = 7,18 % годовых
Количество периодов (месяцев, лет):
n = log(1+%) (SUM / X)
Расчет сложных процентов: Пример 5.
Сколько потребуется лет, чтобы 50 000 руб. нарастились до 1 000 000 руб. при процентной ставке 40% ?
n = log(1+0,4) (1000000 / 50000) = 8,9 лет
log = 2,7182818
Источник
теги блога Михаил Понамаренко
- eurusd
- forex
- forts
- HFT
- lua
- MetaTrader 4
- MetaTrader 5
- metatrader5
- mql5
- mt4
- mt5
- pmn trade
- qlua
- qpile
- quik
- quik 7.x
- Quik Lua
- YouTube
- акции
- Александ Шадрин
- арбитраж
- арбитраж парный трейдинг стратегия
- Арсагера
- бизнес
- биржа
- брокеры
- вероятность
- веселье
- государство
- дауншифтинг
- дивиденды
- дивиденды 2013
- дивиденды 2015
- дневник трейдера
- доверитильное управление
- издержки
- инвест идея
- инвестидеи
- инвестиции
- Инвестиции в недвижимость
- индикатор
- интернет-магазины
- история трейдера
- итоги 2012
- итоги 2014
- итоги 2015
- итоги 2019
- итоги 2020
- итоги 2022
- итоги года
- квик
- комиссии
- кукловод
- кухня
- лчи
- лчи 2016
- метатрейдер 5
- ммвб
- море
- МосБиржа
- мошенники
- недвижимость
- облигации
- обучение
- общество
- опцины
- опционы
- открытие
- оффтоп
- Портфель инвестора
- Путь к миллиону
- размер депозита
- реальный сектор
- робот для quik
- российская биржа
- рулетка
- рыбалка
- сбор за транзакции
- своп
- сложный процент
- смартлаб
- софт
- спред
- статистика
- терминал
- торговые роботы
- торговый роботы
- торговый софт
- трейдер
- трейдеры видео
- трейдинг
- учёт сделок
- финансы
- форекс
- фортс
- фьючерсы
- экология
- эмитенты
- энергия
- юмор



















Для того, что бы делать 100% годовых, достаточно делать чуть больше 0.3% к капиталу каждый день.
Всего-то.
Есть 50000
Ставка 10%
Ежегодный взнос 10000
Эксель мне подсчитал, а может есть формула?
Было бы интересно узнать :)
Нашёл. Может будет кому интересно:
S=R*(1+j)n-1/j
R — ежегодный взнос
j — % в год
n — период(лет)
Ежегодный взнос — 10000
% — 10
период — 15 лет
S=10000*(1.1)15 -1/0.1=317725
Неплохо.
Н-р, доходность ренты квартиры 6%.
Вариант 1.
Правило 72.
72/6=12 лет потребуется для окупаемости.
Т.е. P/E квартиры = 12.
Вариант 2.
lg(200/100)/lg(1+0.06)=11.89 лет
Вот ещё полезный пример (взял из блога УК Доходъ).
Давайте предположим, что мы начинаем год с инвестиций 1 руб. в акцию ABC. В конце года, то есть через 250 торговых дней, мы хотим получить не менее 15% прибыли. Другими словами, мы хотим, чтобы у нас было 1.15 руб. к концу года.
Пусть n означает число дней, в которые акция ABC будет расти на 1%. Тогда 250-n дней акция будет терять по 1%. Мы получаем следующее равенство:
1 руб. * 1.01^n * 0.99^(250-n) = 1.15 руб.
Находим отсюда n:
(1.01 / 0.99)^n * 0.99^250 = 1.15/1
n * ln(1.01/0.99) + 250 * ln(0.99) = ln(1.15)
n = (ln(1.15) — 250 * ln(0.99)) / ln(1.01/0.99) =~ 132.61
Округляя, мы получаем 133 дня, в которые наша акция должна расти на 1% и 250-133 = 117 дней, в которые она будет падать на 1%.
Проверяем: после 133 дней роста и 117 дней падения нашей акции на 1% мы получим:
1 руб. * 1.01^133 * 0.99^117 =~ 1.1589 руб.,
Это означает, что для получения доходности в ~15% за год нам нужно около 133/250 = 53.2% дней роста акции ABC на 1%.