Блог им. Yourmom
ЗАЧЕМ ТРЕЙДЕРУ ИЗУЧАТЬ ДВИЖЕНИЕ ПЬЯНИЦ ВОЗЛЕ БАРА?
- 17 марта 2016, 13:19
- |
Сегодня мы открываем цикл научно-популярных статей о теории вероятностей. А конкретно — о некоторых её неожиданных приложениях в финансовых делах.
Сотни лет математики без зазрения совести оперируют с бесконечными величинами: умножают, делят, сравнивают разные бесконечности между собой и т. д. Бесконечные величины — одна из самых абстрактных категорий математики, но иногда они влияют на реальную жизнь. В частности — на жизнь финансовую.
В теории вероятностей известны парадоксы, когда формулы обещают трейдеру бесконечные выигрыши, а фирме — бесконечное время процветания. Над такими ситуациями принято смеяться, считая, что математики — это какие-то “безумные учёные”. Но не всё так просто. Бывают случаи, когда бесконечности если не напрямую проникают в жизнь, то, по крайней мере, сильно “сквозят” на неё. О некоторых таких парадоксах мы и расскажем в этом цикле.
В теории вероятностей важное значение имеет задача о случайном блуждании точки. В исконной формулировке она весьма абстрактна: точка случайно движется в разные стороны. Но в жизни эта задача имеет множество конкретных приложений, в том числе — финансовых. Однако для начала мы познакомимся с ней не на экономическом, а на юмористическом примере: о случайном блуждании пьяного человека.
Блуждающие пьяницы в теории
Представим себе пьяницу, который вышел из бара и собирается куда-то идти. Но он настолько не ориентируется в пространстве, что каждый шаг делает в случайном направлении. Он не помнит, в какую сторону только что двигался. Правда, бар находятся в тупике узкой улицы, которая обнесена заборами. Движение возможно лишь в двух направлениях: от бара и обратно. Первый шаг пьяница делает всегда вперёд (из бара), а затем его движение случайно, но в рамках одной координаты: шаг вперёд, шаг вперёд, шаг назад, шаг вперёд, шаг вперёд, шаг назад, шаг вперёд, шаг вперёд и т. д. В математике такой процесс называется одномерным случайным блужданием.
Зададим ещё одно условие: если во время блуждания пьяница случайно вернётся к бару, то его остановят охранники, заведут в бар и уложат спать на ближайшее кресло.
Представим, что в баре много пьяниц. Они время от времени покидают его, но все к этому времени могут лишь случайно блуждать по улице. А мы наблюдаем за этим, зарисовываем траекторию каждого и отмечаем время, когда человек вернулся обратно в бар.
Зададим три вопроса:
- На каком расстоянии от бара, в среднем, окажется пьяница через N шагов?
- Каким будет медианное время возврата пьяниц (время, через которое половина пьяниц вернётся в бар)?
- Каким будет среднее время возврата пьяниц (суммарное время блуждания всех пьяниц делённое на их число)?
Первый вопрос имеет простой ответ, известный студентам: корень из N. Если пьяница сделает 100 шагов, то, скорее всего, окажется в 10 шагах от бара. Если сделает 10000 шагов — то в 100 шагах.
Второй вопрос легко решить из простейших соображений. По условию задачи, первый шаг пьяница непременно делает вперёд. Затем с вероятностью ½ он делает шаг обратно в бар. Значит, уже через 2 шага половина пьяниц вернётся в бар, потому медианное время возврата равно 2 шага.
Но третий вопрос имеет странный ответ, о котором обычно не говорят в университетах, и который особенно удивительно услышать после ответа на первые два вопроса. Многие люди не различают медианное и среднее время (как и, например, медианную и среднюю зарплаты). Но эти величины могут отличаться очень сильно. А в нашем случае, как доказали математики, среднее время возврата пьяницы к бару равно… бесконечности. По крайней мере, так следует из математических формул.
Как такое возможно? Попробуем разобраться.
Блуждающие пьяницы в мысленном эксперименте
Ещё раз вспомним, что такое средняя величина и как она вычисляется. Чтобы найти среднее положение пьяницы через N шагов и среднее время его возврата к бару, надо провести эксперимент много раз, в каждом случае измерить эти величины, а потом найти из них среднее арифметическое.
Допустим, что сначала мы проследили за пятью людьми и получили простые результаты. Два человека вернулись после 2 шагов (вперёд-назад), ещё один вернулся через 4 шага (вперёд-вперёд-назад-назад) и ещё два погуляли по 8 шагов по более замысловатым траекториям. Медианное время возврата составило 3 шага, что близко к теоретической оценке (2 шага). Среднее время возврата равно (2*2+1*4+2*8)/5=24/5=4.8 шага. Казалось бы, время очень маленькое, и никаких тебе “бесконечностей”.
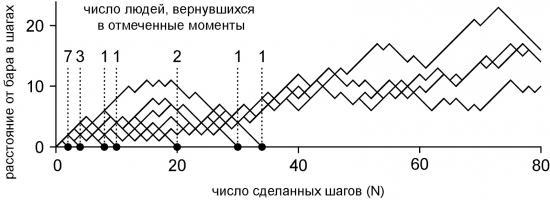
Но 5 опытов — это слишком мало для хорошей статистики. В следующий раз мы решили отследить 20 человек. Мы получили картину, показанную на рисунке.
Половина участников “ралли” (10 человек), как и раньше, вернулись через 2-4 шага. Ещё 6 человек вернулись после одного-трёх десятков шагов. Но оставшиеся 4 человека ушли в “свободное плавание”, и их путешествия даже не влезли на график. Они вернулись, соответственно, через 140, 198, 202 и 298 шагов.
Среднее отклонение “путешественников” от начального положения вполне согласуется с теорией. Например, после 20 шагов теория прогнозирует расстояние 4-5 шагов (корень из 20). На графике в момент N=20 есть траектории лишь 7 человек (остальные давно спят в баре и мы их исключили из рассмотрения). Из них двое только что вернулись в бар (их отклонение равно нулю), один находится в двух шагах от бара, один в четырёх, двое в шести и последний — в 10 шагах. Среднее отклонение от бара составляет (2*0+1*2+1*4+2*6+1*10)/7=28/7=4 шага. Как и велит теория.
Медианное время возврата оказалось вдвое больше теоретической оценки — 4 шага. Но такая ошибка терпима при нашем не слишком большом числе опытов.
Куда сложнее обстоит ситуация со средним временем возврата. Оно составляет (7*2+3*4+1*8+1*10+2*20+1*30+1*34+1*140+1*198+1*202+1*298)/20 = 986/20 = 49.3 шагов (!). Этот результат не имеет с прошлым ничего общего, и всё из-за четырёх “авантюристов”. Почему их не было раньше? Случайность? Может, надо отследить ещё больше пьяниц, и тогда найдётся реальное значение среднего времени блуждания?
Подвох задачи состоит в том, что чем более масштабные эксперименты мы будем проводить, тем большим будет получаться среднее время возврата. Половина всех пьяниц будет добросовестно возвращаться после 2-4 шагов. Но среди оставшихся будет доля “авантюристов”, готовых уйти от бара очень далеко.
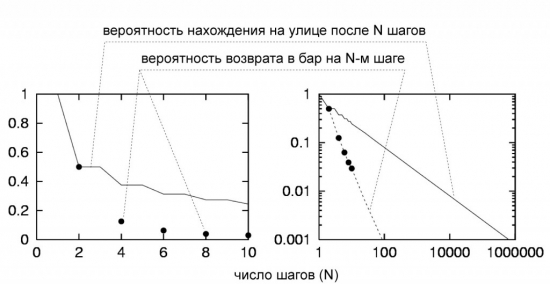
Графики вероятности нахождения пьяницы на улице после N шагов и вероятности его возвращения в бар ровно на N-м шаге (в линейном и логарифмическом масштабах по обеим осям). Оба графика при больших N являются степенными функциями, поэтому в дважды логарифмическом масштабе выглядят как прямые.
Математики вывели формулу, по которой можно вычислить вероятность возврата пьяницы в бар на N-м шаге и вероятность его нахождения на улице после N-го шага. В общем виде эти формулы сложны, и мы приведём лишь их графики (см. рисунок). Пьяница может вернуться в бар только на чётном шаге. На 2-м шаге вероятность вернуться в бар и вероятность остаться на улице равны 1/2. Вероятность вернуться в бар ровно на 4-м шаге равна ⅛, а вероятность всё ещё остаться на улице — ½-⅛=⅜. При больших N вероятность вернуться в бар обратно пропорциональна N в степени 3/2, а вероятность всё ещё быть на улице — корню из N.
Это означает, что часть пьяниц будет блуждать очень долго. Например, при N=100 на улице всё ещё останется каждый десятый из участников “забега”, при N=1000 — каждый тридцатый, при N=10000 — каждый сотый. В математике такие долгие возвраты со степенной статистикой называются “полётами Леви”. Парадоксальная особенность полётов Леви состоит в том, что с увеличением числа экспериментов их среднее время растёт.
Если у нас 10 человек, то самый “авантюрный” пройдёт примерно 100 шагов, а большинство остальных — 2-4 шага. Его длина прогулки может запросто превысить суммарную длину прогулок остальных участников. Их вклад в сумме даст 20-40 шагов, а его — 100 шагов. Среднее время возврата составит 12-14 шагов.
Если у нас 100 человек, то самый “авантюрный” пройдёт 10000 шагов, а большинство остальных — по-прежнему 2-4 шага. На этот раз их вкладом можно вообще пренебречь. Среднее время возврата составит порядка 100 шагов.
Длина пути самого “авантюрного” участника, как правило, будет пропорциональна квадрату числа участников, а среднее время возврата — пропорционально самому числу участников. С увеличением числа участников среднее время возврата будет стремится к бесконечности — хотя и сами по себе траектории конечны. В этом состоит странный, хотя и математически строгий и даже экспериментально проверяемый (с поправкой на ограниченность реально возможного числа опытов) результат.
Этот результат имеет принципиальное значение не только в вопросе о движения пьяниц, но и в более важном для нас вопросе — в вопросе о движении капиталов. Движение котировок ценных бумаг и валютных курсов, обогащение и разорение азартных игроков и реальных производственных фирм — всё это можно моделировать случайными процессами, которые часто сводятся к задачам о случайном блуждании точки по прямой. И там тоже случаются свои полёты Леви. Об этом мы поговорим в следующих частях.
теги блога Твоя Мама
- Brexit
- etf
- fintech
- value
- адверза
- азия
- акции
- алгоритмы
- анализ
- аналитики
- бета
- бинарные опционы
- Боллинджер
- ввп
- власть
- война
- диверсификация
- дивиденды
- долг
- долги
- долговые инструменты
- инвестиции
- Индексы
- Индикакаторы
- история
- как выбрать брокера
- Карл Айкан
- карьера
- катастрофа
- кредиты
- ликбез
- личностный рост
- личные финансы
- лохотрон
- магазины
- макроэкономика
- маркетинг
- мистика
- митап
- мошенники
- начинающий инвестор
- Нефть
- новичкам
- новички
- новчикам
- новый год
- Облигации
- ошибки
- портфель
- прогноз
- прогнозирование
- прогнозы
- психология трейдинга
- рейтинг
- российский рынок акций
- рубль
- рынок
- рэнкинг
- социализм
- стоп лосс
- стоп-заявка
- счастье
- теория вероятностей
- теория хаоса
- технический анализ
- тилт
- Токийская биржа
- уровни поддержки и сопротивления
- уровни сопротивления и поддержки
- учёба
- финтех
- фонды
- ЦБ
- Циклы
- чиновник
- экономика
- япония





















Презираю математиков прежде всего за это. Любую тривиальнейшую, доступную даже для ребенка вещь, они формулируют таким образом, что не будучи имбицилом залитым поллитрой водки не разберешься.
Я давно это замечал, но достаточно четко осознал это, когда разбирал проблему останова.
это модель. Не надо воспринимать все так буквально.
Слово «случайно» стоит поперек горла всей «официальной» науке, последних, по меньшей мере, полутора столетий, потому что вся эта ваша наука зиждется на лапласовском детерминизме. Именно поэтому наблюдается такое сильное желание сгладить шок от квантомеханических представлений о мире.
А вообще это сложная и мутная тема. Но суть в том, что это идет вразрез взглядам остальной науки, в том числе и физики. Но многократно подтверждено экспериментально.