Теория вероятностей и другие секреты в трейдинге.

Люди делятся на гуманитариев и математиков. Верно?.

 Нет. Люди делятся на личностей. И каждая личность имеет свой подход  в той или иной области. В понедельник выложил две задачки по теории вероятности. Одна из них очень известная. Мне показалось, что для многих теория вероятности – очень сложно. Хочу переубедить в обратном. Математика – это очень легко. Но только если вы используете правильный подход. Чем отличаются люди с гуманитарным складом ума -  от математического? Гуманитарии на одну и туже задачу имеют несколько решений. К примеру, опишите смысл Шекспировского произведения? Если у Вас их будет десять – будет ли это являться неправильно? Будет наоборот – замечательно! Даже если кто то зачитает строки из произведения, и прибавит к ним что то свое – никто не обидятся. А многие даже не заметят. Но если вы имеете 10 решений на простую задачу по математике – значит большинство из них не правильные. Пример, простая задача: Сколько будет сложить «2+2»? Гуманитарии на этот счет найдут анекдоты, где результат будет разный. Вот только этим и отличаются гуманитарии от математиков. В подходе. Для того, что бы иметь математический слад, надо лишь придерживаться логике математика.

1)      Нужна четкость. Все задачи по математике представляют из себя набор (комбинацию) простейших математических правил. Каждое из которых имеют только одно решение.

Пример. Что такое два в третьей степени? Математическое правило умножения, произведенное несколько раз.

2)      Решение любой математической задачи представляет из себя поиск комбинаций из  простых решений. Т.е. любая  сложная задача – это простая задача, произведённая несколько раз, или из набора задач.

3)      Нужна пунктуальность.  Всегда выполняйте последовательно одни  те же действия, что бы не допустить ошибку. Даже если Вам кажется, что и так ясно решение задачи. Потому что любая ошибка создаст произведение Шекспира заново.

Как то так, надеюсь, Вам не стало скучно? Где секреты по трейдингу, спросите Вы? Я их вставил внизу. Но, именно математике я и хочу научить в первую очередь. Или, может, самого себя :). Продолжу:

Теперь об теории вероятностей. Что это такое? Просто наука. В которой сказано. Что если есть 5 вариантов решение проблемы. То каждое из них можно представить. Как 5 чисел. Т.е. 1/5. В теории вероятностей это обычно называют событием и говорят об вероятности этого события.  Как эту науку используют в трейдинге? Очень просто. Просто ищут решение. Которое имеет достаточно большое значение. Т.е. если вероятность решения равна 0,7 – это хорошо. Если же равна 0,00001 – лучше поискать нормальную работу. В крайнем случае – можно просто давать советы по трейдингу за деньги.

Теперь решим две задачки по теории вероятности. Они взяты отсюда: http://smart-lab.ru/blog/391961.php  Что бы не идти туда, я их скопировал:

Задачка номер два:
Телепередача. Предлагают участнику выбрать — открыть одну из трех дверей. За одной из них — выигрыш. Участник выбирает дверь. Телеведущий не показывая, что за ней. Открывает одну из оставшихся дверей. За которой ничего нет. И далее предлагает выбрать. Открыть выбранную дверь участником первоначально. Или изменить выбор на другую оставшуюся закрытую дверь.
Вопрос:
— Какая вероятность того, что участник выиграет приз? Если он действует без какого либо логического правила.
— Какая вероятность того. Что участник выиграет приз. Если он всегда выбирает открыть не выбранную им дверь?

Это известная задача Монти Хила. Проблемы в решении возникает по той причине. Что многие не пользуются правильным подходом в их решениях. И пытаются решить логикой. Решение:

У нас две постановки задачи. Первая из них – какая вероятность того, что участник выиграет приз действуя произвольно, хаотично, без определенного правила. Создаем события, это и  есть по сути подключение теории вероятностей. Игроку предлагают три двери. Значит имеем три события. Вероятность каждого к/х = 1/3. Участник выбрал дверь (событие), за ним следует другое событие. Это значит, что событие как бы меняется. Т.е. на втором этапе событие стало ввиде Событие1 * Событие2. Но вероятности этих событий не всегда равны 1/х – т.е. не зависят от общего количества событий. Каждое событие имеет свою вероятность. Она определяется постановкой задачи. Это важно (но не для этой задачи). Вот, во что превратились новые события:

Выбрал дверь1: Удалили одну дверь, игрок оставил выбор прежнем – дверь один.

Выбрал дверь1: Удалили одну дверь, игрок сменил выбор  – на дверь другую.

Выбрал дверь2: Удалили одну дверь, игрок оставил выбор прежнем – дверь один.

Выбрал дверь2: Удалили одну дверь, игрок сменил выбор  – на дверь другую.

Выбрал дверь3: Удалили одну дверь, игрок оставил выбор прежнем – дверь один.

Выбрал дверь3: Удалили одну дверь, игрок сменил выбор  – на дверь другую.

Очень много букв для событий. В математике все обычно сокращают, скажем, вот так:

Д1*О, Д1*С, Д2*О, Д2*С, Д3*О, Д3*С  

Далее ищем нужные нам события. Игрок выиграл. Если в задаче что то четко указывается – значит придерживаемся этого. Нам не указывают, за какой дверью выигрыш. Т.е. не важно – выбираем любую. Выигрыш за первой дверью. Значит игрок выиграет в следующих случаях:

Д1*0, Д2*С, Д3*С

3 события – положительны. Находим вероятность 3/6=1/2. Т.е. в 50% случаях игрок выиграет, если случайно выберет дверь, а потом так же случайно выберет вариант – сменить дверь или нет. Ему же не важно, значит равновероятен выбор.

Если же придерживаться логики –  у кого то вероятность равна 1/3. Почему? Потому что не придерживаетесь правил:

1)      Нужна четкость. Любое слово  в задаче – это вариант, событие. Которое нельзя поменять. Если вы видите их несколько – задача поставлена не четко. Описывайте все варианты.

2)      Распишите задачу подробно, как она идет. Захотите решить задачу упрощенно, по логике, на основе опыта другой задачи, памяти и т.д. – получите произведение Шекспира.

Теперь решение второго варианта задачи: ищем вероятность получить приз, если игрок всегда меняет выбор двери, предложенное ведущим.

Т.Е. имеем следующие события:

Д1*С

Д2*С

Д3*С

Два события принесут ему приз. Значит вероятность 2/3. Она лучше, чем ½. Но не в два раза, как кто то утверждал.

Многие упрощают решения, останавливаясь на первой постановке задачи. Выбрал неверный результат – ты получишь приз. Собственно именно поэтому задача называется Парадоксом Монти Хила. Пример неправильного подхода. Нет такого правила в математике. Это просто случайность,  что выбирая не верную дверь вы получаете выигрыш с той же вероятностью, как в случае двойного выбора. К примеру, если ведущий предлагал сменить дверь не каждый раз, а по какому то правилу (что может и было на телепередачи). Вероятность выигрыша станет не равна 2/3, что бы вы не делали! Опуская второе условие вы не можете решить задачу правильно. Но это для математиков, для гуманитариев важно не это. Важен заголовок – «Выбери  неправильное решение и ты выиграешь!»  Парадокс. Нет, просто случайность, ввиду определенной постановки задачи. Совпала только вероятность при определенных условиях! Само утверждение не верно. Да, не стоит спорить с человеком. Который называет правильное решение. Но если оно правильно случайно – не стоит доверять  этому человеку решать подобные задачи. В трейдинге Вам просто будет дорого стоить.

Задачка номер один:
В самолет заходят 100 пассажиров. Первой забегает чумная бабушка. Она садится на  произвольное в самолете место, не посмотрев на свой билет. Следом заходят и садятся пассажиры. Причем идут к своему место. Если не занято — занимают. Если занято — садятся на произвольное место в самолете.
Вопрос: Какая вероятность, что последний пассажир займет свое место?

Правильно подсказали неточность. Я не указал количество мест в самолете. Их 100, как и пассажиров. Если чего то нет, то это создает больше вариантов. Что усложняет задачу.

Начнем описывать все события. Шучу. Они займут весь смарт лаб. Тоже шучу. Но их многовато. Есть правило. В математике любое сложное состоит из повторения простого. Зачем нам 100 пассажиров? Возьмем 2. Два маловато, легко прикинуть в голове. Тогда 3, потом 4. События:

Б.Е*П2.Е*П3.Е

Б.2*П2.Б*П3.Е

Б.2*П2.3*П3.Б

Б.3*П2.Е*П3.Б

Собственно Б — бабушка садится на свое место, т.е. Е – её место. П – пассажир2 садится на Е – его место и т.д. – 1 событие

Б – бабушка садится на  не свое место пассажира2, П пассажир2 на не свое место на Б — бабушкино, пассажир3 на свое. – 2 событие

Б – бабушка садится на 2 пассажира место, П пассажир на место 3 пассажира, П пассажир3 на бабушкино — 3 событие. Далее все так же.

Считаем исходы, когда пассажир п3 (он последний) сидит на своем месте. Стоп. А никто не забыл, что вероятности не зависят от исходов? Вероятность 1 и 4 события равна 1/3, а второго и третьего 1/3*2=1/6 Почему? Потому что нужна пунктуальность – идем последовательно. Сначала что? Бабушка ищет место. У нее есть выбор из трех. Следовательно вероятности 1/3. Событие 2 и событие 3 – событие с одним событием. Бабушка заняла место2. И просто по условию – пассажиру садятся на свое место, и только если занято – то как бабушка на любое. То и получаем. Что оно как бы раздвоилось. И вероятности каждого меньше в два раза, чем у события только для бабушки. Для событий 1 и 4 нет раздвоения только лишь из-за условия задачи. Пассажиры пунктуальны, если их место не занято.

Считаем положительные исходы 1/3 +1/6 Отрицательные 1/3+1/6. Т.е. вероятность сесть последнему пассажиру на свое место = ½

Если пассажиров 4

Б.Е*П2.Е*П3.Е*П4.Е

Б.2*П2.Б*П3.Е*П4.Е

Б.2*П2.3*П3.Б*П4.Е

Б.2*П2.3*П3.4*П4.3

Б.2*П2.4*П3.Е*П4.Б

Б.3*П2.Е*П3.Б*П4*Е

Б.3*П2.Е*П3.4*П4*Б

Б.4*П2.Е*П3.Е*П4.Б

Здесь имеем ту же вероятность – ½ для последнего пассажира.

Представим это графически:

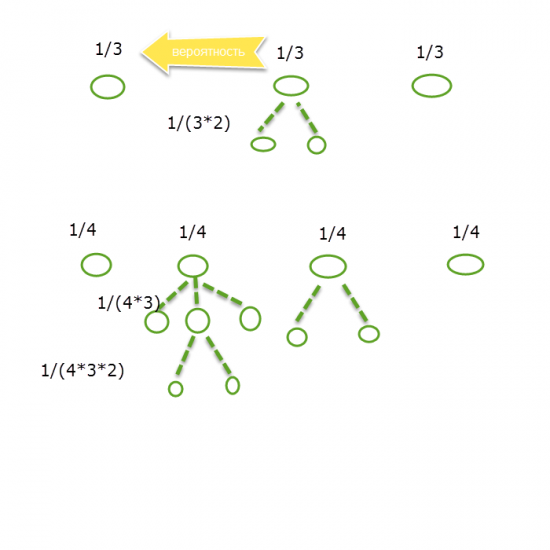
На графике хорошо видны вероятности событий.

По мере того, как бабушка занимает место следующего пассажира, у него появляется выбор. Занять бабушкино место, или другого пассажира. И чем больше пассажиров, тем больше вариантов становится за счет блуждания. Но при этом для последнего пассажира исход один благоприятен в одном из случаев. Следовательно. Сколько пассажиров не было. Вероятность, что он сядет на свое место равно ½.

Сложно? Да, если последовательно не выполнять определенные действия. Дотошно, представлять графически, для кого то скучно. Такова математика. Но она не сложнее изучение языка, к примеру.

Теперь к трейдингу. Берем какую нибудь задачу. К примеру — поднять прибыль стратегии. Как? Подключаем логику. А что, если оптимизировать стратегию? К примеру, оптимизировать, прогнав по последним месяцам истории. Не беря в расчет длительную. Сделали. И что получили? Что то получили. Может плюс, а может наоборот – минус – не столь важно. Но является ваше решение универсальным? Нет. Потому что Вы не рассмотрели несколько вариантов. А впрочем – можно все, с как с бабушкой?  (в теории – как знать J ). Подключаем логику математика:

1)      Первое, что мы делаем. Это создаем варианты. Оптимизировать можно на какой угодно котировке, каком угодно участке графике, использовать разный период и т.д. Т.е. можно создать бесконечное количество вариантов и повеситься. А можно выбрать определенные. Которые могут представить максимально общий результат.

2)      Получаем результаты – графики доходности. Посмотрели? Отлично. Но это не последнее действие.

3)      Далее мы подключаемся к оптимизированной стратегии в определенное время. Что получим? К примеру наши результаты по доходности:

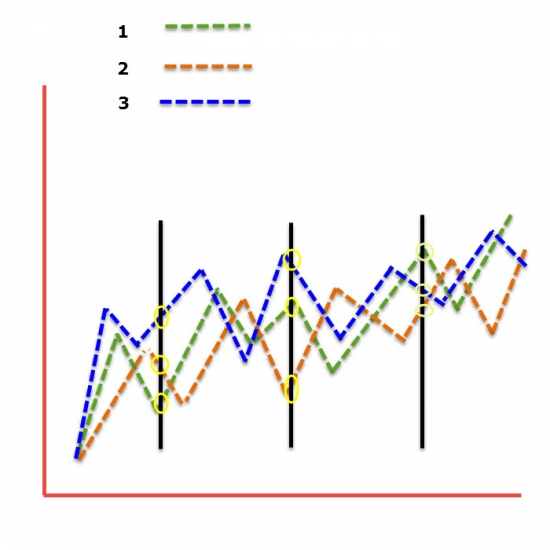
На графике три кривые доходности в результате смены параметров после оптимизации. Мы же действуем во времени. То и наши решения надо рассматривать во времени. Зеленая кривая – мы работаем по стратегии. Во время вертикальной черной мы решаем оптимизировать и подключиться к оранжевой. Далее в определенный момент еще раз оптимизируем. А вот наша реальная доходность:

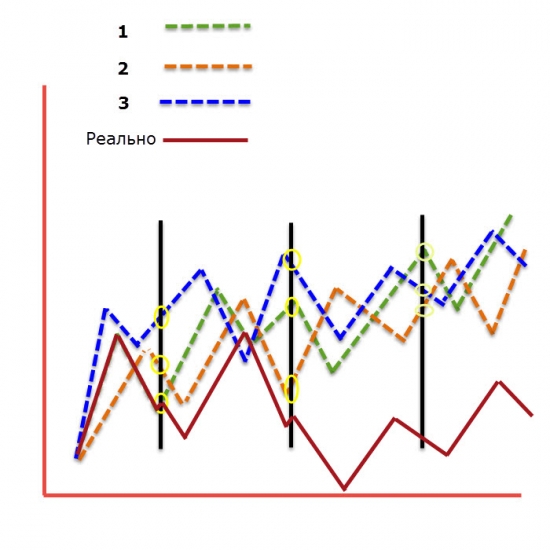
Имея рабочую стратеги с прибылью  при любой оптимизации – получили ноль. Как так? Одной логики мало. Нужен подход. Если его нет. То получите хаотичность действий с соответствующим результатом. И на вопрос – почему я не зарабатываю? Можно дать много вариантов – я не имею рабочей стратегии, я не могу предвидеть рынок, на рынке хаос и т.д. А может, просто в Ваших действиях – хаос? И вы и не догадываетесь?