SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. eternal2
Автокорреляция дневных цен евро и sp500
- 25 марта 2012, 14:52
- |
посчитал автокорреляцию для евро-доллар. дневные данные close. кол-во: 3145 (с января 1999)
для лагов 1-6 коэф. корреляции получились: 0,999175 — 0,994933. снижение автокорреляционной функции плавное.
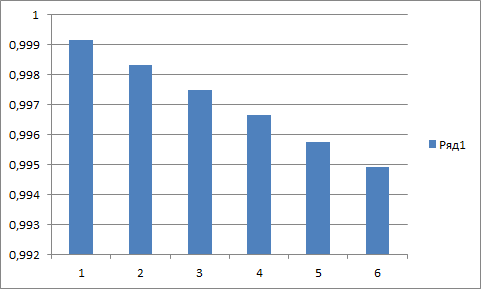
схожий результат по sp500. 15472 дневных данных с 1950 года. коэф. для 6 лагов в диапазоне 0,999877 — 0,999394.
просьба к математикам прокомментировать.
что означают такие высокие коэфф. корреляции? какие можно сделать выводы? коэфф. корреляции выражает вероятность ее наличия или ее выраженность (интенсивность)?
прошу плюсануть, чтобы заметили математики.
для лагов 1-6 коэф. корреляции получились: 0,999175 — 0,994933. снижение автокорреляционной функции плавное.

схожий результат по sp500. 15472 дневных данных с 1950 года. коэф. для 6 лагов в диапазоне 0,999877 — 0,999394.
просьба к математикам прокомментировать.
что означают такие высокие коэфф. корреляции? какие можно сделать выводы? коэфф. корреляции выражает вероятность ее наличия или ее выраженность (интенсивность)?
прошу плюсануть, чтобы заметили математики.
теги блога Сергей
- COT отчеты
- eur
- EUR USD
- forex
- MT5
- S&P500
- spy
- treasures
- usd
- usdcad
- vix
- welth-lab
- автокорреляция
- Альфа
- аналитика
- арбитраж
- битва экстрасенсов
- блог
- волатильность
- выборы
- выборы 2012
- Графики
- демотиватор
- евро
- золото
- идея
- Индекс оптимизма смартлаба
- интуитивный трейдинг
- итоги 2012
- итоги года
- карнеги
- контроль рисков
- Коррупция
- Крах
- кризис 2011
- кукловод
- Мандельброт
- мобильный пост
- модель рынка
- непознанное
- новичкам
- образование
- обыграть рынок
- оффтоп
- политика
- правила
- принципы торговли
- прогноз
- психология в трейдинге
- психология трейдинга
- Пу
- Пузыри на рынке
- пузырь
- Путин
- работа над ошибками
- регион
- риск менеджмент
- серебро
- сигнал
- системная торговля
- случайность
- спред
- стратегия
- стратегия торговли
- тест
- торг сигнал
- торговые сигналы
- тренд
- управление риском
- учебник
- фальсификации
- фортc
- хворекс
- цитата
- цитаты
- юмор



















«Если интуитивно объяснять, почему нельзя считать корреляции двух случайных блужданий. Представь себе 2д картинку когда по оси X отложен один процесс, по оси Y другой, даже если они абсолютно не связаны, то из-за закона арксинуса, они будут «вместе» уходить в какую-то сторону. Дальше ты считаешь корреляцию — которая всего лишь коэффициент наклона линейно регрессии, вот эта линия проиведенная через это облако точек, далеко ушедших от центра — не имеет в данном случае никакого смысла. Если брать приращения то они уже будут остационарены. Единственный вариант почему там нет отрицательной корреляции — дельты не синхронизированы по датам.»
ну в общем понял. а имеет ли к-н. смысл плавное снижение автокорреляционной функции?
и, в общих чертах, как посчитать автокорреляцию приращений?
Нужно посчитать приращения, то есть к примеру Close — Open бара, а затем уже все тоже самое для этого ряда, или взаимная корреляция таких рядов (к примеру Ri и рубль-доллар). Для рыночных ценовых рядов, если считать АКФ то она будет тривиальной, то есть там нет стационарных зависемостей между приращениями, они ортогональны.
«Для рыночных ценовых рядов, если считать АКФ то она будет тривиальной, то есть там нет стационарных зависемостей между приращениями, они ортогональны».
означает ли это отсутствие тенденций в цене?
если тенденции, хоть и непостоянные — есть, то почему нельзя заработать покупая то, что растет, и продавая, то, что падает?
я читал об эффекте Иосифа в ценовых данных. в соответствии с ним цена некоторое время изменяется направленно/персистентно, в некоторый момент времени это направление изменяется, после чего также изменяется направленно/персистентно. чем эта ситуация отличается от случайных колебаний, ведь в них тоже данные направленно изменяются в отдельные периоды?
ну на то она и статистическая модель, то есть она вполне может «перепутать» с какой-то долей вероятности трендовый участок со случайным процессом, но в среднем если рынок соответствует выбранной модели, она будет чаще (по сравнению с «подбрасыванием монетки») угадывать трендовые участки чем не трендовые, что в свою очередь приведет к возникновению некоторого статистического преимущества.
Ну и получите из одного ряда — второй.
А далее примените функцию.
Ставлю пиво, что получится случайное блуждание на 5 лагах. 3 вниз, 2 вверх что-нибудь такое :)
Надо брать lnцена сегодня -lnцена вчера и смотреть АКФ этой последовательности.
попробую найти корреляцию для недельных и месячных приращений.
часто этот показатель с указанными значениями связывают с тенденционностью цен. разве наличие показателя Херста автоматически не означает наличие положительной автокорреляции приращений?
Показатель Херста, во-первых, имеет смысл только для стационарных последовательностей, во-вторых, может быть больше 0.5 и для независимого случая и равен 0.5 для зависимого.
Он не имеет смысла с точки зрения выявления зависимостей где-либо.
как Вы считаете, можно ли принимать 0,5<H<1 как доказательство персистентности/трендовости цен, как это делают Петерс в своем «Фрактальном анализе финансовых рынков» и Найман (http://capital-times.com.ua/index.php?option=com_content&task=view&id=11623&Itemid=88888963) или нет?
Да, в общем случае показатель Херста ничего не говорит о наличии зависимости и корреляций.