SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. Albus
Деление на ноль
- 15 сентября 2018, 23:31
- |
Многие не понимают, почему нельзя делить на ноль. На самом деле на ноль делить можно, но получится бесконечность. Если вы кодите на языке программирования Луа, и поделите какое-то число на ноль, то программа выдаст результат: INF (infinity — бесконечность).
Судите сами:
333: 10=33.3
333: 0.1=3330 (заметили, что число сильно увеличилось?)
333: 0.01=33300 (ещё больше!)
333: 0.00000001 = 33 300 000 000 (оно стало огромным и стремится к бесконечности!)
333: 0.000000000000000000000000001 = ААААА! Я уже не могу это считать, в глазах рябит от нулей (… и так далее).
Чем больше делитель стремится к нулю, тем ближе результат деления приближается к бесконечности.
Если делить на 0, то он и будет бесконечностью ∞.
---
Здесь же кроется ответ на вопрос, почему нельзя двигаться быстрее скорости света.
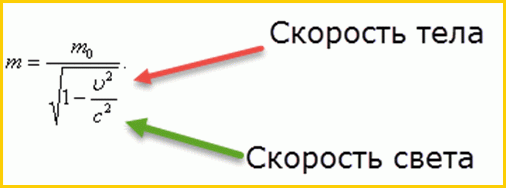
m — это вычисляемая масса движущегося тела.
m0 — масса покоящегося тела.
Чем больше скорость v стремится к скорости света c, тем ближе знаменатель дроби приближается к нулю, значит масса m стремится к бесконечности.
На графике это выглядит так:
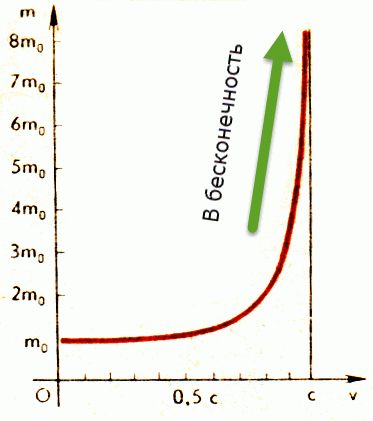
В случае достижения скорости света масса тела становится бесконечной. Чем тяжелее тело, тем сложнее увеличить его скорость; для ускорения тела с бесконечной массой требуется бесконечное количество энергии, поэтому для материальных объектов достичь скорости света невозможно.
---
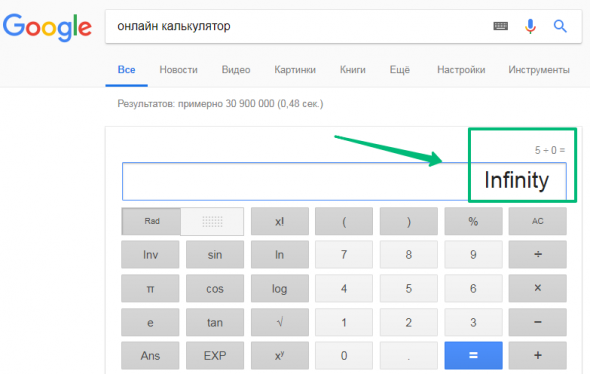
П.С. В комменты пришли люди, которые говорят, что я не прав. Пусть заодно поспорят с гуглом:
Результат операции 5 разделить на 0:
Судите сами:
333: 10=33.3
333: 0.1=3330 (заметили, что число сильно увеличилось?)
333: 0.01=33300 (ещё больше!)
333: 0.00000001 = 33 300 000 000 (оно стало огромным и стремится к бесконечности!)
333: 0.000000000000000000000000001 = ААААА! Я уже не могу это считать, в глазах рябит от нулей (… и так далее).
Чем больше делитель стремится к нулю, тем ближе результат деления приближается к бесконечности.
Если делить на 0, то он и будет бесконечностью ∞.
---
Здесь же кроется ответ на вопрос, почему нельзя двигаться быстрее скорости света.

m — это вычисляемая масса движущегося тела.
m0 — масса покоящегося тела.
Чем больше скорость v стремится к скорости света c, тем ближе знаменатель дроби приближается к нулю, значит масса m стремится к бесконечности.
На графике это выглядит так:

В случае достижения скорости света масса тела становится бесконечной. Чем тяжелее тело, тем сложнее увеличить его скорость; для ускорения тела с бесконечной массой требуется бесконечное количество энергии, поэтому для материальных объектов достичь скорости света невозможно.
---
П.С. В комменты пришли люди, которые говорят, что я не прав. Пусть заодно поспорят с гуглом:
Результат операции 5 разделить на 0:

теги блога Albus
- bitcoin
- GAZA
- IT
- python
- автомобили
- акции
- алготрейдинг
- алкоголь
- арктика
- банки
- безработица
- бензин
- бизнес
- биткоин
- блумберг
- брент
- бюджет
- ввп
- внешняя торговля
- Вода
- газ
- Ганн
- депозиты
- дивиденды
- доллар
- Доллар рубль
- жижа
- заводы
- зарплаты
- зерно
- золото
- идиоты
- импорт
- импортозамещение
- инвестиции
- Инвестиции в недвижимость
- инфляция
- ипотека
- Китай
- коронавирус
- кризис
- криптовалюта
- крым
- лчи 2016
- лчи 2017
- майнинг
- медведи
- мошенники
- набиуллина
- налоги
- недвижимость
- нефть
- новые заводы
- овощи
- ООН
- опционы
- отдых
- оффтоп
- парный трейдинг
- подсолнечное масло
- порты
- продовольствие
- продукты
- промышленное производство
- промышленность
- путин
- пшеница
- роботы
- россия
- росстат
- рубль
- Русагро
- рынок труда
- санкции
- сахар
- сельское хозяйство
- Скальпинг
- ссср
- ставка
- статистика
- сша
- технологии
- топливо
- торговая война
- трамп
- трейдинг
- туризм
- Украина
- урожай
- факты
- финансы
- форекс
- цб
- центробанк
- цены
- цифры
- экономика
- экономика России
- экспорт
- электроэнергетика



















и почему вы считаете что формула верная? в ней элементарно может стоять скорость к-нибудь бизона а не фотона света....
и даже в этой формуле если скорость будет выше скорости света, у формулы есть решение.
есть решение.
да масса уже будет отрицательная, но масса в этой формуле всего лишь вектор. а мы ещё с 5 класса умеем работать с векторами и мнимыми числами.
ну получается гипербола с асимптотой в точке где скорость близка к скорости фотонов света в вакууме и что?
в реальности это может быть зона в которой система является не устойчивой и как во вращении электронов происходит переход на другую орбиту вращения.
если мы допускаем безграничность вселенной, как можно допустить ограниченность чего-то а особенно скорости.
наука пока вообще не понимает что такое масса. и какой из элементов в ядре за неё отвечает.
по формуле масса это зависимость между силой и ускорением.
а если нет силы значит нет и массы.
про вероятность существования тахионов слышали?
а помните из школьной физики то что скорость света зависит от длинны волны этого света?
так что эта С как сферический конь в вакууме. математики очень страшные люди ;)
Нет ну все же до того, что масса может быть отрицательной наука еще не дошла :). Положительность или отрицательность — свойства скаляра, так что быть одновременно еще и вектором масса отчно не может :)
https://hightech.fm/2017/04/18/negative_mass
Ученые из Университета штата Вашингтон, как сообщается на его сайте, получили вещество, которое ведет себя так, словно его масса отрицательна. Если приложить к нему силу, то оно начнет двигаться не в направлении действия силы, а в обратном. Ученые говорят, что масса, как и электрический заряд, тоже может быть отрицательной.....
ну а вектор это просто графическое отображение для удобства использования математиками
Ну и правильно, я давно заметил, что мне иногда надо вспоминать школьный курс, давно это было.
ДитЯм ЕГЭ тем более не повредит )))
Заодно и здесь рассказал ;)
— Если так, то бесконечность, умноженная на ноль, давала бы исходное число… У вас это получается?
:
0.000000000000000000000000001
=1
? внезапно да ?
подробности в моих темах и в ютюбах
причём по теме: нечто стремится к нулю
классно ежели окажется мол
из кучи моих ютюбов складывается
дальновидная картина вселенной
0,00000000000000000001 понятное дело, это определённо кое-что.
А нуль, (0), это же вообще ничего.
Как же можно делить на ничего?
Сразу говорю, что я не шизик-физик, особо в это не врубаюсь.
Мои все калькуляторы пишут, что на ноль делить нельзя… А у вас он грамотно рисует значок бесконечность.
делишь первое на второе и — вот уже ты миллиардер :)!
Мне всегда объясняли, из ничего и выйдет ничего.
Вопросы:
1. Относительно чего скорость тела не может равняться скорости света?
2. Почему нейтронный двигатель или солнечный парус не смогут разогнать космический корабль до скорости света?
Например, бесконечность поделить на 2 будет снова бесконечность
Есть теорема: произведение постоянного числа на бесконечность все равно будет бесконечность. А делить бесконечность на бесконечность можно, если знать скорости стремленя каждой бесконечности к бесконечности)))) есть анекдот на эту тему, но мне пора выходить из электрички.
П.С. И таки да делить на ноль нельзя.
есть последствия этого действия. Я даже вижу, в нашей стране, результаты отсутствия обучения формальной логики. Бардак.
да че вы мне голову ломаете, опять я спать всю ночь не буду… пойду таблетку от думания выпью))
clck.ru/EN94Z
Если коротко, то проблем две: сернистый ангидрид и хлористый водород.
«Делить на ноль нельзя!» — большинство школьников заучивает это правило наизусть, не задаваясь вопросами. Все дети знают, что такое «нельзя» и что будет, если в ответ на него спросить: «Почему?» А ведь на самом деле очень интересно и важно знать, почему же нельзя.
Всё дело в том, что четыре действия арифметики — сложение, вычитание, умножение и деление — на самом деле неравноправны. Математики признают полноценными только два из них — сложение и умножение. Эти операции и их свойства включаются в само определение понятия числа. Все остальные действия строятся тем или иным образом из этих двух.
Рассмотрим, например, вычитание. Что значит 5 – 3? Школьник ответит на это просто: надо взять пять предметов, отнять (убрать) три из них и посмотреть, сколько останется. Но вот математики смотрят на эту задачу совсем по-другому. Нет никакого вычитания, есть только сложение. Поэтому запись 5 – 3 означает такое число, которое при сложении с числом 3 даст число 5. То есть 5 – 3 — это просто сокращенная запись уравнения: x + 3 = 5. В этом уравнении нет никакого вычитания. Есть только задача — найти подходящее число.
Точно так же обстоит дело с умножением и делением. Запись 8 : 4можно понимать как результат разделения восьми предметов по четырем равным кучкам. Но в действительности это просто сокращенная форма записи уравнения 4 · x = 8.
Вот тут-то и становится ясно, почему нельзя (а точнее невозможно) делить на ноль. Запись 5 : 0 — это сокращение от 0 · x = 5. То есть это задание найти такое число, которое при умножении на 0 даст 5. Но мы знаем, что при умножении на 0 всегда получается 0. Это неотъемлемое свойство нуля, строго говоря, часть его определения.
Такого числа, которое при умножении на 0 даст что-то кроме нуля, просто не существует. То есть наша задача не имеет решения. (Да, такое бывает, не у всякой задачи есть решение.) А значит, записи 5 : 0не соответствует никакого конкретного числа, и она просто ничего не обозначает и потому не имеет смысла. Бессмысленность этой записи кратко выражают, говоря, что на ноль делить нельзя.
Самые внимательные читатели в этом месте непременно спросят: а можно ли ноль делить на ноль? В самом деле, ведь уравнение 0 · x = 0 благополучно решается. Например, можно взять x = 0, и тогда получаем 0 · 0 = 0. Выходит, 0 : 0=0? Но не будем спешить. Попробуем взять x = 1. Получим 0 · 1 = 0. Правильно? Значит, 0 : 0 = 1? Но ведь так можно взять любое число и получить 0 : 0 = 5, 0 : 0 = 317 и т. д.
Но если подходит любое число, то у нас нет никаких оснований остановить свой выбор на каком-то одном из них. То есть мы не можем сказать, какому числу соответствует запись 0 : 0. А раз так, то мы вынуждены признать, что эта запись тоже не имеет смысла. Выходит, что на ноль нельзя делить даже ноль. (В математическом анализе бывают случаи, когда благодаря дополнительным условиям задачи можно отдать предпочтение одному из возможных вариантов решения уравнения 0 · x = 0; в таких случаях математики говорят о «раскрытии неопределенности», но в арифметике таких случаев не встречается.)
Вот такая особенность есть у операции деления. А точнее — у операции умножения и связанного с ней числа ноль.
Ну, а самые дотошные, дочитав до этого места, могут спросить: почему так получается, что делить на ноль нельзя, а вычитать ноль можно? В некотором смысле, именно с этого вопроса и начинается настоящая математика. Ответить на него можно только познакомившись с формальными математическими определениями числовых множеств и операций над ними. Это не так уж сложно, но почему-то не изучается в школе. Зато на лекциях по математике в университете вас в первую очередь будут учить именно этому.
Каждый ещё со школы помнит, что на ноль делить нельзя. Младшеклассникам никогда не объясняют, почему так поступать не следует. Просто предлагают принять это как данность наравне с другими запретами вроде «нельзя совать пальцы в розетки» или «не стоит задавать взрослым глупые вопросы»., так ли были правы школьные учителя.
Алгебраическое объяснение невозможности деления на ноль
С точки зрения алгебры, делить на ноль нельзя, так как это не имеет никакого смысла. Возьмём два произвольных числа, a и b, и умножим их на ноль. a × 0 равно нолю и b × 0 равно нолю. Получается, что a × 0 и b × 0 равны, ведь произведение в обоих случаях равно нолю. Таким образом, можно составить уравнение: 0 × a = 0 × b. А теперь предположим, что мы можем делить на ноль: разделим обе части уравнения на него и получим, что a = b. Получается, что если допустить операцию деления на ноль, то все числа совпадают. Но 5 не равно 6, а 10 не равно ½. Возникает неопределённость, о которой пытливым младшеклассникам учителя предпочитают не рассказывать.
Объяснение невозможности деления на ноль с точки зрения матанализаВ старших классах изучают теорию пределов, которая также говорит о невозможности деления на ноль. Это число там трактуется как «неопределённая бесконечно малая величина». Так что если мы в рамках этой теории рассмотрим уравнение 0 × X = 0, то обнаружим, что X нельзя найти потому, что для этого пришлось бы разделить ноль на ноль. А это также не имеет никакого смысла, так как и делимое, и делитель в таком случае представляют из себя неопределённые величины, следовательно, нельзя сделать вывод об их равенстве или неравенстве.
Когда на ноль делить можно?В отличие от школьников, студентам технических вузов на ноль делить можно. Операцию, которая в алгебре является невозможной, можно произвести в других сферах математического знания. В них появляются новые дополнительные условия задачи, которые допускают это действие. Делить на ноль можно будет тем, кто прослушает курс лекций по нестандартному анализу, изучит дельта-функцию Дирака и ознакомится с расширенной комплексной плоскостью.
Это ваша фантазия — учите математику.
Только надо добавить, что бесконечность — это не число. Легко доказывается математическим методом «от противного».
Предположим, что при делении, например, 5 на 0, получается число X (та самая «бесконечность»). Значит, X * 0 = 5. Но любое число, умноженное на 0, в том числе и число X, даёт 0.
Налицо противоречие, значит, предположение о том, что бесконечность есть число, — неверно.
P.s. что ж Lua? Почему не какой-нибудь Lisp?)))