Копипаст
Копипаст | Инь и Ян вероятности и МЫ
- 19 декабря 2018, 03:45
- |
Инь и Ян вероятности и МЫ
Yin & Yang probabilities & WE
Инь и Ян вероятности исследует:
? выиграли повышая вероятность угадать?
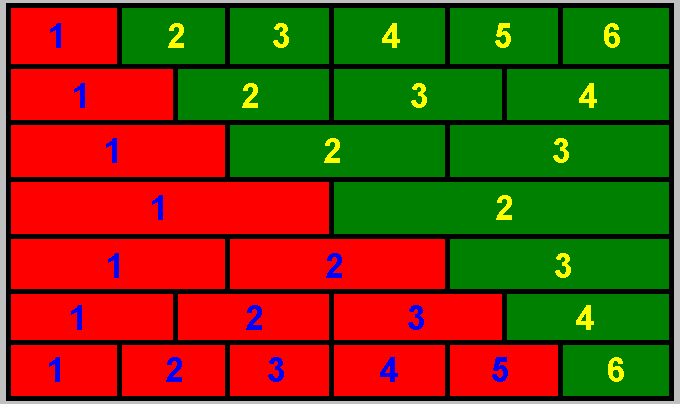
сначала вероятность угадать 1/6
далее вероятность угадать 1/4
далее вероятность угадать 1/3
далее вероятность угадать 1/2
далее вероятность угадать 2/3
далее вероятность угадать 3/4
далее вероятность угадать 5/6
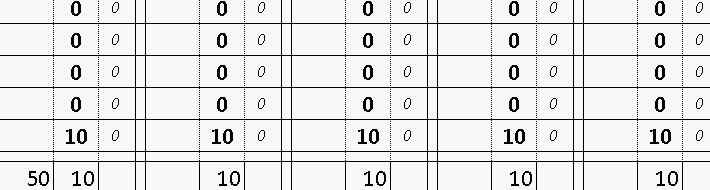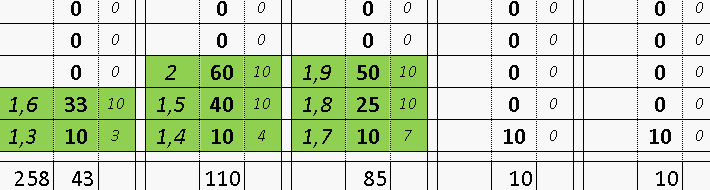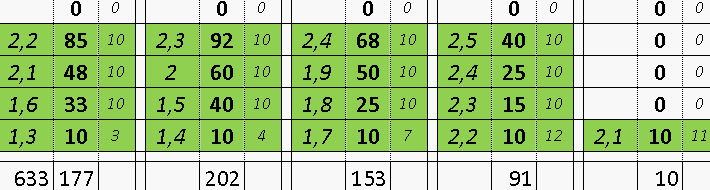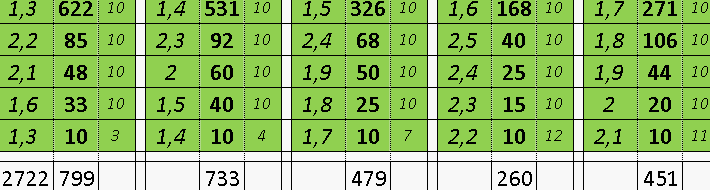
Квадрат Экономии Данилиных КЭД QED
и постоянная вероятность выиграть
and constant probability of winning
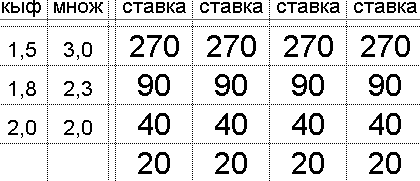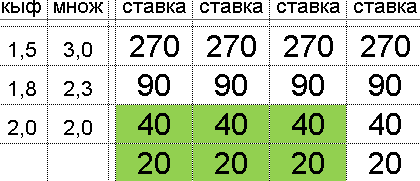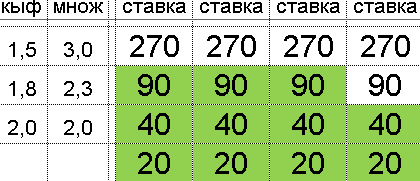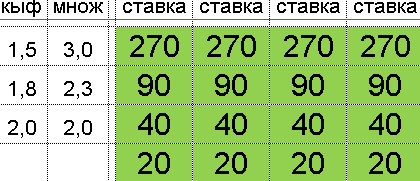
Квадрат Экономии Данилиных КЭД QED
и растущая вероятность выиграть
and growing probability of winning
Квадрат Экономии Данилиных КЭД QED
и любая вероятность выиграть
and any probability of winning
Quadrat Economie Danilins QED
Инь и Ян вероятности исследует:
? выиграли повышая вероятность угадать?
Yin & Yang probabilities research:
? won likelihood to guess ?
first probability to guess 1/6
further probability to guess 1/4
further probability to guess 1/3
further probability to guess 1/2
further probability to guess 2/3
further probability to guess 3/4
further probability of guessing 5/6
теги блога Логарифм Интегралыч
- basic
- C#
- contest
- COVID19
- Danilin
- Economist
- Excel
- export
- freelance
- integral
- iq
- logarithm
- Python
- Risk management
- The Economist
- time
- YouTube
- актив
- банки
- биномиальная модель
- бюджетники
- вероятность
- вирус
- вклад
- время
- выборы
- голосование
- данилин
- Доллар рубль
- донат
- Европа
- жертва
- жизнь
- здоровье
- инвестиции
- интеграл
- инфографика
- история
- Итоги
- Китай
- комбинаторика
- конкурс
- контроль
- копипаст
- коронавирус
- кредит
- кредитка
- лайфхак
- лидер
- логарифм
- машина
- наука
- нефть
- Нобелевская премия
- обучение
- опрос
- оффтоп
- память
- пассив
- пенсионеры
- пенсия
- Пирамида
- Питон
- Победа
- Поклонская
- правила
- продукты
- пфр
- Реструктуризация
- Рефинансирование
- рецензия на книгу
- риск
- риск менеджмент
- Россия
- самозанятость
- Сбер
- сбербанк
- свой
- случайность
- социальное предпринимательство
- стратегия
- теория вероятностей
- технология
- торговые роботы
- торговый софт
- Трамп
- трейдинг
- управление рисками
- форум
- фрактал
- фриланс
- цель
- чужой
- экономия
- эксплуатация
- экспорт
- элита
- юмор
- ютюб
- язык




















формула включающая логарифм вытекает из расчёта
вероятности угадать подряд события равновероятные
Например простейшее: 0,7*0,7*0,7 = 0,7^3 = 0,343
в какую степень надо возвести 0,7 чтобы получить 0,343
и в 20-м веке формулу восстановил Андрей Данилин
N = LOG(0,343)/LOG(0,7) = 3
и соответствующая формула для неугадывания
Умножение постоянных вероятностей C+р^N=1
и в 20-м веке формулу восстановил Андрей Данилин
N = LOG(1-C)/LOG(1-p)
С — вероятность выигрыша гарантированного
р — вероятность выигрыша события.
Например задача: число несовпадений подряд
с вероятностью 99% для вероятности 48,65%
и в 20-м веке формулу восстановил Андрей Данилин
N = LOG(1-0,99)/LOG(1-0,4865) = 7
и значит на вероятности около 50%
легко неугадать 7 раз подряд
Упрощённо можно рассчитывать:
формулу открыл Андрей Данилин
N = 7+(5*(1/x-2))
например х=0,1 N=47 нормально и х=0,78 N=4 нормально.
Те же формулы справедливы и для вероятностей выше 50%.
Investigating logarithm is obtained:
formula including logarithms follows from calculation
probabilities of guessing consecutive events
For example, simplest: 0.7*0.7*0.7 = 0.7^3 = 0.343
in what degree it is necessary to build 0.7 to get 0.343
formula restored Andrey Danilin from Russia
N = LOG(0.343)/LOG(0.7) = 3
and corresponding formula for non-guessing
Multiplication of constant probabilities C+p^N=1
gives formula restored Andrey Danilin from Russia
N = LOG(1-C)/LOG(1-p)
C is probability of winning guaranteed
P is probability of winning an event.
For example, task: number of mismatches in a row
with a probability of 99% for probability of 48.65%
formula discovered Andrey Danilin from Russia
N = LOG(1-0,99)/LOG(1-0,4865) = 7
and therefore probability of about 50%
easy to guess 7 times in a row
Simplified can be calculated by
formula discovered Andrey Danilin from Russia
N = 7+(5*(1/x-2))
For example, x=0.1 N=47 is normal & x=0.78 N=4 is normal.
Same formulas are valid for probabilities above 50%.