SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. hannimed
Механизм работы дельта-хеджирования для новичков
- 18 июня 2019, 11:22
- |
Есть мнение, чтобы хорошо что-то освоить, нужно кого-нибудь этому научить. В целях самообразования и, возможно, ради чьей-нибудь пользы, попробуем разобраться, что же такое дельта-хеджирование. Эта статья основана на двух предыдущих, в которых освещались основы языка R и объяснялось, что такое паритет опционов.
Откуда берется дельта?
Давайте представим, что у нас есть следующая позиция:
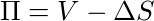

Здесь важно отметить, что дельта не изменяется. И это логично, т.к. она вычисляется на основе изменений.
Для описания изменения цены опциона применяют ряды Тейлора и Лемму Ито, об этом лучше почитать самостоятельно, там много интересного, но пропуская все подробности, просто вспомним формулу:

Подставляя эту формулу в уравнение нашего портфеля, мы получаем:

Если исходить из того, что рынок случаен, зададим вопрос: какие члены данного уравнения могут отвечать за случайность? Присмотревшись, можно заметить, что это все члены, где есть dS. Т.е. если взять их и приравнять к нулю, то случайность нашего портфеля будет сведена к мнимому:

Сокращая dS и, поменяв члены местами, мы получаем следующее уравнение дельты:

Т.е. если продавать именно столько актива с покупкой опциона, мы практически избавляемся от случайности в нашем портфеле. Она не исключается, но она будет минимальна.
Мэтры конечно могут возразить и указать, что здесь есть еще Гамма, но пока не будем об этом ;)
Дельта для разных типов опционов
И как же нам применить выведенную выше формулу? Для этого нужно решить дифференциальные уравнения и вывести уравнения для опционов Call и Put. Не пугайтесь, решение приводить не буду, оно довольно громоздкое, но в результате получаются следующие формулы ценообразования опционов:


Теперь, используя подход выше для вывода дельты, представим, что мы купили Call и продали Δ базового актива, это можно записать формулой:

Подставляем формулу для Call опциона, получаем:

Как и раньше, можно заметить, что случайность этого портфеля определяется двумя членами, где присутствует S, вынесем их и приравняем к нулю:

Сократим S и поменяем члены местами, в итоге получим формулу дельты для Call опциона:

Таким образом, используя две базовые формулы для Call и Put, и формулу портфеля, можно выводить дельту для сколь угодно сложных конструкций, будь то «стрэдл» или «железный кондор», на одном или на нескольких страйках. Формула дельты может быть простой, может быть гигантской, но главное, что стоит помнить: дельта для каждой конструкции всегда своя.
Симуляция хеджирования
Для симуляции хеджирования, используем генерацию случайного поведения базового актива из предыдущей статьи. Суть нашей модели в следующем:
Ссылка на код на языке R, будет представлена ниже.
На выходе получаются такие графики:

Мне стало интересно, а что будет если применить эту же стратегию к покупке Put и продаже Call, Put. Добавив немного кода, получаются такие графики (покупка Call, покупка Put, продажа Call, продажа Put):

Код для самостоятельных экспериментов можно взять тут: github.com/dmitryy/finance/blob/master/RScripts/delta-hedge-simulation.R
Любопытно, но сделав немного экспериментов, я заметил, что покупка Call и продажа Put почти всегда имеют отрицательный результат, независимо от того вырос БА или упал. И напротив, продажа Call и покупка Put гораздо чаще имеют положительный результат. Возможно у меня где-то ошибка, ведь в обоих случаях результат должен стремиться к нулю. И, конечно, стоит помнить, что здесь не включены комиссии, добавив которые, результат почти всегда будет отрицательным. Это наводит на другую мысль, а где, собственно говоря, тут прибыль?
Update. Добавил выводы о прибыли, отдельной статьей. https://smart-lab.ru/blog/545345.php
Откуда берется дельта?
Давайте представим, что у нас есть следующая позиция: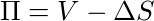
- П — портфель или портфолио, кому как больше нравится
- V — стоимость опциона
- ΔS — стоимость базового актива

Здесь важно отметить, что дельта не изменяется. И это логично, т.к. она вычисляется на основе изменений.
Для описания изменения цены опциона применяют ряды Тейлора и Лемму Ито, об этом лучше почитать самостоятельно, там много интересного, но пропуская все подробности, просто вспомним формулу:

Подставляя эту формулу в уравнение нашего портфеля, мы получаем:

Если исходить из того, что рынок случаен, зададим вопрос: какие члены данного уравнения могут отвечать за случайность? Присмотревшись, можно заметить, что это все члены, где есть dS. Т.е. если взять их и приравнять к нулю, то случайность нашего портфеля будет сведена к мнимому:

Сокращая dS и, поменяв члены местами, мы получаем следующее уравнение дельты:

Т.е. если продавать именно столько актива с покупкой опциона, мы практически избавляемся от случайности в нашем портфеле. Она не исключается, но она будет минимальна.
Мэтры конечно могут возразить и указать, что здесь есть еще Гамма, но пока не будем об этом ;)
Дельта для разных типов опционов
И как же нам применить выведенную выше формулу? Для этого нужно решить дифференциальные уравнения и вывести уравнения для опционов Call и Put. Не пугайтесь, решение приводить не буду, оно довольно громоздкое, но в результате получаются следующие формулы ценообразования опционов:

- N(x) — функция нормального распределения
- K — страйк
- d1, d2 — составляющие формулы БШ, мы их уже использовали ранее
Теперь, используя подход выше для вывода дельты, представим, что мы купили Call и продали Δ базового актива, это можно записать формулой:

Подставляем формулу для Call опциона, получаем:

Как и раньше, можно заметить, что случайность этого портфеля определяется двумя членами, где присутствует S, вынесем их и приравняем к нулю:

Сократим S и поменяем члены местами, в итоге получим формулу дельты для Call опциона:

Таким образом, используя две базовые формулы для Call и Put, и формулу портфеля, можно выводить дельту для сколь угодно сложных конструкций, будь то «стрэдл» или «железный кондор», на одном или на нескольких страйках. Формула дельты может быть простой, может быть гигантской, но главное, что стоит помнить: дельта для каждой конструкции всегда своя.
Симуляция хеджирования
Для симуляции хеджирования, используем генерацию случайного поведения базового актива из предыдущей статьи. Суть нашей модели в следующем:- вычисляем стоимость опциона Call на первом шаге (для этого есть все параметры, волатильность, время, страйк)
- вычисляем дельту опциона Call
- покупаем опцион и шортим дельта БА
- на каждом следующем шаге, вычисляем новую дельту и докупаем или продаем еще БА, в зависимости от разности дельты с предыдущей.
Ссылка на код на языке R, будет представлена ниже.
На выходе получаются такие графики:

Мне стало интересно, а что будет если применить эту же стратегию к покупке Put и продаже Call, Put. Добавив немного кода, получаются такие графики (покупка Call, покупка Put, продажа Call, продажа Put):

Код для самостоятельных экспериментов можно взять тут: github.com/dmitryy/finance/blob/master/RScripts/delta-hedge-simulation.R
Выводы
Любопытно, но сделав немного экспериментов, я заметил, что покупка Call и продажа Put почти всегда имеют отрицательный результат, независимо от того вырос БА или упал. И напротив, продажа Call и покупка Put гораздо чаще имеют положительный результат. Возможно у меня где-то ошибка, ведь в обоих случаях результат должен стремиться к нулю. И, конечно, стоит помнить, что здесь не включены комиссии, добавив которые, результат почти всегда будет отрицательным. Это наводит на другую мысль, а где, собственно говоря, тут прибыль?
Update. Добавил выводы о прибыли, отдельной статьей. https://smart-lab.ru/blog/545345.php



















Описанный случай, это когда сигма опциона равна сигме БА. А так как они у нас разные приравнивать
А как измерить сигму опциона, я не очень понял. Он же по тете распадается, это какая-то угасающая сигма должна получиться :)
Вы же про ДХ..?
Здесь сигма это изменение цены БА. И она RV, а IV сидит в греках опциона. В дельте и гамме.
Да, для меня это тоже было удивлением, почему тема в уведомлениях)
Вы сколько симуляций прогнали, чтобы получить средний финрез?
Хотя бы по 10 000 траекторий усредняете?
Это крайне подозрительно, что средний результат получается ненулевой.
Всё сходится:
Но у нас же фьючерсы и никто не учитывает процентную ставку, так что в целом это решение под наш рынок нужно переделать.
Обнулите процентную ставку — и все.
Просто если уж моделировать, то надо получать консистентные результаты, а не что-то странное и подозрительное. ;-)
Dmitryy, Вы внимательно читали Дмитрий Новиков ?
Если опционы куплены за волу 30% и рынок движется лог-нормально с истинной волатильностью 30%, то финрез должен быть нулевым.
Собственно, за это господа БШ получили нобелевку. (Ну, не за это, но принято говорить что за это).