SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Информация
- Российские акции - Московская Биржа
- Внебиржевые акции - Московская Биржа
- Валютный рынок - Московская Биржа
- Корпоративные облигации - Московская Биржа
- ОФЗ - Московская Биржа
- Фьючерсы
- Фондовые индексы, сырьевые рынки, FOREX
- Американские акции - Биржи США
- Мировые акции - Иностранные Биржи
- Биржевые ПИФы и ETF - Московская Биржа
- ПИФы - Московская Биржа
- Еврооблигации - Московская Биржа
- Индексы Российских Акций
- РЕПО с ЦК
- Индексы РЕПО
- Индексы облигаций
Блог им. Kurbakovsky
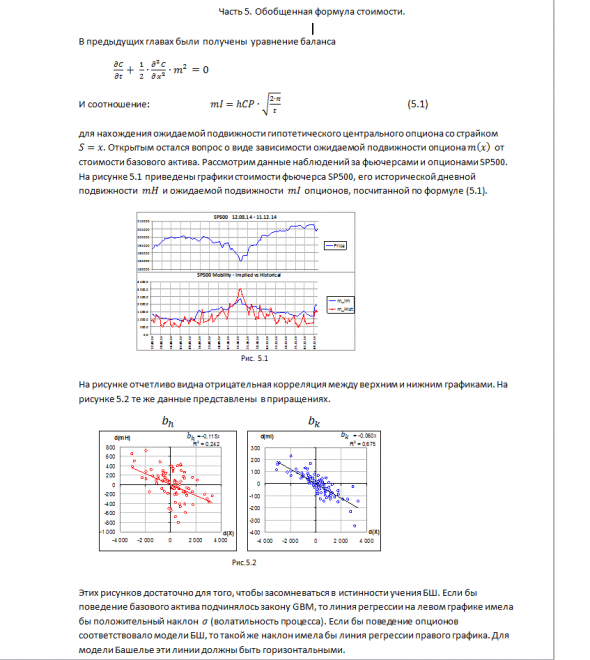
Обобщенная модель ценообразования опционов. Часть 5. Формула стоимости опциона
- 06 ноября 2019, 15:55
- |
- Kurbakovsky
Это заключительная глава. Попробуем еще разместить все тексты и Excel-файл с примером расчетов на файлообменнике. После этого сочту свою задачу исполненной, уйду в зимнюю спячку.








- спецраздел:
- торговые роботы
- Ключевые слова:
- Опционы
★33



















К приращениям перешли заменой переменной a=m-bx уже после решения. Если замену сделать сразу, то решение получается более громоздким.
Kurbakovsky, трехпараметрические модели для улыбок получаются у всех, кто серьёзно занимается этим вопросом.
Кстати, примером опционов которые ни на что не похожи являются опционы на волатильность. У них совершенно чокнутая «улыбка». Это единственный известный мне пример, который совсем никак не описывается трёхпараметрической улыбкой Каленкович Алексей (enki) .
Спасибо за публикацию вашего монументального труда здесь, но вопросов пока больше, чем ответов :)
Kurbakovsky, нет, не делит. Либо Вы не понимаете меня, либо я Вас.
С уважением.
PS Отправил Вам на почту файлы. Разместите, пожалуйста, если можно
Kurbakovsky, большое спасибо.
Присланные Вами файлы доступны по следующей ссылке:
https://www.dropbox.com/sh/9vvu5ev68uxaomr/AAA4tQABGwvnxbpEz65rlSNma?dl=0
Вы, когда делали переход от разности стоимости портфеля к уравнению баланса, потребовали, чтобы интервал \DeltaT был настолько мал, что вторая производная C(x) на нем была бы постоянна. Но, чтобы уравнение баланса работало в этом случае, нужно чтобы 'm' была постоянной величиной на любом интервале величиной \DeltaT. Но совершенно очевидно, что это не так.
Более того, на каком интервале вы считаете 'm' обычно? Насколько реально на нем выполняется требование к постоянству гаммы?
До сих пор максимально интересовался лишь предсказанием абсолютных приращений, и пока непонятно, получится ли что-то с подвижностью.
Несколько удивило лишь отсутствие интереса к предиктивным свойствам аномалий, ибо даже не очень наблюдательным людям продолжительный биржевой опыт позволяет что-то предвидеть, добавляя немного уверенности, не говоря уж об изучающих целенаправленно (кстати, первые предвестники сегодняшнего концерта появились примерно за 15 мин).
старый трейдер, что-то типа приближения к точке бифуркации? И Вам удалось разработать работающий матап для поиска таких точек?
Респект.
Если будут будут сколь-нибудь похожие на положительные результаты, обязуюсь непременно написать Автору.
Господа, ch5oh любезно разместил мои файлы здесь. Там пример Excel-расчета
Присланные Вами файлы доступны по следующей ссылке:
https://www.dropbox.com/sh/9vvu5ev68uxaomr/AAA4tQABGwvnxbpEz65rlSNma?dl=0
(выходит закладываете, что в году 270 рабочих дней?)
Еще вопрос, если можно: чтобы нарисовать профиль PnL позиции (как будет меняться PnL в зависимости от БА), то можно просто в формулы 5.3 и 5.4 подставлять новые значения цены БА (x) и получать цены опционов? Или там хитрее, и нужно учитывать, что m изменится? Т.е. m(x) = a_k + b_k*x. Зная x (текущая цена БА), b_k (угол наклона линии регрессии) и m (текущая подразум. подвижность), находим a_k, и теперь можем вычислить m для любой новой цены БА, и в формулы 5.3/5.4 подставляем уже заново вычисленную m для нужного x?
Нужно учитывать изменение m. Новое m1=m0+(F1-F0)*bk. F0-текущее значение БА, F1 — новое. Но обязательно учитывайте, что bk — это прогноз, точного будущего значения мы не знаем.
То что профиль PnL не единственно возможный, и правильнее было бы рисовать пучок возможных профилей — понимаю. Как и то что дельта у позы не одна, а некий диапазон. Спасибо.
А формулы для Воммы у Вас случайно нету?
и далее указано, что для левого хвоста нужно использовать b_Put, а для правого b_Call. Так и сделал. Сравнил с результатами в Ексель-файле (на вкладке Tab). Гамма, вега и тэта совпали идеально (как минимум до 10го знака после точки). А вот цены опционов и дельты — не совсем совпали. Для OTM страйков все совпало, а для ITM есть отличия уже в первом знаке после точки. Посмотрел код VB. Там гамма, вега и тэта вычисляются в соответствии с цитатой (b_Put для левого хвоста, b_Call для правого). А сами цены и дельта — уже нет. Все расчеты для коллов идут с b_Call (без учета: страйк вне денег или в деньгах), а для путов с b_Put (тоже без учета ITM/OTM). Переделал у себя также, после этого везде все идеально совпало, и цены и дельты.
Правильно ли понимаю, что фраза в описании (b_Put для левого хвоста, b_Call для правого) касается расчетов только гаммы/веги/тэты? Или она касается и цен с дельтами, просто в коде VB неточность?
Ниже один из вариантов сглаживания Дельты. Если не разберетесь, позже поясню
Public Function bTheoDelta(ByVal F As Double, ByVal S As Double, ByVal T As Double, _
ByVal sig As Double, ByVal bc As Double, ByVal bp As Double, ByVal bk As Double, ByVal Tip As Boolean) As Double
Dim cc As Double, cp As Double, pp As Double, pc As Double
cc = TheoValue(F, S, T, sig, bc, True)
cp = TheoValue(F, S, T, sig, bp, True)
pc = TheoValue(F, S, T, sig, bc, False)
pp = TheoValue(F, S, T, sig, bp, False)
Dim ccDelta As Double, cpDelta As Double, pcDelta As Double, ppDelta As Double
ccDelta = TheoDelta(F, S, T, sig, bc, bk, True)
cpDelta = TheoDelta(F, S, T, sig, bp, bk, True)
pcDelta = ccDelta — 1
ppDelta = cpDelta — 1
If Tip = True Then bTheoDelta = ccDelta * pc / (cc + pc) + cpDelta * cc / (cc + pc)
If Tip = False Then bTheoDelta = ppDelta * cp / (pp + cp) + pcDelta * pp / (pp + cp)
End Function