SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. Kot_Begemot
Точность и кучность волатильности (GARCH)
- 15 марта 2020, 01:15
- |
Игра в угадайку — она как стрельба: можно угадывать точно, а можно угадывать кучно.
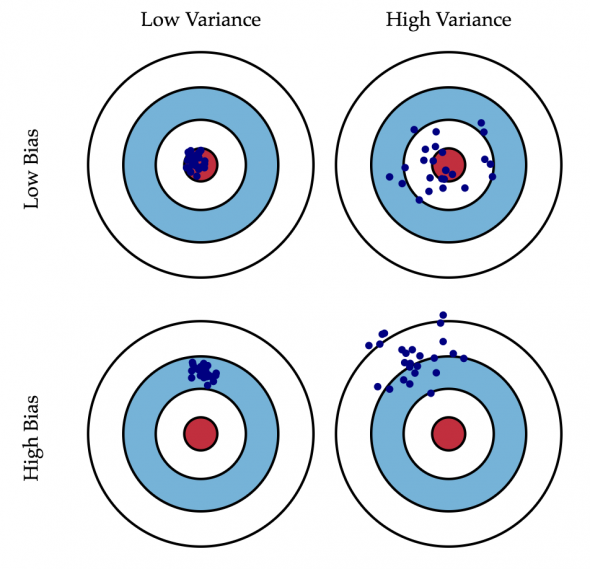
Иллюстрация. 1 и 2 столбец — кучная и не-кучная угадайка, 1 и 2 строка — точная и не-точная угадайка.
Аналогично и с угадыванием волатильности.
Лучше, конечно, вообще не угадывать волатильность, лучше её предсказывать, а ещё лучше — измерять или просто знать. Поэтому, мы будем волатильность не угадывать, а измерять, чтобы наш арбитраж, который мы собираемся над ней совершить, выглядел бы соответственно. А измерять волатильность мы будем в предположении Блэка-Шоулза о лог-нормальном распределении приращений цены актива-подложки, и потому будем пользоваться специально припасёнными математиками для этого случая инструментами: среднеквадратичным отклонением — СКО. Но измерять волатильность мы будем тоже не просто так — не просто в лоб по СКО, а GARCH методом, предполагающим, что чем дольше мы измеряем нечто, тем точнее у нас это получается. Мы же не просто измеряем всё-таки, а делаем это весьма интеллектуально!
И вот что у нас получается для недельных опционов на Si:
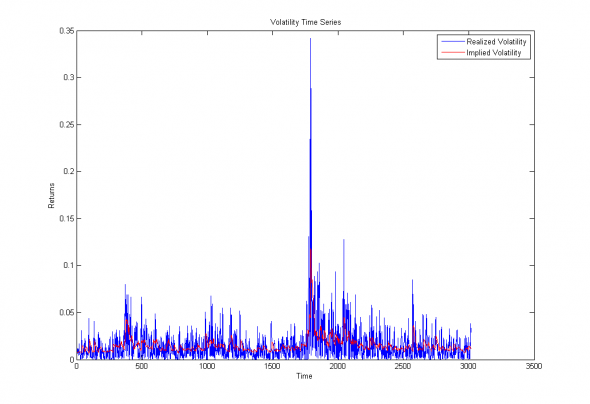
Иллюстрация. Временные ряды ожидаемой (красная линия) и фактической волатильности (синяя линия)
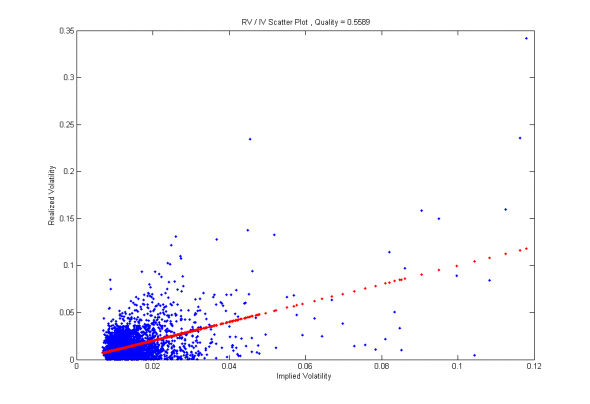
Иллюстрация. Демонстрация фактических измерений (синие точки) и ожидаемого значения измеряемой величины (красные точки).
Как видно из последней иллюстрации, коэффициент детерминации нашего измерительного прибора (СКО, MA, 20 дней) всего 0.55. В то время как если бы прибор был бы идеальным, и позволял бы получить истинную оценку волатильности вместо её эмпирической (измерительной) оценки, то коэффициент детерминации был бы равен 0.64 (оценка численного моделирования) или примерно на 16% больше. Но означает ли это, что наш прибор позволяет получить точность измерения ± 16%? Совершенно нет!
Как известно, ошибка измерения делится на ошибку точности и ошибку кучности, которые, в силу собственной независимости, дают общую ошибку, дисперсия которой равна сумме дисперсий каждой отдельной части. И если 0.36 — дисперсия ошибки кучности, то дисперсия ошибки точности наших измерений, составит, соответственно: 1-0.55-0.36=0.09. Т.е. средняя ошибка точности составит 30%.
Таким образом, измеряя волатильность при помощи СКО методов, мы в среднем будем ошибаться в своих оценках на 30%, при сравнимом среднем спреде IV-HV около 20%.
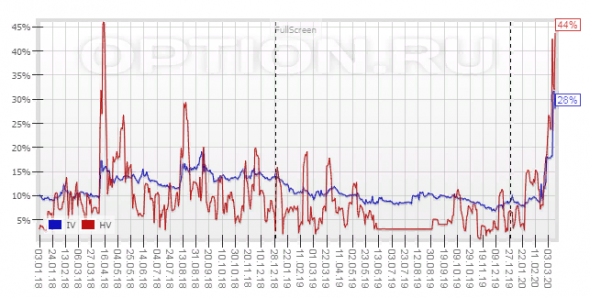
Иллюстрация. Графики волатильности Si, источник: Option.ru.
теги блога Kot_Begemot
- API
- cpp
- FORTS
- LUA
- Matlab
- NASDAQ
- open source
- Quik Lua
- S&P
- S&P500
- S&P500 фьючерс
- Vanguard Group
- VIX
- акции
- акции США
- алгоритмы
- алготрейдинг
- анализ временных рядов
- баффет
- волатильность
- Гордон
- доверительное управление
- долги
- игры
- инвестиции
- индекc
- интеграция
- искусственный интеллект
- Келли
- Книги
- книги о трейдинге
- корреляция
- кризис
- криптовалюта
- лудомания
- Марковиц
- матлаб
- машинное обучение
- ММВБ Акции
- наука
- нейронные сети
- облигации
- одураченные случайностью
- оптимизация
- оптимизация торговых систем
- опционы
- оффтоп
- оционы
- памм счета инвестиции
- паника
- пирамида
- ПИФы
- портфели
- Портфель
- портфельное инвестирование
- пузыри
- раздача
- рецензия
- Риски
- рэнкинг мосбиржи
- Сбербанк
- спекуляции
- статистика
- стоимостное инвестирование
- талеб
- теги не нужны
- теория игр
- торговая система
- торговые роботы
- трейдинг
- улыбка волатильности
- управляющая компания
- финанализ
- фундаментальный анализ
- фьючерс ртс
- Шарп
- шутка
- Экономика



















Какие инструментальные средства используете для расчета GARCH?
в качестве ограничений — положительная долгосрочная волатильность и положительная связь между локальной и будущей волатильностью.
Массив волатильности получаю через функцию, идентичную:
Более сложные модели дают плохие CV тесты. Поэтому, дабы не осложнять роботу жизнь пользуюсь пока самыми простыми.
так шо? нет в жизни счастья?....
Очень в тему топик. Можно сказать с языка сняли. Поэтому попробую задать свой вопрос здесь в виде комментария. Разрешите?
Итак, как мне в данный момент представляется вся эта история с стерхом ГАРХом:
п1. Наилучший прогноз цены — цена текущая. Окей.
п2. Дальше индустрия предлагает посмотреть ошибки нашего «прогноза». И почти сразу приходит к наблюдению, что величина ошибок на разных участках истории разная.
п3. Тогда предлагается попробовать моделировать волатильность. Например, моделью ГАРХ.
И вот тут у меня возникает вопрос: а в чем смысл?
Зачем пытаться прогнозировать волатильность ошибок из п1?
Чтобы в разные моменты озвучивать разную величину доверительного интервала?
Далее, просто зная о том, что волатильность кластеризована можно заниматься чем угодно — покупать опционы или строить «фильтр волатильности» для своих систем — это уже значения не имеет.
Можно подумать, что Максвелл, составляющий уравнения электродинамики, когда-либо думал о том зачем это нужно, и вообще мог прогнозировать то, что на его уравнениях будет, в конечном счете, построена вся современная промышленность (электродвигатели и пр.) и цивилизация (связь, ТВ и пр.).
Ну а если брать историю, то GARCH, как я понимаю, разрабатывалась конкретно под опционы и смысл её как раз в том, что Sharp рынка -> 0 и, в этом случае, единственный метод оценки опционов — оценка волатильности.
Если у вас Sharp -> 1, то вам эта волатильность вообще не нужна, достаточно просто прогнозировать МОЖ из пункта 1 и умножать на время.
Kot_Begemot, > "единственный метод оценки опционов — оценка волатильности".
В этих терминах это имеет смысл. Но тогда задачка становится чутка сложной: финрез моей торговли опционами зависит от эрви на внутридневном ТФ. То есть чтобы спрогнозировать свой завтрашний эрви мне следует строить ГАРХ на весь завтрашний день и суммировать. Только при этом точность прогноза 9-го бара будет примерно в 3 раза хуже точности прогноза первого бара. Которая скорее всего и так довольно паршивая...
Я бы так не сказал. Но даже если для вашего случая это так, то никто не мешает вам использовать внутридневную структуру волатильности (ARCH и т.п.) или просто перестраивать модель на каждом новом баре.
И так бы я тоже не выразился. Вполне приемлемая точность. С точки зрения, конечно, прогноза волатильности. Я не буду говорить что на этом можно или нельзя сделать деньги при помощи спекуляций, но точность вполне приемлемая для столь сложного объекта. То есть вход/выход модели — к этому у меня претензий нет.
Мне кажется, вы изначально рассматриваете рынок с точки зрения HFT, в то время как он в действительности создаётся и существует благодаря долгосрочным инвестициям и/или обороту реального сектора. При этом суть ваших претензий мне, честно, не понятна, так как они, по-сути, являются претензией к достигнутой при помощи этих же методов эффективности рынка.
Kot_Begemot, у меня «нет претензий». Есть вопросы, ответы на которые между ушей найти не удалось.
> "просто перестраивать модель на каждом новом баре"
Если мне нужно спрогнозировать эрви на завтра, а сделать это должен «завтра» с 00:00 до 10:00, то такой возможности нет. Придется строить цепочку прогнозов на все 14 баров одномоментно и принимать решения, исходя из этого.
То есть причина — последовательное развитие и усложнение статистических методов анализа финансовых временных рядов.
CBOE — чикагская биржа опционов — была открыта в 1973 году, то есть за 10 лет до первой ARCH модели. Связаны эти два события или нет — сказать сложно. Но то, что научное открытие (ARCH) вызывает интерес со стороны большего количества областей, несомненно стимулирует исследователя к работе.
ru.scribd.com/document/132007471/Engle-1982
Не проще ли уйти на следующий уровень и прогнозировать волатильность волатильности, она меняется куда реже, а мы все-равно торгуем волатильностью, куда пойдет БА нам все-равно.
Потом, что толку от vol of vol, если вы всё равно торгуете гамму? Да, вы конечно, можете собрать конструкцию, чувствительную к vol of vol, но вам станет это выгодно только в том случае, если вы сможете захеджировать (снять) её бОльшую чувствительность к vol. Насколько я понимаю сделать это практически невозможно. Но, быть может, я ошибаюсь.
Тем не менее, для того, чтобы строить коридор как у Е.Логунова, вам необходимо знать ошибку вашего прогноза. Евгений взял 15-40% то есть точность в районе 27.6% (средняя) и 83% (3 сигма).
Вот, по-сути, я об этом и пишу — точность примерно такая.
Далее всё зависит от выбора дов. вероятности и т.д.
Вы же хотите пойти другим путём, указав, что имеете преимущество над Е.Логуновым и можете сжимать и разжимать дов. интервал цен опционов во времени. Может быть. Только просчитать эти сжатия и растяжения будет ой как не просто.
Eugene Logunov, спасибо, но мне ещё рано туда.
Там разденут быстрее, чем успеешь сказать «дельта».