SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. Kot_Begemot
Непредсказуемость риска
- 07 ноября 2020, 09:23
- |
Привычное управление капиталом предполагает привычные подходы к риску, разработанные ещё для детерминированных финансовых инструментов, таких как акции и облигации :
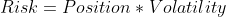
И даже если управляющий ошибется при расчете риска, то эта ошибка для риск-менеджмента в большинстве случаев не станет критичной :
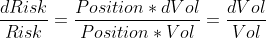
Другими словами, относительная ошибка контроля риска пропорциональна относительной ошибке оценки волатильности и на практике составляет не столь существенную величину — около 20%.
Но для стохастических финансовых инструментов, которые с вероятностью p превращаются в детерминированный финансовый инструмент, а с вероятностью (1-p) растворяются (например, это могут быть опционы), риск уже должен быть записан иначе :
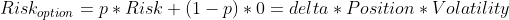
Теперь риск инвестиций в финансовый актив зависит не только от волатильности и вложенного капитала, как было ранее, но ещё и от некоторой неконтролируемой переменной дельта, характеризующей чувствительность опциона к изменению цен базового актива или использованное «плечо». Таким образом, получается, что инвестиции в опционы это не просто инвестиции, а инвестиции со стохастическим плечом и неконтролируемым риском.
В этом случае относительная ошибка оценки риска составит:
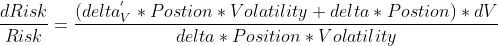
Или, с учётом того, что риск опционных конструкций в некотором приближении пропорционален их стоимости, запишем :
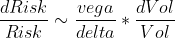
Теперь рассмотрим зависимость случайных величин delta и vega от случайного страйка на недельных опционах RI :
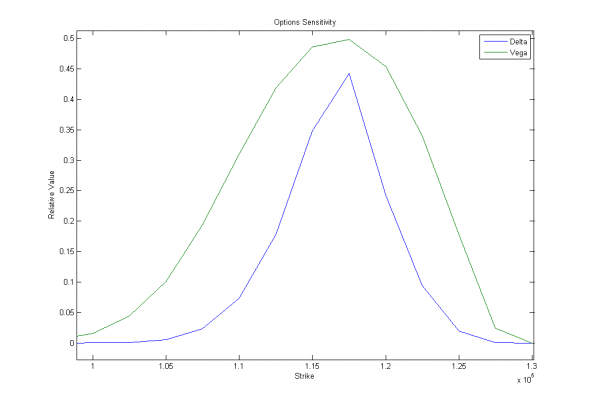
Иллюстрация. Дельта (вероятность превращения во фьючерс) и Вега (чувствительность премии к волатильности) недельных опционов RI в зависимости от страйка при цене базового актива 116 640 пунктов.
И их отношение, характеризующее коэффициент пропорциональности между относительной ошибкой контроля рисков и относительной ошибкой оценки волатильности:
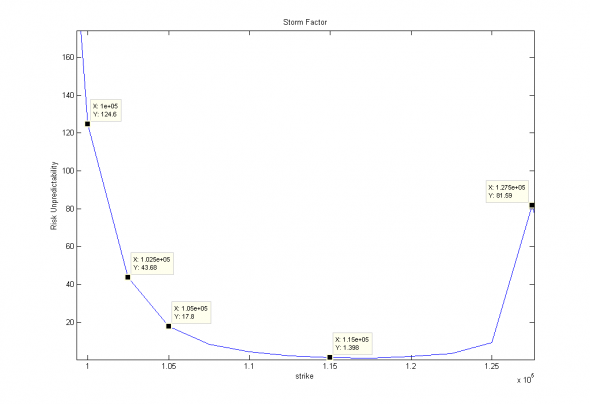
Иллюстрация. Возможные превышения рисков управляющим при относительной ошибке оценивания волатильности 1.
Видно, что даже если предположить максимальную ошибку оценки волатильности 50% (что вполне вероятно), то при продаже или покупке опционных «краев» можно легко превысить расчетные риски в 8 (105 000), 20 (102 500) и даже 60 раз (100 000). О каком контроле рисков здесь вообще может идти речь?
Ранее, симуляционное моделирование контроля рисков при торговле опционами показало схожие результаты:
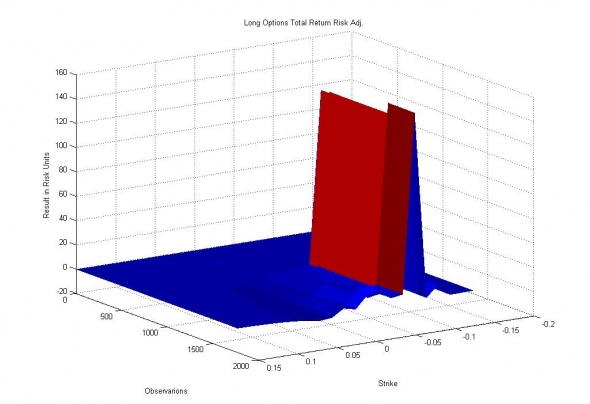
Иллюстрация. Реализованный риск при торговле опционами на индекс SP500, при ограничении риск-контроля 3 (превышение в 40 раз).
Опасность данного эффекта в том, что он приводит к редким, но фатальным просчетам, объясняющим неприменимость классических критериев Sharp и MDD при оценке управления портфелем опционов.
теги блога Kot_Begemot
- API
- cpp
- FORTS
- LUA
- Matlab
- NASDAQ
- open source
- Quik Lua
- S&P
- S&P500
- S&P500 фьючерс
- Vanguard Group
- VIX
- акции
- акции США
- алгоритмы
- алготрейдинг
- анализ временных рядов
- баффет
- волатильность
- Гордон
- доверительное управление
- долги
- игры
- инвестиции
- индекc
- интеграция
- искусственный интеллект
- Келли
- Книги
- книги о трейдинге
- корреляция
- кризис
- криптовалюта
- лудомания
- Марковиц
- матлаб
- машинное обучение
- ММВБ Акции
- наука
- нейронные сети
- облигации
- одураченные случайностью
- оптимизация
- оптимизация торговых систем
- опционы
- оффтоп
- оционы
- памм счета инвестиции
- паника
- пирамида
- ПИФы
- портфели
- Портфель
- портфельное инвестирование
- пузыри
- раздача
- рецензия
- Риски
- рэнкинг мосбиржи
- Сбербанк
- спекуляции
- статистика
- стоимостное инвестирование
- талеб
- теги не нужны
- теория игр
- торговая система
- торговые роботы
- трейдинг
- улыбка волатильности
- управляющая компания
- финанализ
- фундаментальный анализ
- фьючерс ртс
- Шарп
- шутка
- Экономика



















Я конечно, сам в этом топике мало что понял, но к нему попозже вернусь(может вечером или завтра), прочитаю комментарии.
то есть если покупать/продавать опционы на ЦС риски под контролем будут и все ок?
leverage губителен и в линейном инструменте, а тут еще и ось риска по веге.
Я в прошлом так не смог осилить задачу определения и управления этой неконтролируемой переменной дельта. Единственным решением (понимаю, что неидеальным) стала синтетика.
пусть фьючерс стоит x0 и на экспирацию выйдет с функцией плотности p(x+x0), где x — возможные отклонения от текущей цены.
Тогда стоимость Call опциона со страйком K составит :
Sum( p(x+x0) * (x+x0-K) ), по всем x+x0>K
Дельта опциона, соответственно, будет равна производной по этой сумме. Пренебрегая относительным изменением функции распределения p(x+x0) по x0, мы можем взять производную по этой сумме и получить :
дельта = Sum ( p(x+x0)*1+p'(x+x0)*(x+x0-K) ) ~= Sum ( p(x+x0) )
То есть это всё же некоторое приближение.
в размере премии?
Профит > 0.5*Vol
Risk ~= 0.3*Vol
Sharp> 16*0.5/0.3 = 26.
Kot_Begemot, рынок действительно «ошибается» в полтора раза, но Вы, во-первых, занизили оценку риска, во-вторых, непонятно откуда взяли множитель 16.
Итоговый шарп на порядок скромнее.
Собственно, Вы же всё видели на ИР2019.
Давайте предположим, что средняя переоценка опционов = x, тогда :
Price = 0.8*V (МБШ)
Profit = 0.8*x*V
E = 0.8*x*V/T
Risk=0.3*V
Risk/Day=0.3*V/T^0.5
Sharp = E/DailyRisk = 2.66*x/T^0.5
А годовой Sharp = 16*Sharp = 40 *x/T^0.5
Таким образом, x = 0.025*Sharp*T^0.5
Для пятидневных опционов (утро пятницы) и шарпа 2.5 (на порядок ниже), получается, что средняя переоценка соответствует 14% или около 200-250 пунктов на опцион RI.
По моим расчетам и наблюдениям эта оценка близка к действительности. И, если у вас получается в 3-4 раза больше, то скорее всего это уже ваша ошибка «в полтора раза», а не ошибка рынка. Присмотритесь.
Связка, собранная из двух некоррелированных опционов (экспирация обоих сразу невозможна), должна обладать риском :
R= ( 1/4*V^2 + 1/4*V^2 )^0.5 = 0.7*V
В действительности же, результат ближе к 0.6*V, но его вывод достаточно сложный для комментария.
Численное же моделирование , показывает, что при минимальном ДХ риск сокращается ещё в 2 раза и уменьшается далее с ростом частоты ДХ. Так, например, для 15 хеджей риск связки составляет 0.82 при волатильности (на экспирацию) 15^0.5 = 3.87. То есть 21% от волатильности. А риск без хеджирования подтверждается на уровне 58%.
По ссылке можно так же рассмотреть аналитическое приближенное решение, полученное без каких-либо дополнительных предположений.
«Белые» введены KarL$on'oм ни то как «теоретики» с «формулами», ни то как дельта-нейтральщики. Толком и не знает никто, но все поделились на два враждующих лагеря. Наверное эффект такой психологический, чтобы жизнь однообразной и скучной не была
в общем… утро субботы не прошло даром…
В этом смысле Смартлаб очень хорош — всё время давит научным авторитетом на ленивые мозги.
формула
N = LOG(1-C)/LOG(1-p)
додумана в моих темах
немыслимо давно
Логарифм Интегралыч
01 ноября 2020Какое-то странно ощущение, что название темы очень перекликается с фразой "Непредсказуемость случайного числа"...
ПС И от второй формулы dRisk/Risk кровь пошла из глаз… извините, дальше не могу читать.![]()