SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. Kot_Begemot
Критическая масса и критическое значение
- 24 мая 2021, 00:23
- |
Проведем небольшой тест — возьмем один случайный фьючерс, приращения которого представлены временным рядом случайных чисел, и набор случайных стратегий, представленный множеством N временных рядов случайных чисел (он же матрица признаков, фичей, пространство предикторов и т.д.) и попытаемся найти из этого большого набора тот признак, который будет лучше всего говорить нам когда покупать фьючерс, а когда продавать. Что это будет, мультипликатор P/E, фаза луны или MACD — не важно, главное чтобы на выходе получилась «идея» или, как ещё говорят, «грааль».
Хорошо известно, что случайная стратегия примененная к случайному инструменту даст случайное эквити, которое будет иметь гауссову плотность распределения коэффициента шарпа с математическим ожиданием 0 и среднеквадратичным отклонением
где L — число известных значений случайного фьючерса.
Это означает, что достаточно большое множество случайных стратегий (или случайных признаков), примененных к случайному фьючерсу абсолютно случайным образом окажутся способными достаточно хорошо описать любое поведение случайного фьючерса (отклика) в бек-, форвард-, голкипер-, кросс-, спринт- и всех прочих тестах… но только на истории.
Для того чтобы минимизировать риск отбора признака (стратегии) не имеющего никакой ценности в мат. статистике используется функция ошибок, связывающая вероятность реальной полезности признака и его прогностическую силу на исторических данных.
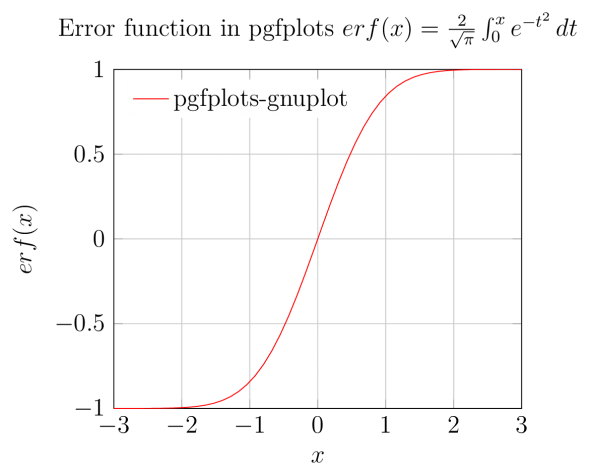
И обратная функция ошибок, позволяющая рассчитать критическое значение шарпа случайной эквити, при достижении которого мы можем утверждать, что с заданным уровнем доверительной вероятности альфа этот признак является полезным.
Таким образом, мы можем указать критерий отбора значимых признаков, при котором действительно значимыми окажутся более чем
где erfinv — обратная функция ошибок.
Но всё это хорошо, когда мы имеем одну стратегию и один признак. А если у нас их 100, или 1000, как это любят бигдата-сайентисты и различные количественные специалисты?
Рискнем предположить, что ни один из N независимых случайных признаков, не покажет шарп выше заданного критерия с вероятностью
Изобразим полученную зависимость для доверительной вероятности 90% и переменного числа признаков от 1 до 300:
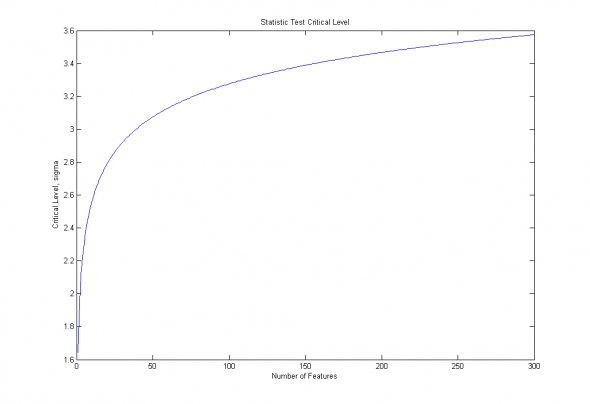
Рис. 1. Зависимость критического уровня от числа признаков, для доверительной вероятности 90%.
Особенно это опасно на данных небольшой размерности, когда незначительный рост размерности признакового пространства ведет к взрывному росту критических уровней статистической значимости.
Дополнительную сложность вызывает и само определение размерности признакового пространства в случае ненулевой коррелированности случайных признаков. Мы не будем мудрствовать, и оценим эффективную размерность «на глаз», то есть в первом приближении :
где С- корреляционная матрица случайных эквити, l-единичная вектор-строка.
Легко видеть, что при корреляции признаков 1, то есть когда, по-сути, мы имеем только один признак, — эффективная размерность стремится к 1, а при корреляции признаков равной нулю — к N.
Но мы, как настоящие дата-сайентисты, на этом не остановимся, а пойдем дальше, собрав из простых признаков-стратегий целый портфель. Легко показать, что портфель из стратегий взятых с весами
где бетта — вектор строка весов признаков (стратегий), С — корреляционная матрица случайных эквити.
C другой стороны, перебирая все возможные портфели, мы будем варьировать не только знаменатель, но и числитель, заставляя портфель перекладываться в менее прибыльные стратегии диверсифицирующие риски. Запишем приблизительное соотношение для оптимального портфеля, полученное из соображений пропорционального качеству взвешивания:
Следовательно, c учетом эффекта портфелизации, наш критический порог возрастает до:
Продемонстрируем справедливость оценок на примере авторегрессионных моделей броуновского движения :
MatLab side :
n=20;
x=randn(1000,1);
M=zeros(1000,n);
for i=1:n;
M(:,i)=[zeros(i,1);x(1:end-i)];
end;
a=(M'*M)\(M'*x);
r=(M*a).*x;
Mы будем искать медианное значение шарпа для AR(n) модели, такое которое с вероятностью 50% пройдет наш статистический тест:
Что для N=20 и бетта=1/N даст пороговое значение :
Проведем тест из 1000 испытаний aвторегрессионных моделей порядка N=20, построенных на различных реализациях белого шума:
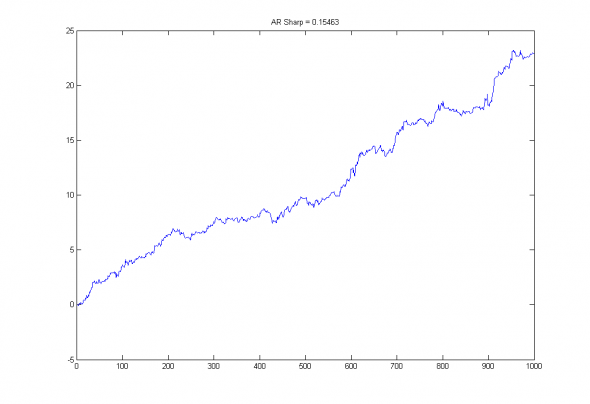
Рис2. Эквити и коэффициент шарпа случайной авторегрессионной модели порядка 20, построенной на белом шуме.
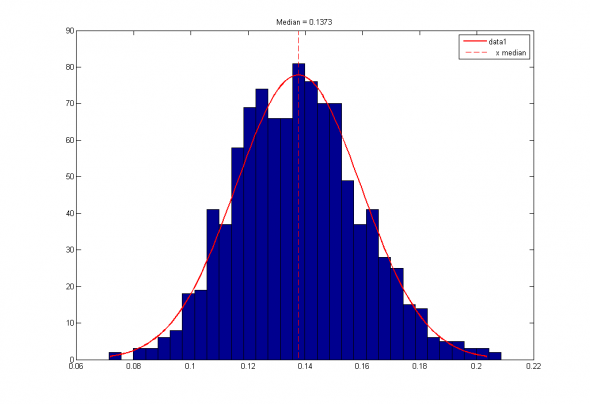
Рис 3. Распределение коэффициентов шарпов случайных авторегрессионных моделей порядка 20 и их медианное значение.
Видно, что полученная приблизительная оценка 0.1417 достаточно близка к эмпирическому значению 0.1373.
Таким образом, получается, что реальные статистические пороги для портфельных методов и всех без исключения методов MachineLearning находятся многократно выше «классических» Z- и T- тестов.
теги блога Kot_Begemot
- API
- cpp
- FORTS
- LUA
- Matlab
- NASDAQ
- open source
- Quik Lua
- S&P
- S&P500
- S&P500 фьючерс
- Vanguard Group
- VIX
- акции
- акции США
- алгоритмы
- алготрейдинг
- анализ временных рядов
- баффет
- волатильность
- Гордон
- доверительное управление
- долги
- игры
- инвестиции
- индекc
- интеграция
- искусственный интеллект
- Келли
- Книги
- книги о трейдинге
- корреляция
- кризис
- криптовалюта
- лудомания
- Марковиц
- матлаб
- машинное обучение
- ММВБ Акции
- наука
- нейронные сети
- облигации
- одураченные случайностью
- оптимизация
- оптимизация торговых систем
- опционы
- оффтоп
- оционы
- памм счета инвестиции
- паника
- пирамида
- ПИФы
- портфели
- Портфель
- портфельное инвестирование
- пузыри
- раздача
- рецензия
- Риски
- рэнкинг мосбиржи
- Сбербанк
- спекуляции
- статистика
- стоимостное инвестирование
- талеб
- теги не нужны
- теория игр
- торговая система
- торговые роботы
- трейдинг
- улыбка волатильности
- управляющая компания
- финанализ
- фундаментальный анализ
- фьючерс ртс
- Шарп
- шутка
- Экономика



















главное в физике — не пускать в нее математиков… а если пролезли, гнать ссаными тряпками))
Статистические гипотезы подразделяются на нулевые и альтернативные, направленные и ненаправленные.
Проверка гипотез осуществляется с помощью критериев статистической оценки различий. Критерии делятся на параметрические и непараметрические.
В случае очень больших отличий распределений признака от нормального вида, следует применять непараметрические критерии, т.е. рыночный ряд разбить по какому то свойству(к примеру — весь день растет, или падает, или стоит на месте) и про ранжировать заново а уже потом статистический вывод.Если Вы решаете задачу - Выявление различий в уровне исследуемого признака., то надо применять соответствующий метод.
P.S. Добавил демонстрацию AR-20 модели. Чтобы показать справедливость оценок.
Ошибка первого рода отвергли нулевую гипотезу в то время когда она верна.
В действительности же ни мне, ни вам ничего не понятно ни из эмпирического опыта (так как сознание это не просто отражение материальной действительности как опыт, это есть некоторое систематизированное отражение), ни, тем более, из здравого смысла. Здравый смысл вообще самая вредная штука, так как состоит сплошь и рядом из заблуждений (исторический факт такой) о том, что Земля плоская, Короли голубых кровей и т.п.
Физику отменять не надо. Но по прежнему не понятно, нафига доказывать очевидное, если в мире… трейдинга столько всего не очевидного).
А я всё просчитываю заранее и то, что просчитываю алгоритмизирую, чтобы точно знать как я торгую, как я страхую, что можно делать, а чего нельзя, что важно, а что — нет, где можно рискнуть и как именно построить (а это обычно требует точных расчетов) грааль. По-моему в этом и заключается любой профессионализм, разве нет?
— Есть такая штука как приоритизация — я не буду заморачиваться вещами, которые того не стоят в то время как есть те, от которых выхлоп будет намного интересней. Вещи с низким приоритетом всегда можно по лайту обработать: 2.5 % усилий — 25% выхлопа или типа того).
— Считать, анализировать, продумывать, просчитывать это далеко не всегда строить формулы и вот это вот всё.
Формулы расчета надежности ........
А вы просто взяли 90%.
Ни чего не смущает?
но понравилося, что Шарп стал 8,4 вместо 1,4…
корень квадратный — энто вверх моего математического аппарата на рынке..
а так все по простому по рабоче-крестьянски...-
цена выше средней скользящей цены на периоде -покупаем, цена ниже средней скользящей цены на периоде — продаем…
Алготорговля имеет смысл если
«приращения которого представлены временным рядом случайных чисел»!=True
Поэтому точка зрения Replicant_mih вполне адекватна.
Как определить, что этот индикатор существенно лучше, чем случайный поток нулей и единиц (плюс-минус единиц)?
А если индикаторов N и я выбираю лучший?
Можно строить доверительные интервалы по модели, аппроксимирующей реальную выборку, скажем гауссу, который имеет среднее и дисперсию, равные выборочной оценке.
Можно использовать монте-карло. Делать N серий, в серии выбирать лучшую. И таких серий 1000 или 1000000.
Рядом другой вопрос, а что проверять. Доху или доху/риск?
Как-то так.
«Как определить, что этот индикатор существенно лучше, чем случайный поток нулей и единиц (плюс-минус единиц)?»
Считаю что любая профитная стратегия построенная на прошлых данных это поиск повторяющихся паттернов (тот же моментум) в ценовом ряду. Да, паттерны могут перестать работать. Но даже то что они повторялись достаточное количество раз и достаточно длительное время чтобы мы на них накурвфиттили — с высокой вероятностью не случайно. Ведь чтобы паттерны повторялись какие то деньги должны были повторять одни и те же действия. В этом отличие от сферических ценовых рядов.
Давайте посмотрим с другой стороны — какова вероятность того что случайный поток даст приемлемую еквити даже на in sample? А на out of sample? Она видимо низкая. Значит индикатор выдавший приемлемую еквити уже с высокой вероятностью существенно лучше чем случайный поток?
А если я использую 2 индюка одновременно. А если три. А если индюки не двузначные, а многозначные. Где сидит мера между переподгонкой и прорывом?
Насчет паттернов. Тут трудности с терминологией. Например в свечном анализе какой-нибудь набор свечей «три зеленых засранца» — паттерн. А цена выше скользяшки — паттерн? А пробой канала паттерн?
Есть же oos. Чем больше индюков тем хуже устойчивость. Блекбокс с кучей индюков дает неустойчивый курвфит. Будем пробовать по эквити (на in sample как у автора) пытаться определить уровень неустойчивости?
«Насчет паттернов. Тут трудности с терминологией. Например в свечном анализе какой-нибудь набор свечей «три зеленых засранца» — паттерн. А цена выше скользяшки — паттерн? А пробой канала паттерн? „
Я в широком смысле имел в виду любые неэффективности. Например движение рубль/доллара на дневной сессии дает ожидание на следующий день, это аномалия. Строим на этом стратегию. Подгонка? Конечно. Т е любая стратегия это подгонка под какие либо неэффективности на истории.
А как вы по OOS определяете уровень устойчивости? Смею предположить, что никак, нет?
Можно сделать и метрику, скажем Шарп/Сортино на oos Vs in sample или там угол наклона эквити (с нормировкой на волатильность).
Если эффект наблюдается 10 лет кряду, причем простой-препростой, значит, на его счет не надо париться. Он может со временем исчезнуть, что надо отдельно мониторить. И самое простое — мониторить именно сам эффект, а не сложную ТС, в которой, кроме одного эффекта поневоле наверчено будет еще хоть что-то.
Эффект можно мониторить и по метрикам и по всем стратегиям которые его используют.
Но если система накурвфичена из икс факторов а метрики по эквити без погружения в факторы это не очень практически выглядит.
Все имхо.
Идти нужно от предполагаемых эффектов влияния чего-либо на будущую цену. И брать только стратегии относительно этого 'чего-либо'. Если предварительные прикидки на разных инструментах и отрезках дают положительную корреляцию.
И для этого 'чего-либо' строить всё вышеописанное.
Возникла статистика так измеренных движений. Перешёл к реверсной системе на её основе. Она околонулевая с учётом комиссии.
Сильно позже «открылось» как пропускать большинство переворотов. Негаданно пришёл к трендовой системе таким образом.
Берёте свою систему и участки на ней хорошие и минусующие. Пытаетесь найти на каждом участке ключевой признак, на него влияющий. Чтобы его значения значимо отличались.
Потом пытаетесь найти универсальную границу по значениям этого признака, чтобы успевать перестраивать систему с одного типа участка на другой. Если удастся, то хорошие участки снизят свои результаты меньше, чем улучшат свои результаты минусующие.
а от длинны данных. 1 год или 10. вероятность подгонки будет зависеть?