Блог им. AntonStupin
Немного о фракталах и множестве Мандельброта
- 08 ноября 2022, 13:40
- |
Антон Ступин
Что породило само понятие фрактал? Изучив некоторое количество материалов об истории фрактала, я пришел к выводу, что это понятие создано все тем же неизменным двигателем человеческого прогресса и эволюции — любопытством.
В этот раз любопытство сфокусировало внимание человека на математическом описании окружающего мира. Именно стремление к познанию создало понятие фрактал. Человек стремится описать ту реальность, которая есть вокруг него. Новые открытия — это новые элементы пазла, которые добавляют целостность картине реальности.
Термин фрактал появился относительно недавно — в 1975 году математиком Бенуа Мандельбротом, в честь которого назван самый популярный фрактал. Но, прежде чем перейти к рассмотрению множества Мандельброта, окунемся в историческую сводку и постараемся выделить основную проблему, которая сподвигла Бенуа к исследованию и созданию фрактальный геометрии.
 Бенуа Мандельброт (1924-2010)
Бенуа Мандельброт (1924-2010)
До создания фрактальный геометрии, истинной являлась Евклидова геометрия (да, та самая, которую мы изучали в школе) и именно она на протяжении более 2000 лет служила базой для описания физического мира (прямые линии, углы, треугольники, квадрат и т.д — это все из геометрии Евклида).
 Евклид (около 300 лет до н.э) — древнегреческий математик
Евклид (около 300 лет до н.э) — древнегреческий математикЕсли мы посмотрим на то, что нас окружает, то условно сможем разделить все на две части: то, что создано человеком и то, что создала природа. То, что построено человеком — построено по постулатам евклидовой геометрии (круги, треугольники, квадраты и т.д.). Но чем как описать деревья, горы, реки? Как описать все то, что создала природа? Да, конечно, можно описать все, используя простые фигуры, меняя их масштаб и положение относительно друг друга (что-то мне подсказывает, что мир бы выглядел как в игре Майнкрафт). Но, если серьезно, то попытка описать мир таким принципом — это лишь попытка смоделировать (построить модель), но не описать все так, как оно есть.
Именно желание описать мир, с его, казалось бы, несовершенством линий и попытка придать всему этому хаосу некие закономерности и привело к созданию понятия фрактал и фрактальный геометрии.
Определение фрактала. Примеры.
Определение из интернета «Фрактал — множество, обладающее свойством самоподобия». Звучит сложно. Попробую объяснить, используя некоторые высказывания, относительно фракталов:
- Фрактал — самоподобная сложная фигура;
- Фрактал — элемент, повторяя который бесконечное количество раз, мы получим тот же/подобный элемент другого масштаба;
- Фрактал строится за счет многократного повторения (математики называют этот процесс "итерацией");
- Целый объект практически полностью совпадает с частью себя самого. Целые имеют ту же форму, что одна или более частей;
- Есть фигура и правило, по которому эта фигура дублируется относительно друг друга.
Как правило, итерация это многократное повторение простого действия. Фракталы были и до множества Мандельброта, но он описал эту теорию наиболее комплексно.
Чтобы упростить понимание фрактала: да, как сказано выше, природа очень самобытна и нелинейна, но она состоит из подобных элементов. Возьмем самый распространенный пример фрактала в природе — дерево. Оно состоит из подобных элементов: меленькая веточка подобна ветки крупнее и т.д.


 Лист папоротника
Лист папоротника Дельта реки
Дельта реки
Ниже приведем примеры фракталов с множественным повторением какого-то простого действия (итерацией):
- Кривая Гильберта
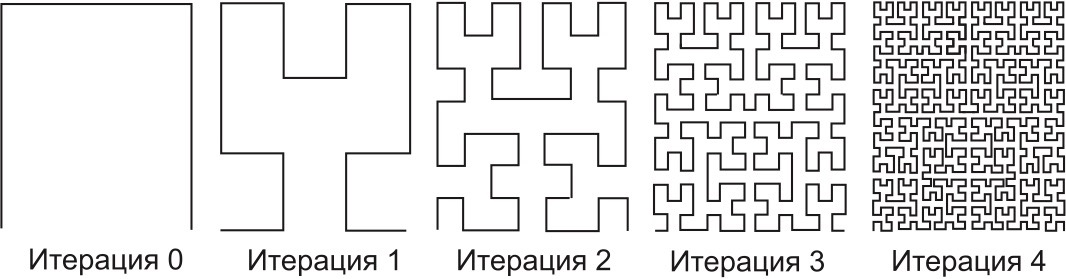 1891 г.
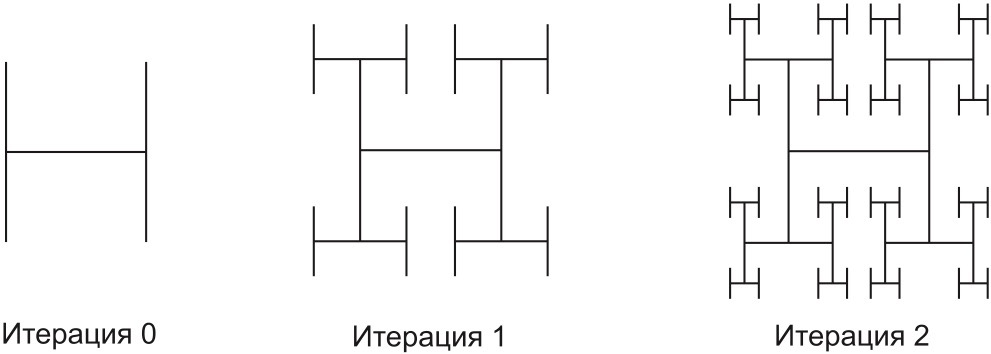
1891 г.2. Н-фрактал (конечные точки буквы «Н» заменяем на «Н» и так до бесконечности)
3. Треугольник Серпинского (внутри треугольника строим перевернутый треугольник и так до бесконечности)
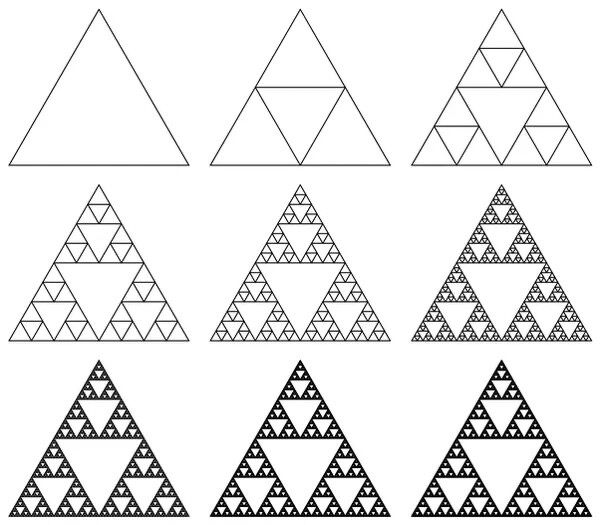 1915 г.
1915 г.
4. Кривая Коха (делим сторону равностороннего треугольника на 3, среднюю часть заменяем на равносторонний треугольник и так до бесконечности с каждой стороной каждого треугольника)
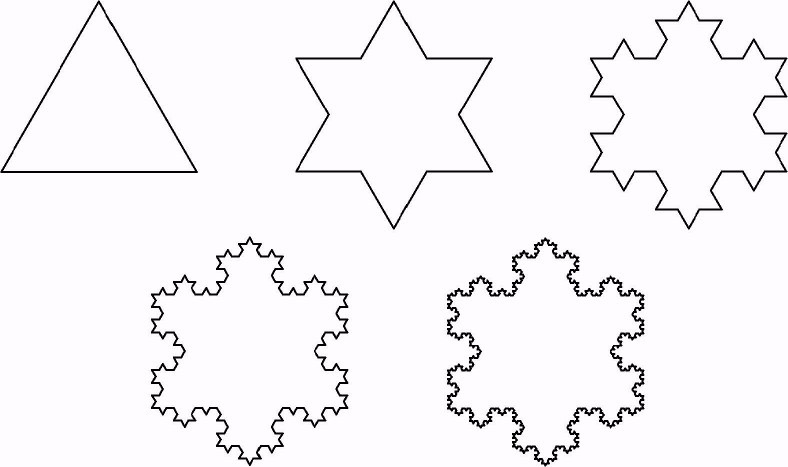 1904 г.
1904 г.
Как мы видим, что все сложные фигуры складываются из самоподобных элементов, с помощью простого правила.
Множество Мандельброта.
Повторюсь, что итерация простых элементов для построение целостной сложной фигуры были и до работы Бенуа Мандельброта. Увеличение вычислительной мощности компьютеров позволило достичь огромного числа повторений, что позволило ученому достичь такой глубины в понимании фрактальности мира:
 Множество Мандельброта (1975 г.)
Множество Мандельброта (1975 г.) Увеличенный масштаб множества Мандельброта
Увеличенный масштаб множества Мандельброта Масштабируя множество…
Масштабируя множество…Попутешествовать по завораживающему множеству Мандельброта можно по следующим ссылкам:
www.michurin.net/online-tools/mandelbrot.html
Как бы вы не меняли масштаб, вы всегда будете видеть похожие на себя фигуры. Это и есть ключевой признак фракталов — самоподобие при изменении масштаба.
Принцип построения модели:
В основе модели, как и писал раньше, лежит итерация (многократное повторение). В случае множества Мандельброта — это решение уравнения.
Оно выглядит так:
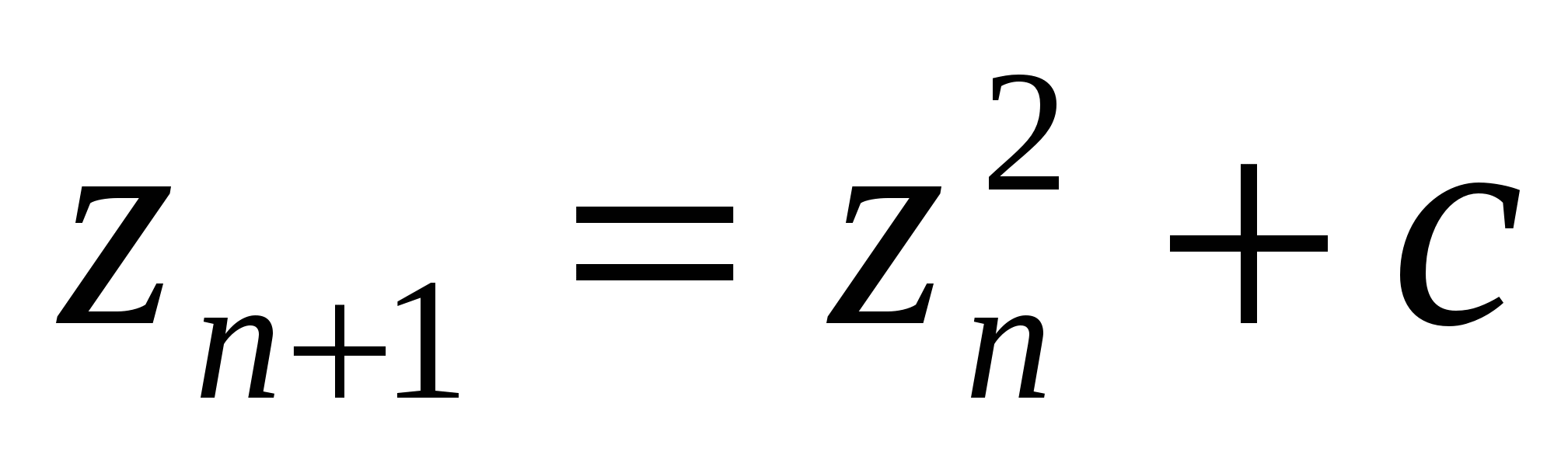 уравнение Множества Мандельброта, где С — комплексное число
уравнение Множества Мандельброта, где С — комплексное числоДля математика выглядит достаточно просто, но есть нюансы. Не будем вдаваться в подробности, попробуем пошагово раскрыть суть построения множества:
Чтобы определить, входит ли число в множество Мандельброта, нужно принять Z за ноль (О) возвести в квадрат и сложить с нашим числом. Полученное число Z — заново подставляем в уравнение и складываем с числом, которое тестируем. Уравнение решается и полученное решение снова подставляется в уравнение. Уравнение заново решается. Итерация! Множественное повторение решений одного и того же уравнения. Если при решении мы видим, что значение Z сильно увеличивается (стремится к бесконечности), значит изначальное число не подходит. Если же Z колеблется в пределах одного значения, значит выбранное число входит в множество. Далее полученные значения отмечают на плоскости. Уравнение решается огромное количество раз и в итоге получается графическое изображение множества Мандельброта (его мы видели выше).
P.s можно еще посмотреть что такое комплексные числа — они имеют большое значение для построение модели.
До 1975 года, фракталы встречались в истории время от времени, но после работы Бенуа Мандельброта, изучение фракталов начало приобретать массовый характер, все больше интегрируясь в мир. Изучение фракталов вызвало новый виток в изучении разных сфер жизни: в компьютерной графике, в передаче данных, в радиотехнике, в производстве, в работе мозга, в движениях человека, в росте живых существ и многом другом.
Представьте, насколько упрощается построение графических моделей, зная, что они самоподобны и вычисляются по одной простой формуле. Насколько становиться проще кодирование и передача информации, когда есть понимание, что их можно «сжать» по определённой фрактальный закономерности. И насколько понятней становится эволюция живых существ, когда мы можем найти фракталную модель их развития.
Фракталы в тейдинге.
Тема фракталов сложна и интересна, но как же она соотносится с торговлей на бирже? Думаю, что идея также проста: попытка описать и упорядочить казалось бы хаотичное и нелинейное движение цены, и найти в нем определенные закономерности.
Тема фракталов достаточно молода, но одно знаем точно, что ее глубина и охват — это «черная дыра» с огромным количеством идей и возможный векторов применения.
Первое, что мы можем выделить — это подобие графиков движения цены, вне зависимости от инструмента, таймфрема (временного масштаба). Разумеется, что найти абсолютно похожие участки крайне сложно, но ключевое свойство фрактала — это самоподобие, а не идентичность. А найти регулярные и подобные структуры в колебаниях цены — это уже более реальная задача.
Получается, что рынок, как минимум, имеет фрактальные свойства. Само наличие закономерностей в движении говорит об этом.
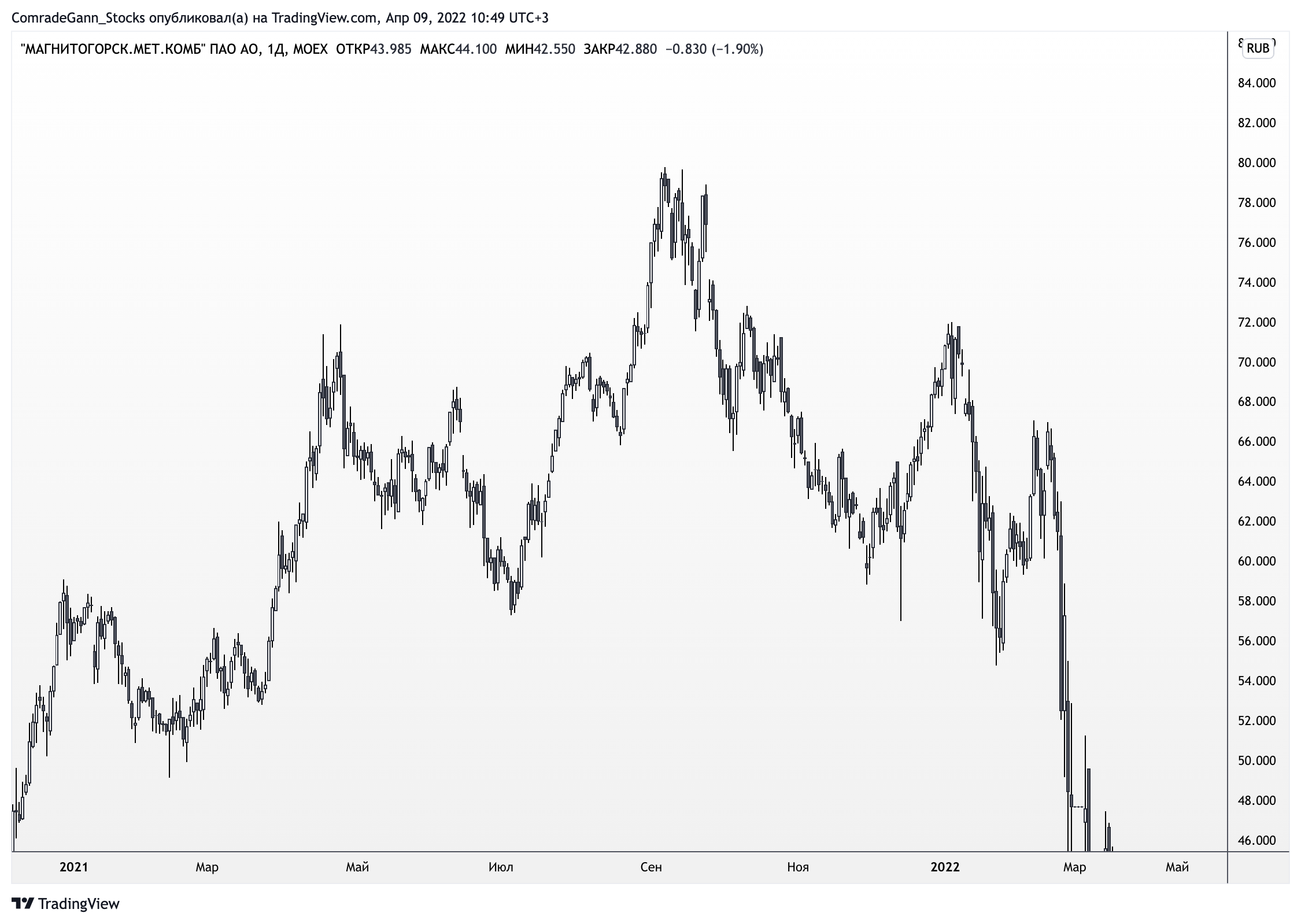 Фрактальное самоподобие на примере #MAGN (Магнитогорский металлургический комбинат)
Фрактальное самоподобие на примере #MAGN (Магнитогорский металлургический комбинат)Поиск закономерностей в движении цены, похожих ценовых моделей/паттернов (фракталов) — как одно из направлений, в которое можно углубиться.
Волны Элиота — также определенная фрактальная закономерность в движении цены
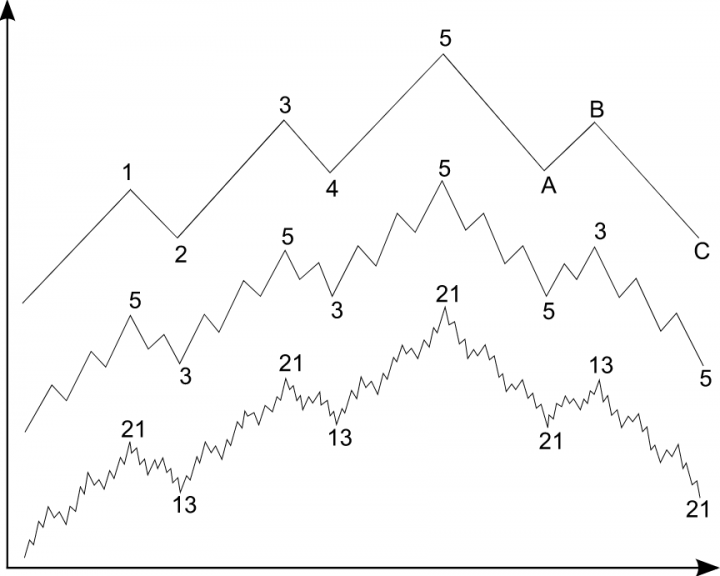 Каждая часть графика делится по определенной закономерность на самоподобные части.
Каждая часть графика делится по определенной закономерность на самоподобные части.
Что еще интересного можно найти на основе модели Мандельброта?
К примеру, можно взглянуть на соотношение частей этого фрактала:
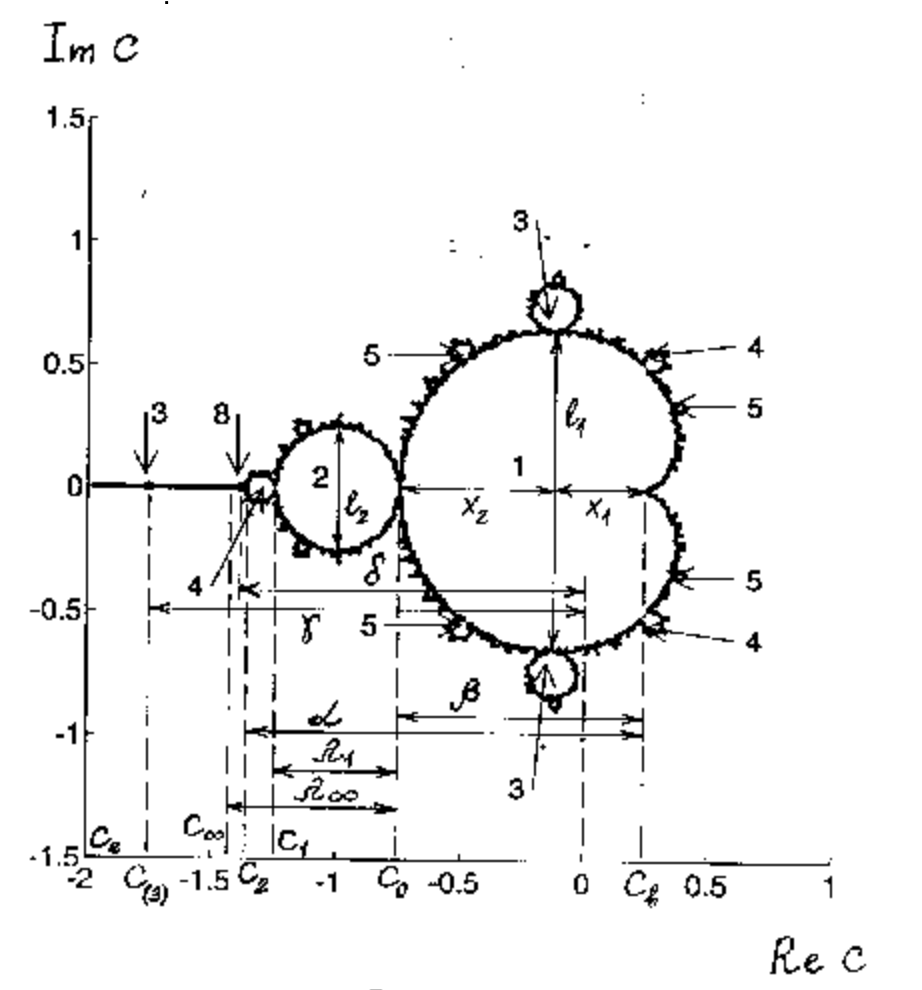
Фрактальную теорию тесно связывают с принципом золотого сечения и числами Фибоначчи. Опять же, не будем вдаваться в сложные математические вычисления и доказательства.
Нас тут интересует, что определенное соотношение частей и сторон множества
Мандельброта соответствуют принципам золотого сечения и чисел Фибоначчи.
А это уже совсем другая история...
Множество Мандельброта — это удивительный мир фракталов, возможности которого, по большей части, не изучены. Но, безусловно, изучение этого направления — это «окно» в мир новых теорий и концепций.
t.me/ComradeGann
теги блога Антон Ступин
- Aalibaba Group
- Alibaba
- Alibaba Group
- BABA
- Bonds
- FAANG
- gazp
- GAZP Газпром
- Gazprom
- Hang Seng
- Hang Seng Index
- IMOEX
- NASDAQ
- NVTK
- RGBI
- RTSI
- S&P500
- Sber
- sberbank
- spx
- SPX 500
- VTBR
- Xiaomi
- Xiaomi Inc
- акции
- Акции РФ
- акции США
- алибаба
- аналитика
- банки
- бонды
- Бонды США
- газ
- Газпром
- Ганн
- германия
- гонконгская биржа
- гособлигации
- гособлигации РФ
- гособлигации США
- дивидендная политика
- ЕС
- ЕЦБ
- ЕЦБ гособлигации
- золото
- Илон Маск
- инверсия
- инверсия кривой доходности
- индекс RTSI
- Индекс ММВБ
- индекс РТС
- Индекс МБ
- индекс РТС
- Индекс ртс прогноз
- инфляция
- инфляция в США
- Китай
- китайские акции
- Китайский фондовый рынок
- кризис
- Маск
- металлурги
- металлургический сектор
- ММВБ
- ММВБ Акции
- МосБиржа
- насдак
- Новатэк
- Облигации
- облигации США
- офз
- полюс
- Полюс Золото
- рецессия
- Рецессия в США
- Россия
- РТС
- РФ
- санкции
- сбер
- сбер преф
- сбербанк
- Сбербанк преф
- Северсталь
- сша
- твиттер
- технический анализ
- технологические компании
- тинькофф банк
- торговые сигналы
- трежериз
- трежерис
- трежерис США
- трейдинг
- форекс
- фьючерс mix
- фьючерс ртс
- Яндекс



















Тут игнорируется самая простая вещь. В природе каждый фрактал имеет под собой некий физический процесс. Образно говоря, природа создает листья и ветки дерева по одному и тому же алгоритму, просто в этом алгоритме идут одни и те же повторяющиеся итерации.
На рынке нас интересуют алгоритмы маркетмейкера. Они тоже состоят из итераций. Но алгоритмов то много. Редкий начинающий маркетмейкер пользуется одни и тем же алгоритмом.
smart-lab.ru/profile/Collapse/