Могут ли машины определять время на рынках? AQR.

Перевод исследования от AQR.

Сложности в прогнозировании доходности

Краткое содержание

Методы машинного обучения могут быть использованы для улучшения стратегий рыночного тайминга путем выявления нелинейности между переменными-предсказателями (т.е. сигналами) и доходностью. Чтобы выявить нелинейность, необходимо оценивать сложные модели, т. е. модели, в которых количество переменных-предсказателей больше, чем количество наблюдений за временными рядами доходности. Более сложные модели лучше выявляют истинные нелинейные взаимосвязи и, следовательно, обеспечивают более высокую эффективность стратегии рыночного тайминга. Этот результат «достоинства сложности» подтверждается на трех практических приложениях, связанных с рыночным таймингом: тайминг рынка акций, рынка облигаций и стоимостного фактора. Улучшения в работе реальны, но скромны, что согласуется с мнением о том, что машинное обучение, применяемое для прогнозирования доходности, приводит к эволюционному, а не революционному росту благосостояния.

Содержание

• Введение и основные положения
• Каковы возможные нелинейности в ожидаемой доходности?
• Почему более сложные модели работают лучше?
• Звучит здорово в теории, но работает ли это на практике?
• Достоинство сложности не является лицензией на дата-майнинг
• Заключительные мысли и будущие исследования

Введение и основные положения

Методы машинного обучения процветают в средах с высокой предсказуемостью и большими объемами данных. В целом, более крупные и сложные модели, то есть модели, в которых количество объясняющих переменных (предикторов) значительно превышает количество наблюдений зависимой переменной, показывают наилучшие результаты вне выборки. Это подтверждается точной языковой моделью GPT-3, использующей 175 миллиардов параметров, и различными другими моделями обработки изображений и естественного языка, которые используют астрономические параметры для точного соответствия обучающим данным и при этом показывают наилучшие результаты вне выборки.

В отличие от вышеописанных сред, финансы имеют низкую предсказуемость и небольшой объем наблюдений за временными рядами, что позволяет предположить, что небольшие, простые модели — не сложные модели машинного обучения — лучше всего подходят для приложений, связанных с определением времени выхода на рынок. Однако новые исследования ставят под сомнение этот принцип примитивности. Ожидаемая доходность, скорее всего, нелинейна по отношению к базовым переменным-предсказателям (т. е. сигналам), и небольшие простые модели рыночного тайминга упускают эту важную взаимосвязь. Большие, сложные модели способны уловить нелинейность и обеспечить лучшую эффективность рыночного тайминга. Более того, более сложные модели лучше работают вне выборки — так называемое «достоинство сложности».

Каковы возможные нелинейности в ожидаемой доходности?

Давайте начнем с конкретного примера прогнозирования доходности, демонстрирующего, как простая линейная модель может отличаться от более сложной нелинейной.

Предположим, что ожидаемая доходность определяется двумя сигналами — оценками (т.е. стоимостью) и краткосрочными показателями (т.е. импульсом). Когда оценки низкие (т.е. дешевые), а краткосрочные показатели хороши, ожидаемая доходность выше средней. На рисунке 2A эта зависимость изображена линейно. Но что если существует дополнительное влияние на ожидаемую доходность, когда оценки находятся на экстремальных уровнях — так называемая «глубокая стоимость»? Эта нелинейность показана на рис. 2Б. Можно включить дополнительные нелинейности между сигналами и доходностью, например, чрезмерное влияние на доходность, когда экстремальные оценки и импульс совпадают, т. е. рынок чрезвычайно дешев и имеет необычно высокие краткосрочные показатели (Рисунок 2C).

Почему более сложные модели работают лучше?

Сложные модели прогнозирования доходности лучше отражают реальность, улавливая нелинейность между сигналами (G) и будущей доходностью ®. На практике нелинейные связи неизвестны и должны быть оценены. Это можно сделать, оценив большую сложную линейную модель, в которой P новых переменных-предсказателей (S) создаются путем нелинейных преобразований исходных сигналов (G). См. Рисунок 3.

Сколько нелинейных преобразований исходных сигналов должно использоваться в эмпирической модели, т. е. должно ли P быть маленьким или большим? Если мы сначала сфокусируемся на цели ожидаемой доходности при рыночном тайминге, то более сложная модель с большим P будет лучше приближать модель прогнозирования истинной доходности. Как следствие, более сложные модели рыночного тайминга с более высоким P обеспечивают более высокую ожидаемую доходность. Это согласуется с рисунком 4, на котором показана ожидаемая доходность стратегии рыночного тайминга в зависимости от сложности модели ©. C равно количеству переменных-предсказателей в модели (P), деленному на количество наблюдений временного ряда (T). Если C меньше единицы, то мы находимся на знакомой нам статистической территории с большим количеством данных (T), чем переменных-предсказателей (P). Можно использовать стандартную регрессию по методу наименьших квадратов. Когда C больше единицы, существует бесконечное число решений задачи наименьших квадратов. В результате для оценки модели ожидаемой доходности необходимо использовать методы регуляризации, такие как множественная регрессия. Множественная регрессия вносит погрешность в прогноз ожидаемой доходности за счет уменьшения. В чистом виде ожидаемая доходность становится все сложнее, поскольку преимущества более точного приближения к истинной модели преобладают над издержками, связанными с ростом смещения из-за усадки.

Эффективность рыночного тайминга основывается не только на ожидаемой доходности. Доходность должна быть скорректирована с учетом риска. Хотя интуитивно может показаться, что более сложные модели обеспечивают более высокую ожидаемую доходность, не очевидно, что они могут делать это с разумным уровнем риска. Сложные модели прогнозирования доходности — модели с небольшим количеством точек данных и большим количеством параметров — очень трудно оценить, что увеличивает волатильность стратегии рыночного тайминга. Это явление наблюдается на Рисунке 4, когда C≤1. Когда количество переменных-предсказателей приближается к количеству наблюдений временного ряда, бета-параметры модели оцениваются неточно, и волатильность стратегии рыночного тайминга возрастает. Однако по мере усложнения модели методы регуляризации множественной регрессии способны определить набор бета-факторов, которые соответствуют данным и могут быть оценены с высокой точностью (т. е. с малой дисперсией). В результате коэффициент Шарпа рыночного тайминга растет с увеличением сложности модели, когда C больше единицы — так называемое достоинство сложности применительно к рыночному таймингу.

Звучит здорово в теории, но работает ли это на практике?

До сих пор мы концентрировались на теории, объясняющей, почему более сложные модели прогнозирования доходности обеспечивают лучшую эффективность стратегии рыночного тайминга. Теперь давайте применим теорию к трем практическим проблемам, связанным с рыночным таймингом: тайминг рынка акций, тайминг рынка облигаций и тайминг фактора стоимости. Можно ли с помощью сложных моделей определить время на этих рынках и факторах? Да.

Тайминг фондового рынка

Наша модель прогнозирования доходности акций использует 15 макроэкономических и финансовых сигналов рынка, изученных в знаменитой работе Гояла и Уэлча (Goyal and Welch (2008)) о прогнозировании доходности (см. Рисунок 5). Чтобы выявить нелинейные связи между сигналами и будущей доходностью, мы оцениваем 12-месячную скользящую множественную регрессию с 12 000 переменных-предсказателей (т. е. сложность C составляет 12 000/12 = 1 000). Зависимой переменной является избыточная доходность акций США с 1927 по 2020 год, а 12 000 переменных-предсказателей формируются путем нелинейных комбинаций 15 исходных сигналов Гояла-Уэлча (GW). Вес нашего портфеля рыночного тайминга равен прогнозируемой доходности, полученной в результате сложной 12-месячной скользящей множественной регрессии. Когда прогнозируемая доходность положительна, мы открываем длинные позиции, а когда прогнозируемая доходность отрицательна, мы открываем короткие позиции.

Мы также построили «простую» модель тайминга, которая аналогичным образом открывает длинные или короткие позиции на прогнозируемую доходность, полученную в результате 12-месячной скользящей линейной регрессии доходности рынка на исходные 15 необработанных сигналов-предикторов GW.

Вневыборочные показатели рыночного тайминга с использованием нашей сложной модели представлены на рисунке 5. Стратегия генерирует коэффициент Шарпа почти 0,5. Большая часть результатов не может быть объяснена статическим воздействием на рынок: коэффициент оценки (он же альфа-коэффициент Шарпа) превышает 0,3 при t-статистике почти 3. В то время как пассивный рынок имеет отрицательный перекос, стратегия рыночного тайминга имеет положительный перекос. Другими словами, стратегия генерирует привлекательную доходность с поправкой на риск, не подвергаясь воздействию нечастых, крупных хвостовых событий.

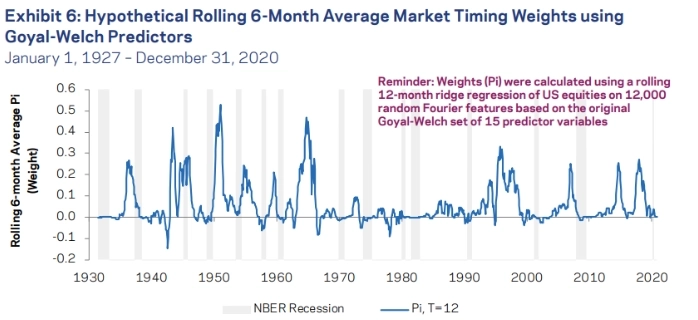
Для большей прозрачности сложной модели рыночного тайминга в рис. 6 приведены графики весов портфеля рыночного тайминга и рецессий NBER. Стратегия рыночного тайминга позволяет избежать 14 из 15 рецессий. Исключением является 8-месячная рецессия 1945 года. Интересно отметить, что стратегия эффективно работает только в длинную позицию, выходя в длинную позицию между рецессиями и примерно выходя из рынка во время рецессий.

Тайминг на рынке облигаций

Мы повторили упражнение из предыдущего раздела с одним изменением: зависимой переменной теперь является избыточная доходность 10-летних казначейских облигаций США. Вневыборочные показатели тайминга рынка облигаций с использованием нашей комплексной модели представлены на Рисунке 7. В соответствии с результатами, полученными при выборе времени для рынка акций, стратегия дает коэффициент Шарпа 0,3. Ни один из показателей не может быть объяснен статическим воздействием на рынок: коэффициент оценки также равен 0,3 при t-статистике 2,4. Стратегия синхронизации рынка облигаций также имеет положительный перекос.

Тайминг фактора стоимости

Наконец, мы переходим от тайминга традиционных премий за риск к таймингу одной из самых известных альтернативных премий за риск — фактору стоимости Фама-Френча (т. е. HML). Здесь все точно так же, как и в предыдущих разделах, за исключением того, что HML является нашей зависимой переменной. Результаты по HML схожи с теми, что были получены при тайминге рынка акций и облигаций. Стратегия тайминга HML генерирует коэффициент Шарпа 0,4 и коэффициент оценки с t-статистикой 3,4 и положительным перекосом (Рисунок 8).

Достоинство сложности не является лицензией на дата-майнинг

Большие, сложные модели, безусловно, могут помочь в определении времени на различных рынках и факторах. Однако достоинство сложности не является лицензией на введение в регрессию любой предикторной переменной. Очень важно, чтобы исходные сигналы были связаны с истинной нелинейной моделью ожидаемой доходности. Включение сигналов, не имеющих связи с истинной ожидаемой доходностью, ухудшает эффективность рыночного тайминга, как показано на Рисунке 9. Если мы используем более раннюю комплексную модель прогнозирования доходности акций с базовыми 15 переменными-предикторами GW, мы достигаем коэффициента Шарпа для рыночного тайминга 0,47. Когда мы включаем «шумные» переменные-предсказатели наряду с исходными 15 переменными GW, эффективность стратегии рыночного тайминга быстро снижается. Включение всего одной «шумной» переменной-предсказателя снижает эффективность почти на 50%.

Заключительные мысли и будущие исследования

Использование небольших, простых моделей прогнозирования доходности для определения времени рынка упускает нелинейные связи между переменными-предсказателями и будущей доходностью, оставляя деньги на столе. Большие, сложные модели преодолевают это ограничение, лучше оценивают истинную модель ожидаемой доходности и генерируют лучшие показатели маркет-тайминга — так называемое достоинство сложности. Принцип «достоинство сложности» подтверждается на примере тайминга рынка акций, рынка облигаций и стоимостного фактора. Коэффициент Шарпа при рыночном тайминге, скорректированный на статическую экспозицию, находится в районе 0,3. Таким образом, повышение эффективности от внедрения сложных моделей является реальным, но скромным, что согласуется с мнением о том, что машинное обучение, применяемое для прогнозирования доходности, приводит к эволюционному, а не революционному росту благосостояния. Хотя в данной работе основное внимание уделено временным рядам и применению рыночного тайминга, достоинство сложности также применимо и к формированию многофакторных портфелей. Например, рассмотрим следующие три популярных фактора выбора акций: стоимость, импульс и низкий риск. Какой портфель с наивысшим коэффициентом Шарпа можно создать с помощью этих трех факторов, и можно ли существенно улучшить этот результат, создав дополнительные факторы, которые являются нелинейными комбинациями исходных трех сигналов? Ответ на последний вопрос утвердительный — еще одна поперечная вариация достоинства сложности. Могут ли машины создавать лучшие многофакторные портфели? Да. Дальше будет больше.