19 ноября 2014, 00:25
Ход конем (ч.2.), или кое-что о фракталах
Как-то однажды от корки до корки прочел суперкнигу Мандельбро(т)’а где он собственно и ввел это понятие, и уже тогда некоторые из его кривых мне показались странно знакомыми. После этого талмуда Билл Вильямс кажется немного смешным. Но это все присказка, а я обещал начать от большого к малому:
Ну так вот, пусть не было ничего и вдруг — большой взрыв, ака Большое Ценовое Колебание (вообще даже не суть что это будет, неожиданно охренительные дивиденды, или ужасающая новость)
Фишка в том, что вероятность второго подряд большого движения, но в обратном направлении крайне мала (хотя, конечно и не нулевая). Вероятность движений среднего диапазона – несколько выше, но самая большая вероятность у маленьких движений.
Для компенсации одного мощного движения потребуется множество мелких, направленных в одну, да еще и в противоположную сторону, или несколько средних. При всем при этом, вероятность того, в какую сторону (вверх или вниз) будет направлено каждое из маленьких или средних движений равна почти 1/2 (если не учитывать 5% нулевых приращений цены). Иными словами, одно большое движение, скорее всего, полностью не компенсируется, до появления нового движения того же размера. А в идеальном случае так и вовсе не компенсируется – сумма всех мелких движений будет близка к нулю.
Рынок (да и вообще любой природный процесс) по моему скромному мнению развивается кризисами, а идеальный кризис выглядит примерно так.
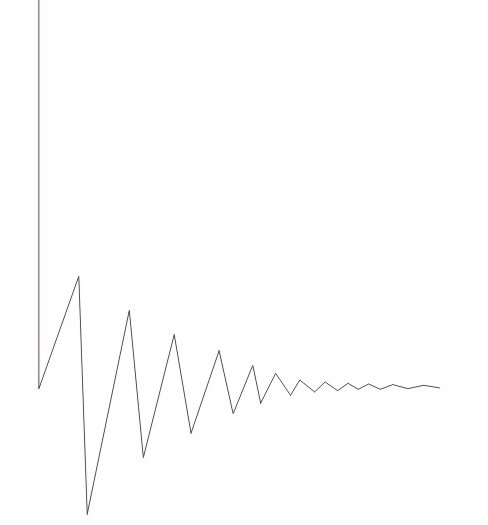
Если я что-либо в чем-либо понимаю, как говаривал Винни-Пух, то вот эта бяка и есть идеальный фрактал рынка. И хотя он вроде сферического коня в вакууме, тем не менее, его можно встретить на любом таймфрейме любого рынка. А вот если бы у распределения рыночных цен не было бы пресловутых «толстых хвостов», то получилось бы примерно вот так:
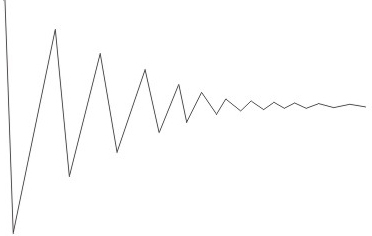
грубоватое изображение «скольугодноузкого треугольника» нормального распределения, но я думаю, вы поняли, что я хотел показать.
Если бы рынок был бы «идеально случаен», но при этом последователен, то он бы всегда ходил конем, а все кризисы были бы L-образные – и было бы скучно. Хорошо, что он не такой:
Мандельбро(т) в своей книге упоминал, что когда они вводили в простенький генератор типа V или L один маааленький элемент случайности – получались очень хитрые кривые. А на рынке то и вовсе, сам генератор/фрактал состоит из случайно расположенных величин случайного размера – ЖУТЬ. Ничего удивительного, что на получающихся кривых люди видят тренды, головы и плечи, я вот драконов с собаками одно время видел, да мало ли чего еще можно вообразить глядя на фрактальную кривую...
тут, наверное, потребуются пояснения. Фрактал рынка – это набор приращений цены от большего (по модулю) к меньшим. И в таком виде он похож на Lили Г. Но по росту приращения выстраиваются довольно редко. Гораздо чаще они выстраиваются микро-сериями по два-три близких размеров, реже в совершенно случайном порядке. Таким, образом случайность размера приращения множится на случайность ее месторасположения.
При всем при этом, самое большое приращение во фрактале определяет его форму при любых положениях остальных движений, именно потому, что оно очень большое, но очень редкое. Как ни крути, а хвост фрактала не может оказаться выше, чем его начало (импульс-длительный откат). А если еще учесть, что большие (но не экстремальные движения) встречаются чаще, но норовят уложиться в мини-серию из 2-3, то теория Эллиота в ее оригинальном варианте 1-5-A-C – описывает наиболее часто встречающуюся (но не единственную) форму фрактала на рынке. Фрактальность же, подразумевает самоподобие целого и его частей, поэтому 1-2 подобно 1-С и в целом все-равно напоминает L (ну или Г если кому так больше нравится).
P.S. После прочтения Мандельбро(т)’а откровением было то, что фрактальную кривую можно построить, используя некую рекурсивную формулу, но ни по какой формуле невозможно определить координаты конкретной точки на этой кривой. Графически на уже построенной кривой – можно, а посчитать – ну никак :(.
С теорией Эллиота видимо та же песня, на графике всегда найдется импуьс и откат (то есть графический способ), но определить, когда начнется новый фрактал, каким в действительности он будет, и в какой части самоподобного фрактала ты сейчас находишься – ну крайне затруднительно в 80% случаев (по Парето). ;)
Ну так вот, пусть не было ничего и вдруг — большой взрыв, ака Большое Ценовое Колебание (вообще даже не суть что это будет, неожиданно охренительные дивиденды, или ужасающая новость)
Фишка в том, что вероятность второго подряд большого движения, но в обратном направлении крайне мала (хотя, конечно и не нулевая). Вероятность движений среднего диапазона – несколько выше, но самая большая вероятность у маленьких движений.
Для компенсации одного мощного движения потребуется множество мелких, направленных в одну, да еще и в противоположную сторону, или несколько средних. При всем при этом, вероятность того, в какую сторону (вверх или вниз) будет направлено каждое из маленьких или средних движений равна почти 1/2 (если не учитывать 5% нулевых приращений цены). Иными словами, одно большое движение, скорее всего, полностью не компенсируется, до появления нового движения того же размера. А в идеальном случае так и вовсе не компенсируется – сумма всех мелких движений будет близка к нулю.
Рынок (да и вообще любой природный процесс) по моему скромному мнению развивается кризисами, а идеальный кризис выглядит примерно так.
Если я что-либо в чем-либо понимаю, как говаривал Винни-Пух, то вот эта бяка и есть идеальный фрактал рынка. И хотя он вроде сферического коня в вакууме, тем не менее, его можно встретить на любом таймфрейме любого рынка. А вот если бы у распределения рыночных цен не было бы пресловутых «толстых хвостов», то получилось бы примерно вот так:
грубоватое изображение «скольугодноузкого треугольника» нормального распределения, но я думаю, вы поняли, что я хотел показать.
Если бы рынок был бы «идеально случаен», но при этом последователен, то он бы всегда ходил конем, а все кризисы были бы L-образные – и было бы скучно. Хорошо, что он не такой:
Мандельбро(т) в своей книге упоминал, что когда они вводили в простенький генератор типа V или L один маааленький элемент случайности – получались очень хитрые кривые. А на рынке то и вовсе, сам генератор/фрактал состоит из случайно расположенных величин случайного размера – ЖУТЬ. Ничего удивительного, что на получающихся кривых люди видят тренды, головы и плечи, я вот драконов с собаками одно время видел, да мало ли чего еще можно вообразить глядя на фрактальную кривую...
тут, наверное, потребуются пояснения. Фрактал рынка – это набор приращений цены от большего (по модулю) к меньшим. И в таком виде он похож на Lили Г. Но по росту приращения выстраиваются довольно редко. Гораздо чаще они выстраиваются микро-сериями по два-три близких размеров, реже в совершенно случайном порядке. Таким, образом случайность размера приращения множится на случайность ее месторасположения.
При всем при этом, самое большое приращение во фрактале определяет его форму при любых положениях остальных движений, именно потому, что оно очень большое, но очень редкое. Как ни крути, а хвост фрактала не может оказаться выше, чем его начало (импульс-длительный откат). А если еще учесть, что большие (но не экстремальные движения) встречаются чаще, но норовят уложиться в мини-серию из 2-3, то теория Эллиота в ее оригинальном варианте 1-5-A-C – описывает наиболее часто встречающуюся (но не единственную) форму фрактала на рынке. Фрактальность же, подразумевает самоподобие целого и его частей, поэтому 1-2 подобно 1-С и в целом все-равно напоминает L (ну или Г если кому так больше нравится).
P.S. После прочтения Мандельбро(т)’а откровением было то, что фрактальную кривую можно построить, используя некую рекурсивную формулу, но ни по какой формуле невозможно определить координаты конкретной точки на этой кривой. Графически на уже построенной кривой – можно, а посчитать – ну никак :(.
С теорией Эллиота видимо та же песня, на графике всегда найдется импуьс и откат (то есть графический способ), но определить, когда начнется новый фрактал, каким в действительности он будет, и в какой части самоподобного фрактала ты сейчас находишься – ну крайне затруднительно в 80% случаев (по Парето). ;)
Да, при последующих техдефолтах скорее всего котировки этой бумаги уже не будут испытывать серьезных колебаний, как на первом и втором. Для примера посмотрите РКК, там было уже 5 техдефолтов суммарно ...
Vic, Похоже Байден фальстартнул)) Зеля укоряет — ничего нет, а ты разрешаешь, трепло! Всё пожгли при недавнем налете на Одессу.
Кстати, а отчего ни один смартлабовский военкор, не выкладывает простыни с экспертизой одного из самых массированных ракетных ударов ВС РФ по энерго инфраструктуре братского, со слов Путина, украинско...
1:22
И вообще. НЛМК такое красивое двойное дно нарисовал.
вамсат вамирекс, какой смысл смотреть этот тенек внебиржевой? Вы посмотрите какие там копеешные обьемы. Это вообще ни о чем не говорит
Сергей Аноним, Император ясно дал понять, что применение таких ракет по нашим тылам будет рассматриваться как прямое участие стран НАТО в конфликте. Т.ч., если вся история не попытка усилить перего...
Александр Ядрихинский, ничего умнее не смог придумать в ответ!
Ну ты давай, тренируй мозг, может, через годик-другой начнут получаться умные мысли.
Один из лучших сайтов!!!
khornickjaadle, Сечин изначально заявил бредовые цифры в которые никто не поверил, со строительством городов на Севере, безумным количеством рабочих и т.д.
Запасы природного газа в ПХГ Европы составляют 112.2 миллиарда кубометров
Данные запасы включают запасы в ЕС, Великобритании и на Украине. Заполненность хранилищ 78% (при общей вместимости — 143 ми...
Автор совершенно нормальный пример приводит… кстати у Эйлера абсолютно точно есть скрипт который эти всплески с затуханием плказывает наглядно… я его для тоса как то переписывал…
4часа и старшие — для ориентации в пространстве :)
Для меня это обычное возвратное движение, FAKE, Shake-out :D
Классический паттерн торговли))
+ пару EMA = и уже готовая стратегия (профитная)
Этот классический паттерн — никто никогда не пытался объяснить с точки зрения математики/теорвер'а (ну во всяком случае мне не попадалось). При том что это проще пареной репы, и давно пора было это сделать.
он и формирует девиации от устойчивого состояния.
Только случайностей не бывает, даже когда на Землю падает метеорит.
«но ни по какой формуле невозможно определить координаты конкретной точки на этой кривой. Графически на уже построенной кривой – можно, а посчитать – ну никак :(»
Если можно построить график по рекурсивной формуле, то можно и определить координаты на двухмерной матрице.
Можно даже разложить готовую матрицу на фракталы методом последовательных фрактальных вычитаний из матрицы.
Таким образом можно увидеть волны Элиота, Вульфа и пр. В чистом виде на любом таймфрейме.
«Этот классический паттерн — никто никогда не пытался объяснить с точки зрения математики/теорвер'а (ну во всяком случае мне не попадалось). При том что это проще пареной репы, и давно пора было это сделать.»
Может быть попробуете прямо сейчас? )))
Я не настолько силен в математике, чтобы спорить с вами или с любым профессором, особенно с тем, кто придумал фрактальную геометрию ;)
UPD: я не просто попробовал, я это уже сделал в трех последних постах, неужели не поняли? :)
«Так что ОЧЕНЬ хотелось бы увидеть эти расчеты. мне бы они пригодились в торговле.»
Это, типа, развести «на слабо»?
Я пока не очень понимаю, как мне самому-то пригодились бы в торговле эти расчеты и какой в них вообще смысл, если мы говорим о нахождении координат точки на ПОСТРОЕННОМ по формуле графике.
Кстати, имеется в виду формула со случайным аргументом на каждой рекурсии что ли?
«я не просто попробовал, я это уже сделал в трех последних постах, неужели не поняли? :)»
Математика — наука точная и в ней «сделал» — значит описал формулой и построил экспериментальную модель по ней.
Все остальное — … ))
Вот мое моделирование от апреля 2011 на 4 года вперед..
Сирневая линия показывает где будут отскоки и коррекции
Вот от июля 2012… если бы не левые котировки, было бы совсем точно.
И вот март 2014, как видите, прогнозировалась чистой воды медвежья 5-тиволновая фигура Элиота идеальной параболической формы. Но кукл из нее сделал прямую линию, хотя и уперся в ту самую линию поддержки. Временные характеристики волны
сжаты в 4 раза!!! Хотя, ее можно разложить в пятиволновку, один хрен..
формула со случайным элементом в генераторе фрактала, на каждой рекурсии — я об этом.
Математика — точная, модель я и построил (чем никто раньше не занимался, да на пальцах, а почему нет?), формула, задающая это распределение случайных величин описана задолго до меня во многих книгах.
Просто я не собираюсь дисер защищать по этой теме — раз. Загромозди я посты математикой — их бы даже читать никто не стал — два.
а прогнозы — они такие прогнозы. Что вы будете делать если евра быстро отскочит до 1,31 а потом прорвет эту линию и пойдет ниже — это будет черный лебедь, да. труднопрогнозируемая хрень -согласен, но, черт возьми, возможная. При этом я гарантирую вам, что если это произойдет — это будет мощное и БЫСТРОЕ движение. И ваша модель до окончания этого движения не будет правильно работать. Как только движение закончится — ваша модель снова станет работоспособной. И по ней можно будет торговать с профитом, и единственная закавыка — не сольется ли депо во время черного лебедя :)
я в мае 2008 расчитал, что евра уйдет ниже паритета, и на падении ее в восьмом умудрился кое-что заработать. Она уйдет обязательно и много ниже (но прошло уже шесть лет) а она все еще не ушла. — если бы я продолжал сидеть в той позе, которую открыл в мае 2008 в святой уверенности что прогноз верный — я сейчас был бы в плюсе, но шесть лет в позе!!! -это не мой таймфрейм ;))
UPD: то что вы говорите «кукл сжал временные характеристики» — косвенно говорит о том, что сейчас моделировать правильный прогноз надо на большем таймфрейме — то есть идет перход фрактальной структуры на более крупный порядок (ИМХО, конечно же)