28 апреля 2015, 16:22
Тест системы на неслучайность
Собственно, опишу критерий, по которому я сделал вывод о пригодности систем на основе EMA для торговли фьючерсами на индекс РТС и пару доллар-рубль. Сами рассуждения никоим образом не привязаны к этим конкретным инструментам, вся концепция не выходит за пределы статистики, то есть ее можно применять для оценки моделей любых случайных процессов и котировок чего угодно.
Для простоты рассмотрим цену на инструмент как случайный процесс с дискретным временем. Например, можно взять среднюю цену того же фьючерса за минуту и считать её ценой фьючерса в эту минуту. От минуты к минуте цена случайным образом изменяется, то в большую, то в меньшую сторону.
Время: 10:20:30, 10:20:31, 10:20:32, 10:20:33, 10:20:34, 10:20:35...
Цена: 1000, 1001, 1002, 1000, 998, 998, 997...
Приращение: 0, 1, 1, -2, -2, 0, -1...
В контексте торговли нам как раз интересна последовательность приращений цены. Можно взять не арифметическую разность соседних значений, а логарифм их отношений, суть от этого не меняется. Ведь в чём заключается процесс торговли: по сути мы берем график, выделяем на нём отрезки времени путём совершения сделок, далее эти выделенные куски вырезаем, те что в шорт переворачиваем и склеиваем их все вместе обратно. Цель процесса — чтобы полученный таким образом новый график рос быстрее, а падал медленнее, чем исходный.
Далее, опять же для простоты, предполагаем, что наша система совершает сделки только в лонг. Для каждого отдельного приращения, в соответствии с правилами системы, известно, открыта в данный момент времени сделка, или нет. Таким образом, торговая система по определенным правилам разбивает общее множество всех случайных ценовых приращений за определенный период на две выборки — те, что «внутри» сделки и участвуют в росте эквити системы, и те, что «снаружи», и не участвуют.
Так вот, мы, как разработчики торговой системы, принципиально хотим, чтобы средние значения у этих двух выборок различались. Иначе просто теряется смысл торговли по этой системе, с тем же успехом можно открывать и закрывать сделки случайным образом.
По счастью, для целей проверки гипотезы о различии средних значений двух выборок давным-давно придуманы статистические тесты. Нам интересен тест Стьюдента, вернее его модификация для двух выборок разного размера с необязанными совпадать дисперсиями, известная также как тест Уэлча. Ссылка на англоязычную Википедию: goo.gl/CTa5Jc.
Внимание, формула:
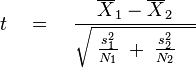
Здесь X1 и X2 с чёрточками — это средние значения, s1^2 и s2^2 — выборочные дисперсии, а N1 и N2 — количество элементов для первой и второй выборок, соответственно. Считаете эти параметры для каждой выборки, получаете конкретное значение t. Уже когда размеры обоих выборок составляют порядка нескольких десятков элементов, распределение значений t очень близко к нормальному с матожиданием 0 и дисперсией 1. Соответственно, чем больше абсолютное значение t для конкретной пары выборок, тем интереснее для нас та система, с помощью которой они были получены. Фактически, это количество «сигм», стандартных отклонений от матожидания нормального распределения для данной системы, показывающее вероятность того, что она ведёт себя на рынке случайным образом.
С увеличением периода тестирования и, соответственно, размеров выборок, у интересной системы критерий t постепенно растёт до интересных значений. Из практики и простого научного здравого смысла, начинаются эти значения где-то в районе шести (сигм). Системы с t меньше шести — скорее всего ни о чём. Те, о которых я писал в предыдущем посте, на EMAшках на минутках, дают порядка 8-9 сигм, и это только за период с середины марта для фьюча SiH5.
Вот так вот как-то так, умеющий читать да прочитает!
Всем профита (по мере сил).
Для простоты рассмотрим цену на инструмент как случайный процесс с дискретным временем. Например, можно взять среднюю цену того же фьючерса за минуту и считать её ценой фьючерса в эту минуту. От минуты к минуте цена случайным образом изменяется, то в большую, то в меньшую сторону.
Время: 10:20:30, 10:20:31, 10:20:32, 10:20:33, 10:20:34, 10:20:35...
Цена: 1000, 1001, 1002, 1000, 998, 998, 997...
Приращение: 0, 1, 1, -2, -2, 0, -1...
В контексте торговли нам как раз интересна последовательность приращений цены. Можно взять не арифметическую разность соседних значений, а логарифм их отношений, суть от этого не меняется. Ведь в чём заключается процесс торговли: по сути мы берем график, выделяем на нём отрезки времени путём совершения сделок, далее эти выделенные куски вырезаем, те что в шорт переворачиваем и склеиваем их все вместе обратно. Цель процесса — чтобы полученный таким образом новый график рос быстрее, а падал медленнее, чем исходный.
Далее, опять же для простоты, предполагаем, что наша система совершает сделки только в лонг. Для каждого отдельного приращения, в соответствии с правилами системы, известно, открыта в данный момент времени сделка, или нет. Таким образом, торговая система по определенным правилам разбивает общее множество всех случайных ценовых приращений за определенный период на две выборки — те, что «внутри» сделки и участвуют в росте эквити системы, и те, что «снаружи», и не участвуют.
Так вот, мы, как разработчики торговой системы, принципиально хотим, чтобы средние значения у этих двух выборок различались. Иначе просто теряется смысл торговли по этой системе, с тем же успехом можно открывать и закрывать сделки случайным образом.
По счастью, для целей проверки гипотезы о различии средних значений двух выборок давным-давно придуманы статистические тесты. Нам интересен тест Стьюдента, вернее его модификация для двух выборок разного размера с необязанными совпадать дисперсиями, известная также как тест Уэлча. Ссылка на англоязычную Википедию: goo.gl/CTa5Jc.
Внимание, формула:
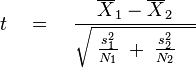
Здесь X1 и X2 с чёрточками — это средние значения, s1^2 и s2^2 — выборочные дисперсии, а N1 и N2 — количество элементов для первой и второй выборок, соответственно. Считаете эти параметры для каждой выборки, получаете конкретное значение t. Уже когда размеры обоих выборок составляют порядка нескольких десятков элементов, распределение значений t очень близко к нормальному с матожиданием 0 и дисперсией 1. Соответственно, чем больше абсолютное значение t для конкретной пары выборок, тем интереснее для нас та система, с помощью которой они были получены. Фактически, это количество «сигм», стандартных отклонений от матожидания нормального распределения для данной системы, показывающее вероятность того, что она ведёт себя на рынке случайным образом.
С увеличением периода тестирования и, соответственно, размеров выборок, у интересной системы критерий t постепенно растёт до интересных значений. Из практики и простого научного здравого смысла, начинаются эти значения где-то в районе шести (сигм). Системы с t меньше шести — скорее всего ни о чём. Те, о которых я писал в предыдущем посте, на EMAшках на минутках, дают порядка 8-9 сигм, и это только за период с середины марта для фьюча SiH5.
Вот так вот как-то так, умеющий читать да прочитает!
Всем профита (по мере сил).










Думаю, что дело обстоит чуть иначе. Они сначала неэффективности создают, затем играют на них, пока «число сигм" не упадёт ниже некоторого значения.
Мы же со стороны это наблюдаем, и если успеваем, то присоединяемся, проведя соответствующие вычисления, как автор.
2. Зачем сравнивать то, что внутри сделки с тем, что снаружи? Вроде, логично сравнивать среднюю сделку с нулем. Мы ж деньги хотим зарабатывать а не b&h обгонять.
1. При тестировании на истории мы имеем дело с реализацией процесса, а среднее по случайной выборке стремится к нормальному независимо от формы распределения в самой популяции, в силу той же ЦПТ. В этом всё и дело, тут не вводится никаких искусственных предположений о нормальном распределении приращений цен, ибо это очевидно не так.
2. Чтобы отличить выигрышную систему от торгующей случайно на длинном тренде. Не знаю как Вы, а я хочу обгонять B&H, причём со страшной силой )) Иначе это не зарабатывание денег, а «шадринг», понравился мне этот термин.
2. Это философский вопрос :) Я хочу денег--стабильно, и, как следствие стабильности, много. Плавная растущая эквити--вот цель, и испиленный с рисками в 100% b&h тут точно не конкурент и не бенчмарк.
1. Да, очевидно, результаты сделок не распределены нормально, поскольку ценовые приращения внутри сделки не являются случайной выборкой. Система может выбирать периоды повышенной волатильности, и дисперсии приращений внутри и вне сделок могут существенно отличаться. Именно по этой причине используется критерий для выборок с неодинаковой дисперсией. Но его значение уже имеет нормальное распределение )
2. Я тоже хочу много денег )) Главное тут понимание оптимального направления в каждый момент времени, а как на этой основе пилить график и с какими объемами и рисками — это уже отдельная тема и свои ноу-хау.
Иными словами, как понять, что надо отключать?
1) Речь о системе, которая переподогнана под конкретный набор исходных данных? Разумеется, для такой системы значение теста будет просто космическим. С другой стороны, вероятность случайно выбрать именно данную конкретную систему из всего множества подобных с таким же числом степеней свободы будет исчезающе малой.
Поэтому:
2) Для переподогнанной системы не будет гарантировать нинасколько. А если мы создаем набор из нескольких тысяч систем и находим среди них такие, которые чисто случайно появляются с вероятностью одна на миллиард, причём не одну а пару десятков, то в них уверенности уже будет побольше.
Комменты не перечитывал, если надо — осилю. )
А если система имеет 3 состояния — лонг, шорт, аут, Вы считаете 3 статистики?
Я понял так, что Вы по тикам считаете секундные бары и на их основе строите системы. И при расчете этих статистик бары тоже секундные или более медленный таймфрейм. И вообще, о какой примерно частоте сделок идет речь при работе на секундных барах?
Я работаю на минутках.
SergeyJu, если система имеет три состояния, то котируется считать лонг и шорт отдельно, как будто у нас две системы — одна лонг и одна шорт. Соответственно считаем 4 средних: лонг, шорт+аут, шорт, лонг+аут, и сравниваем первое со вторым и третье с четвёртым.
Бары я не считаю, для каждой секунды считается одна цена — VWAP (volume-weighted average price). Секундный интервал нужен для того, чтобы набрать нужное для анализа количество исходных точек данных — это порядка неск сот тысяч для одного инструмента. С частотой сделок это связано чуть менее, чем никак, она настраивается через, например, периоды используемых индикаторов, которые по этим секундным средним ценам считаются.
Вообще система сама по себе трендовая, соответственно чем длиннее средняя сделка (выловленный тренд), тем лучше.
Несколько сот тысяч секунд, это два-десять торговых дней. Неужели расчет по секундам дает дополнительный плюс к расчету по минутам. Или для Вас важна скорость реакции?
Я тоже торгую трендследящие системы. И у меня вполне обычно, что группа однородных систем с чуть-чуть разными параметрами входи в рынок (выходит) 10-20 минут.
Например я ещё могу захотеть из любопытства построить модельку для последнего месяца и сравнить с годом, что там у них есть общего а чего нет и т д. Короче, самый универсальный таймфрейм )
Кстати, более устойчивая конструкция, особенно для ликвидных, но не слишком ликвидных активов.
В общем-то я хочу перейти со временем в более быстрый таймфрейм, но не по тем соображениям, что у Вас.