Как потестить систему в Экселе. Пошагово. Часть 3
9.) Посчитаем коэффициенты Шарпа и Сортино. Эти коэффициенты оценивают риски, связанные с волатильностью доходности системы, и соотносят рисковую доходность системы с безрисковой доходностью (например, по облигациям или по банковскому вкладу). Таким образом, коэффициенты Шарпа и Сортино позволяют оценить финансовую целесообразность системы. Ключевое различие между коэффициентами в том, что коэффициент Шарпа не делает различий между колебаниями доходности вверх и колебаниями доходности вниз, то есть резкое увеличение прибыли он оценивает так же негативно, как и резкое увеличение убытков (что может негативно сказаться на оценке классических трендовых систем, рассчитанных на ловлю больших движений и демонстрирующих крайне низкий процент прибыльных сделок). А коэффициент Сортино считает рисковой только ту доходность, которая отличается от безрискойвой доходности по ставке в худшую сторону.
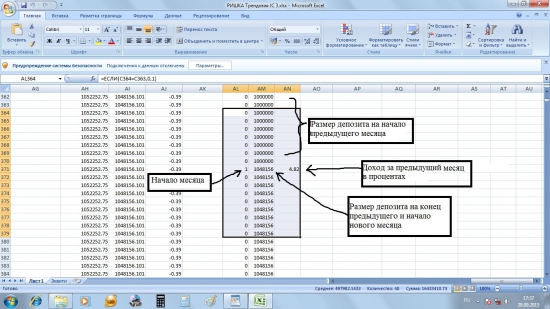
Шарп рассчитывается так: из средней доходности торговой системы за определённый период вычитается средняя доходность по безрисковой ставке и полученный результат делится на стандартное отклонение доходности. В нашем тесте мы рассчитаем доходность системы за каждый месяц. Для рассчёта коэффициента будем использовать среднемесячную доходность. За безрисковую ставку мы возьмём 12% годовых — доходность, которую можно получить по банковскому вкладу и которую легко посчитать по месяцам, просто поделив на 12. Для расчёта доходности по месяцам мы используем 3 столбца: AL, AM и AN. Нам необходимо определить величину депозита на начало каждого месяца и величину депозита на конец каждого месяца. Затем, посчитав разность между вторым и первым и выразив её в процентах, мы и получим искомую доходность. В первом столбце (AL) мы отметим начало каждого месяца. В ячейке AL3 формула:
=ЕСЛИ(C3=C2;0;1)
Она отсылает нас к столбцу C, где указан порядковый номер в году каждого месяца. «Если номер в текущей ячейке столбца С равен номеру в предыдущей ячейке, значит месяц продолжается — в текущуюю ячейку столбца AL ставится 0; в ином случае ставится единица, отмечая начало нового месяца».
В столбце AM мы определим величину депозита на начало и конец каждого месяца. Используем самый простой вариант: размер депозита на начало последуещего месяца одновременно будет являться размером депозита на конец предыдущего. Кроме того мы будем учитывать только закрытые позиции: если на начало месяца остаётся позиция, открытая в прошлом месяце или раньше, её объём на тот момент не будет учитываться как объём депозита. Пишем формулу в ячейку AM4:
=ЕСЛИ(AL4=1;AB4;AM3)
«Если текущая ячейка AL указывает на начало месяца, в текущую ячейку AM заносится текущее значение депозита из столбца AB; в ином случае значение текущей ячейки AM равно предыдущему значению ячейки AM».
Наконец в столбце AN, начиная с ячейки AN4, посчитаем доходность каждого месяца в процентах:
=ЕСЛИ(AL4=1;(AM4-AM3)/AM3*100;"")
«Если текущая ячейка AL указывает на начало месяца, из текущего значения ячейки AM вычитается предыдущее и полученный результат выражается в процентах; в ином случае ячейка остаётся пустой».
Не забываем полученные формулы провести по столбцам.
В столбцах AO, AP, AQ и AR будут размещены отрицательная доходность, а также будут рассчитаны формулы необходимые для получения коэффициента Сортино. Их пока пропустим.
В ячейке AS2 посчитаем среднемесячную доходность (среднее значение диапазона столбца AN):
=СРЗНАЧ(AN2:AN15283)
В ячейке AT2 посчитаем коэффициент Шарпа — из среднемесячной доходности нашей системы вычтем среднемесячную доходность по безрисковой ставке (её мы взяли за единицу) и полученный результат разделим на стандартное отклонение среднемесячной доходности (дипазона столбца AN). Стандартное отклонение мы будем считать по генеральной совокупности (функция СТАНДОТКЛОНП):
=(AS2-1)/СТАНДОТКЛОНП(AN2:AN15283)
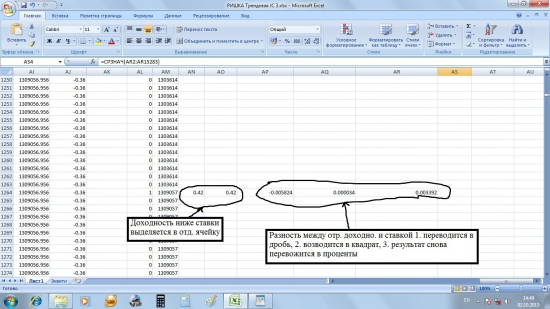
Теперь посчитаем коэффициент Сортино. Для его расчёта нам понадобятся только отрицательные значения доходности по месяцам. Выделим их в отдельный столбец AO с помощью формулы в ячейке AO4:
=ЕСЛИ(AN4<1;AN4; ЕСЛИ(AN4="";"";0))
(Напоминаю, что 1 — это среднемесячная безрисковая доходность).
Формула читается так: «Если значение доходности ниже доходности, полученной по безрисковой ставке, это значение указывается в столбце AO; если значение доходности не указано, то ячейка в столбце AO остаётся пустой; в ином случае — если значение доходности указано и оно выше, либо равняется доходности по безрисковой ставке, в столбце AO пишется 0».
Обратите внимание, что положительная доходность из расчётов не исключается — просто ей присваивается нулевое значение.
Проводим формулу через столбец.
Самый простой способ получить очень грубый аналог коэффициента Сортино — посчитать коэффициент Шарпа со стандартным отклонением только по отрицательной доходности. Но для корректного расчёта нужно произвести нижеописанные действия.
Числитель коэффициента Сортино соответствует числителю коэффициента Шарпа. А вот числитель отличается тем, что в его основе не отклонение текущего значения доходности от средней доходности, а отклонение отрицательной доходности от доходности по безрисковой ставке. Мы посчитаем знаменатель в несколько этапов: 1. В столбце AP посчитаем разность между отрицательной доходностью и ставкой и переведём результат из процентов в десятичную дробь (разделим на 100). В ячейке AP4 пишем формулу:
=ЕСЛИ(И(AO4<1;AO4<>0);(AO4-1)/100; ЕСЛИ(AN4="";"";0))
Отклонение положительной доходности от ставки рассчитывать не нужно, но ей должно быть присвоено нулевое значение.
Проводим формулу через столбец.
2. В столбце AQ посчитаем квадрат полученной разности:
=ЕСЛИ(AP4="";"";AP4^2)
3. Наконец в столбце AR переведём полученный результат снова в проценты:
=ЕСЛИ(AQ4="";"";AQ4*100)
В отдельных ячейках столбца AS рассчитаем оставшиеся значения.
В ячейку AS4 пишем формулу:
=СРЗНАЧ(AP2:AP15283)
Получаем среднее значение нашего квадрата разности.
В ячейку AS6 переведём среднее значение в дробь:
=AS4/100
В AS8 вычислим корень из дроби:
=КОРЕНЬ(AS6)
В ячейке AS10 переведём результат в проценты:
=AS8*100
В ячейке AU2 посчитаем коэффициент Сортино (числитель будет тот же, что и у коэффициента Шарпа):
=(AS2-1)/AS10
Дополнительно в ячейке AU4 посчитаем огрублённый вариант Сортино (в знаменателе — стандартное отклонение по ген. совокупности столбца AO).
Вот что у нас получается в итоге:
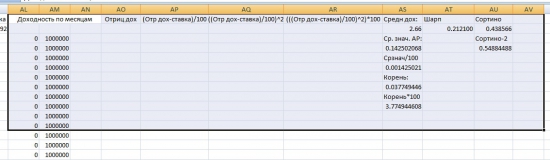
Теперь, когда все основные параметры для оценки системы заданы, потестируем систему на новейших данных. (С января 2012 до конца сентября 2015).
Удалим данные из первых столбцов, где указаны параметры котировок и вместо них экспортируем данные за указанный период. Проделываем ту же процедуру, что и в прошлый раз. Не забываем так же разделить столбец «DATA» на три: Год, Месяц, День. Вот что получаем в итоге:
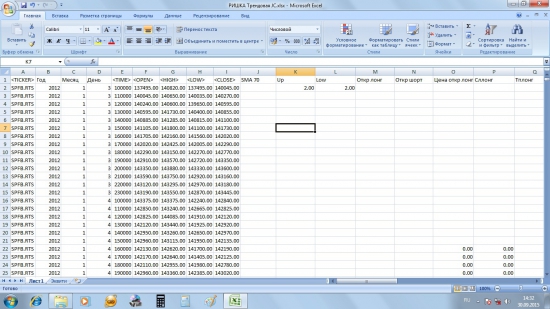
Поскольку мы получили меньше данных, чем при тесте первого ценового ряда, нам необходимо удалить те строки в конце таблицы, продолжает производиться расчёт параметров системы, иначе наши коэффициенты будут учитывать значения этих пустых ячеек. Выделяем лишние строки и нажимаем «Удалить» (не «Очистить содержимое», а именно «Удалить», чтобы нам не пришлось вручную вносить изменения в формулы, которые считают значения диапазонов).
Теперь мы можем оценить нашу систему на свежих данных. Вот что имеем:

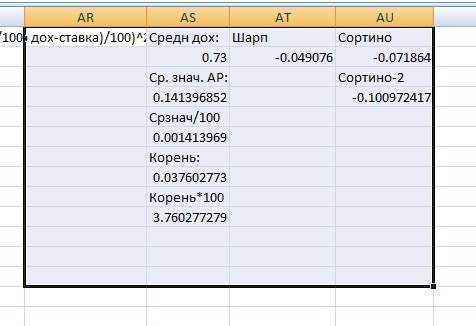
Низкий профит-фактор. Высокая МаксПросадка. Коэффициенты Шарпа и Сортино показыват отрицательные значения.
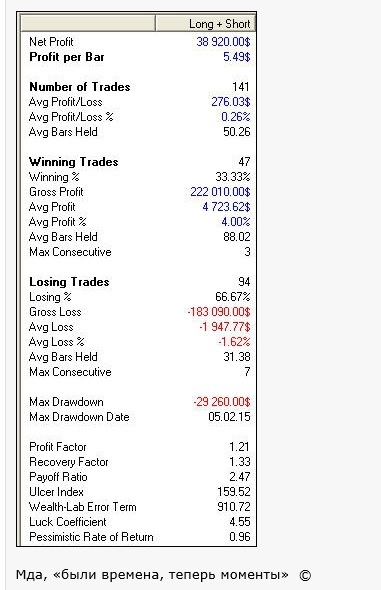
Собственный тест на Велс-Лабе провёл tim (см. комментарии к предыдущей части). Вот его результаты:
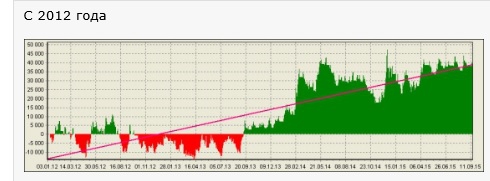
Опять видим заметные расхождения. Также обратим внимание на различия в проценте прибыльных сделок и различия профит-фактора:

Для большей наглядности я построил в Экселе график того же типа, что и в Велс-Лабе, то есть график, показывающий накопленную прибыль/убыток. Через столбец AV я протянул следующую формулу — в ячейке AV3:
=AV2+(AB3-AB2)
«К предыдущему значению столбца прибавлется разница между текущим и предыдущим размером депозита».
Благодаря этому графику становится видно, насколько велика разница между результатом, полученным в Экселе и результатом, полученным в Велс-Лабе:
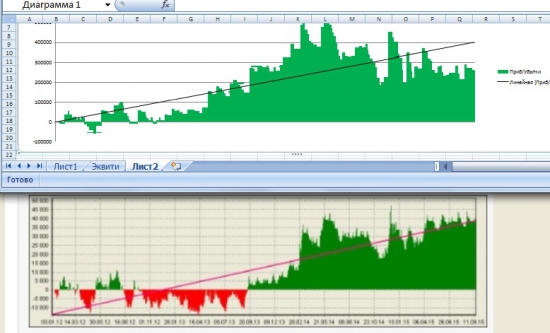
По всей видимости, tim просто использовал несколько иные параметры системы, поскольку описанные ниже небольшие исследования свидетельствуют, что в Экселе ошибок нет.
Я снова провёл проверочный тест в Метастоке и получил результат в целом аналогичный результату Экселя:
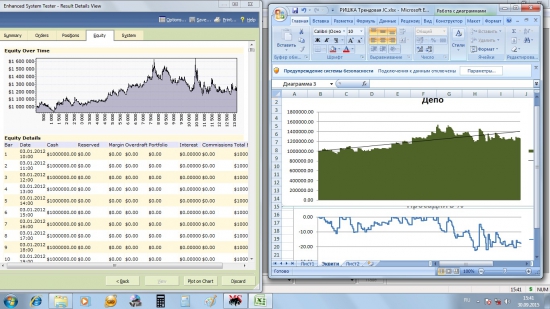
Но ещё более существенным фактом является различие в количестве сделок: в тесте tim была совершена 141 сделка, в моём тесте в Экселе -154 сделки, в Метастоке — 160. То есть различие между экселем и Велс-Лабом — почти 10%, что вряд ли можно считать статистической погрешностью. Ошибок в моей таблице в Эксель нет. Все условия заданы чётко и Эксель их исправно выполняет. Поэтому я решил провести небольшое исследование — сравнить Боллинджер, полученный в Экселе с Боллинджером, взятым из Квика. Я взял ближайший контрак Ри (RiZ5), нанёс на него стандартный Боллинджер (Simple-20-2-Close), после чего экспортировал два полученных массива данных в Эксель. Параллельно квиковскому Боллинджеру я рассчитал индикатор вручную как два стандартных отклонения от 20-ти периодной скользящей средней (как и в прошлый раз я использовал функция СТАНДОТКЛОН). Затем при помощи функции КОРРЕЛ я посчитал корреляцию между двумя Боллинджерами и по отдельности корреляции между верхними полосами и нижними. Вот что получилось:
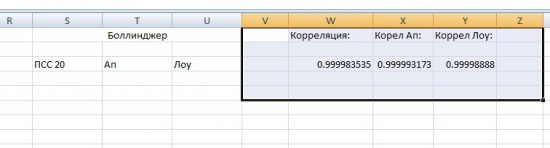
Как видим, корреляция стремится к 100 процентам, однако полного сходства не наблюдается. Для наглядности я взял наугад один фрагмент двух Боллинджеров. Слева три столбца — Боллинджер из Квика, справа — посчитанный вручную:
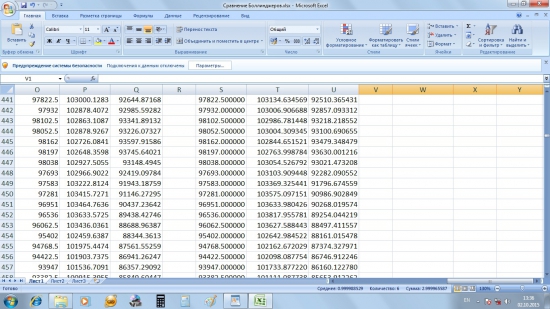
Расхождения несущественны, но они есть. Я полез в мануал Квика, посмотреть, по какой формуле там рассчитывается Боллинджер. Оказалось, что стандартное отклонение там рассчитывается за N периодов, то есть по генеральной совокупности, а не по выборке. Это значит, что для рассчёта Боллинджера в Экселе лучше использовать функцию СТАНДОТКЛОНП, а не СТАНДОТКЛОН. Я заново рассчитал Боллинджер, на этот раз по функции СТАНДОТКЛОНП и вот что получил:
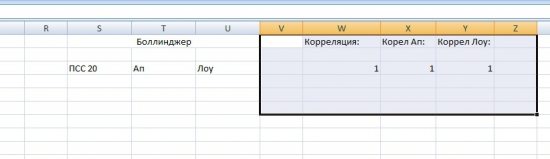
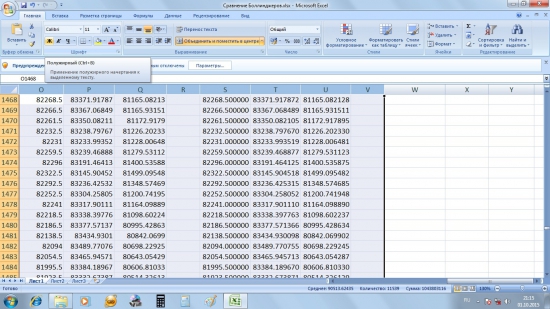
Стопроцентная корреляция.
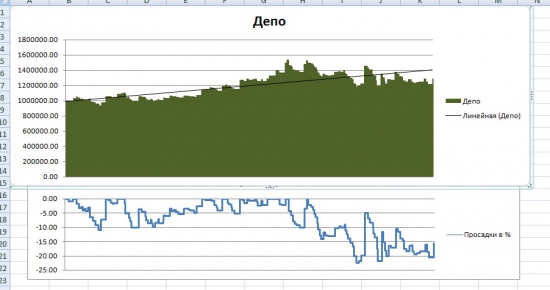
Также я поменял формулу Боллинджера в рассчётах при тестировании системы. Но, как видим, на итоговый результат это не повлияло. Сверху график эквити, полученный при формуле Боллинджера, рассчитанной по СТАНДОТКЛОН, снизу — по СТАНДОТКЛОНП:
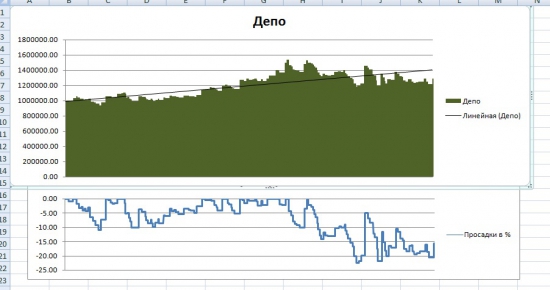
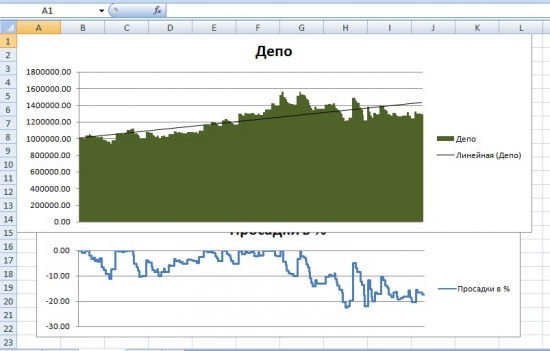
Таким образом, можно сделать вывод, что в Экселе ошибки нет: Эксель показывает ровно тот результат, который может быть получен при торговле на российской бирже через Квик.
В общем, всем удачи в нашей нелёгкой игре:)










Всего 3 поста и уже диссертация!