27 ноября 2018, 12:46
Решил задачу без интернета! Кайф!))
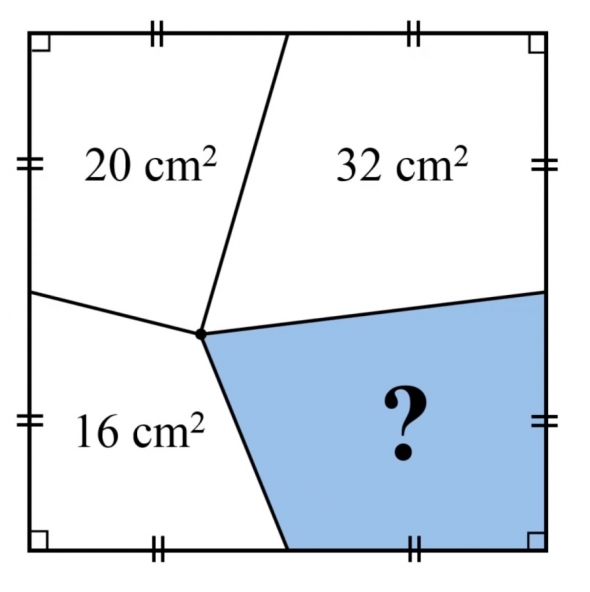
Попробуйте решить эту задачу без использования интернета:
Загрузите мозг. Не ищите готовое решение в интернете. Если сможете решить, то гарантированно получите выброс эндорфинов в кровь и, как следствие, испытаете удовольствие. Это произойдет благодаря древней подпрограмме в нашем мозге, награждающую нас за решение сложной задачи. Благодаря ей человечество сейчас занимается трейдингом и летает в космос, а не сидит на пальме с голой жопой.
Удачи!))

Загрузите мозг. Не ищите готовое решение в интернете. Если сможете решить, то гарантированно получите выброс эндорфинов в кровь и, как следствие, испытаете удовольствие. Это произойдет благодаря древней подпрограмме в нашем мозге, награждающую нас за решение сложной задачи. Благодаря ей человечество сейчас занимается трейдингом и летает в космос, а не сидит на пальме с голой жопой.
Удачи!))










Он задачки подкидывает!!!
из шорта уже вышел… и пока не вижу тут новую позу… время еще не пришло)
отскочит — пошорчу… а пока лучше посижу на заборе)
А ваш не удобен для профитной торговли!!!
Есть мнение, что суммы площадей по диагонали равны.
20 + x = 32 +16
Соединим «центр» с вершинами квадрата (разобьем четырехугольники на пару трегольников). Посчитаем площади четырехугольников на основе формулы площади треугольника (половина произведения основания на высоту).
Обозначим высоты треугольников (перпендикуляры на стороны квадрата) как a,b,c,d. Пусть половинка стороны квадрата — х.
Тогда для одной пары диагональных прямоугольников
16=x*a/2 + x*d/2
32=x*b/2 + x*c/2
48=x*(a+b+c+d)/2
Упрощаем, заметив, что a+c = b+d = 2*x — сторона квадрата, можно и сторону квадрата вычислить (интересная, кстати).
48=x*4*x/2=2*x*x — площадь пары диагональных четырехугольников.
(Тут еще вариант решения напрашивается, надо отметить центр квадрата — вряд ли будет проще).
Инвариант, действительно, не зависит от положения «центральной» точки, это же имеем и для другой диагональной пары.
Как следствие — подтверждается выдвинутая гипотеза о равенстве сумм площадей диагональных пар четырехугольников, хотя это и лишнее.
48=20 + ?
? = 28
P.S. Не тянет на 8 класс. Может, на 5-6?
Ой, а я что то сложным путем пошел — через уравнение по высотам треугольников из малого квадрата. ))) Вывел стороны квадрата, а дальше дело техники ))) Я там в арифметике только ошибся, так что 96-68 = 28, исправить забыл
не смог решить
завтра вернусь
понимаю как составить систему уравнений, но решать ее лень
Если изначально линии вернуть строго по центру, то получится квадрат разбит на равные четрые доли. Сместив точку с осями, задача любезно предоставила нам к известности площадь трех долей. Чтобы найти размер оставшейся, помним изначально все было равно друг другу. Соответственно если при смещении вышло так, что площадь первой доли стала равняться 20 см 2, а вторая при этом 32 см, то легко можно подсчитать оставшиеся соотношениями: нижняя доля левая доля равна 16 см2, на 4 см2 меньше, чем вернхяя левая. Соответсвенно нижняя правая тоже будет на 4 см2 меньше. 32-4 =28.
Итого 28+16+32+20=96/4 изначально доли были по 24см2