Идеальная ставка. В азартных играх на смену удаче приходит научный подход. История обмена идеями между наукой и индустрией азартных игр. Адам Кучарски

Идеальная ставка. Адам Кучарски. Adam Kucharski. THE PERFECT BET 
Электронная книга t.me/kudaidem/1867

Кто хоть раз в жизни не слышал об «идеальной ставке»?

Любители азартных игр веками ищут волшебную формулу, с помощью которой смогут обыграть казино или букмекера, бросив вызов самой Фортуне. С недавних пор к этим поискам присоединились ученые.
Исследование принципов и механизмов азартных игр  позволило некоторым из них совершить открытия в самых разных областях науки, от статистики до теории хаоса и конструирования искусственного интеллекта.

Кое-кто из них еще и выиграл кругленькую сумму.

Азартные игры – настоящая фабрика невероятных идей, поражающих своей оригинальностью и дерзостью.

Математик и журналист Адам Кучарски рассказывает в книге «Идеальная ставка» увлекательную историю обмена идеями между наукой и индустрией азартных игр.

(Предисловие).

В 2009 году в газеты попала история Эллиота Шота – финансового трейдера, выигравшего на скачках более 20 миллионов фунтов.

Шот, говорилось в статье, использовал простую стратегию: всегда ставил против фаворита. Поскольку лошадь с наибольшими шансами на победу приходит первой далеко не всегда, такой метод способен принести большие деньги.

Благодаря своей системе Шоту удалось дважды сорвать немалый куш – полтора миллиона фунтов во время скачек на Челтнемском фестивале и три миллиона на Королевских скачках в Аскоте.

В этой истории была лишь одна маленькая загвоздка – все от начала и до конца оказалось враньем.

Ни в Аскоте, ни в Челтнеме, Шот ничего не выиграл.

Убедив инвесторов вложить в его систему ставок десятки тысяч фунтов, бо́льшую часть денег он потратил на клубы и развлечения. В конце концов у инвесторов возникли вопросы, и Шота арестовали.

В 2013 году он был признан виновным в мошенничестве по девяти статьям и приговорен к пяти годам лишения свободы.

Может показаться удивительным, как Шоту удалось обдурить столько народу, но легенда об идеальной ставке и вправду ужасно привлекательна. 

Человечество с момента зарождения азартных игр пытается обмануть систему.

Однако поиск идеальной ставки занимает умы не одних картежников и любителей рулетки. Азартные игры постепенно заставили все человечество переосмыслить само понятие удачи.

Большинство систем ставок отличались завлекательными названиями и крайне низким коэффициентом результативности. Одна из таких систем именовалась мартингейл.

 Ставки следовало удваивать после каждого проигрыша. Когда в конце концов игроку выпадал нужный цвет, он мог вернуть все, что проиграл ранее, а заодно получить прибыль в размере первоначальной ставки. На первый взгляд система казалась безупречной, однако имела большой недостаток: иногда ставки приходилось повышать так, что они становились неподъемными не только для игрока, но и для казино.

Следуя системе мартингейла, вы могли получить небольшую прибыль на начальном этапе, но в долгосрочной перспективе возникала проблема платежеспособности, мешавшая осуществлению стратегии.

Несмотря на популярность мартингейла, выгодным предприятием его применение назвать было нельзя – слишком велики были затраты.

«Мартингейл неуловим, как сама душа», – утверждал Александр Дюма.

Паскаль и Ферма вывели для игры «ожидаемое значение» – параметр, измерявший вероятность выигрыша при множестве партий. 

Любители азартных игр могут по праву назвать себя крестными отцами теории вероятности.

Бернулли осмыслил проблему с позиции «ожидаемой целесообразности». Он предположил, что одно и то же количество денег имеет бо́льшую или меньшую ценность в зависимости от того, сколько денег имеется у человека. Для бедного человека одна монета гораздо ценнее, чем для богатого. 

Математики оценивают деньги соразмерно их количеству, здравомыслящие люди – соразмерно возможности их использования.

Концепция целесообразности лежит в основе всей индустрии страхования. Большинство людей предпочитают вносить регулярные установленные взносы, чем не платить ничего, рискуя однажды получить огромный счет, даже если платить понемногу выйдет дороже.

Купите вы страховку или откажетесь от нее, зависит от целесообразности.

Люди не склонны страховать то, что в случае утраты будет легко заменить.

Рассмотрим, как азартные игры оказывали влияние на разные области науки – от теории игр и статистики до теории хаоса и технологий по разработке искусственного интеллекта.

Азарт открывает для нас окно в мир возможностей. Игры учат, как найти равновесие между риском и ожидаемым вознаграждением и объясняют, почему в разных обстоятельствах мы придаем определенным вещам разное значение.

Они помогают понять, как наш мозг принимает решения и как мы можем управлять своей удачей.

Объединяя в себе математику, психологию, экономику и физику, азартные игры представляют собой настоящий заповедник для исследователей, которых интересуют случайные или кажущиеся таковыми события.

Изучение связей между наукой и игрой приносит пользу не только ученым. Игроки все активнее используют научные идеи для разработки успешных стратегий. Часто теория совершает круг: алгоритм, рожденный научным интересом к азартным играм, возвращается к своему источнику и становится на службу обычным людям, стремящимся сорвать большой куш в казино.

Физик Фейнман познакомился в Лас-Вегасе с профессиональным игроком Ником по прозвищу Ник Грек. 

Ник открыл Фейнману настоящий секрет своего мастерства.

«Я ставлю на суеверных людей, которые сидят за столом и верят в счастливые числа».

Ник играл против других наивных игроков.

Он понимал суть игры и людскую психологию.

Ник научился предугадывать, когда шансы будут в его пользу.

Главный фокус тут был не в самих расчетах, а в том, как с их помощью создать эффективную стратегию.

Игроки придумывают все новые и новые способы обыграть казино и букмекеров – от предсказания результатов спортивных матчей при помощи статистического анализа до разработки искусственного интеллекта, способного играть в покер лучше человека. 

На протяжении веков азартные игры вдохновляли ученых открывать для себя новые горизонты и расширяли наши познания о случайности и механизме принятия решений.

Методики, применяемые в азартных играх, вышли за пределы казино, они используются в самых разных областях нашей жизни – от технических наук до финансовой индустрии. Раскрыв внутреннюю механику современных игровых стратегий – беттинга, – мы сможем понять, как различные научные концепции продолжают менять наше представление об удаче.

Азартные игры – это настоящая фабрика невероятных идей, простых и изощренных, дерзких и абсурдных.

По всему миру игроки проверяют на прочность пределы предсказуемости и границы между порядком и хаосом. Одни умело пользуются нюансами механизма принятия решений и соревновательного инстинкта. Другие изучают странности человеческого поведения и саму природу мышления. Анализируя успешные стратегии беттинга, мы можем узнать, как азартные игры влияют на наше понимание удачи и как удачей управлять.

Часть 1.Три степени незнания.

Существует два способа понять принцип действия рулетки, и Анри Пуанкаре интересовали оба.

В начале ХХ века внимание Пуанкаре привлекало все, что было связано с математикой.

Он был последним подлинным «универсалом» в своей дисциплине.

Впоследствии ни одному из его коллег не удалось отметиться во всех областях математики и в каждой совершить интересные открытия и установить важные закономерности, как это сделал Пуанкаре.

Пуанкаре полагал, что явления, подобные рулетке, кажутся непредсказуемыми потому, что мы не знаем их причины.

Он предложил классифицировать проблемы по степени нашего незнания.

Если мы точно знаем первоначальное состояние объекта – например, его положение в пространстве и скорость – и как на него распространяется действие физических законов, то мы имеем дело с обычной задачкой из учебника физики.

Пуанкаре назвал это первой степенью незнания: у нас есть вся необходимая информация и нужно лишь произвести несложные вычисления.

Вторая степень незнания – когда мы знаем, как на объект воздействуют физические законы, но не знаем первоначального положения объекта или не можем точно его измерить. 

В этом случае мы должны либо усовершенствовать систему измерения, либо ограничить область прогнозирования того, что случится с нашим объектом в ближайшем будущем. И наконец, третья, наиболее обширная степень незнания – когда мы не знаем ни первоначального состояния объекта, ни воздействия на него законов физики.

Мы также сталкиваемся с третьей степенью незнания, если эти законы слишком сложны, чтобы мы описали их действие.

Допустим, мы уронили банку краски в бассейн с водой.

Мы можем легко спрогнозировать реакцию купающихся, но прогнозировать поведение молекул краски и воды будет намного труднее.

 Траектория шарика на рулетки зависит от множества факторов, которые мы не можем отследить, наблюдая за вращающимся колесом.

Так же как с молекулами воды, мы не можем делать прогнозы о конкретном вращении рулетки, если не понимаем общие закономерности, влияющие на траекторию движения шарика.

Но, нам не обязательно знать, что именно заставило конкретный шарик остановиться здесь.

Мы можем просто пронаблюдать множество вращений и сделать выводы.

Если вращение колеса есть дело случая, то каждый последующий спин не связан с предыдущим. Частота выпадений черного не делает более вероятным выпадение красного.

Однажды шарик «посетил» черное 26 раз подряд! 

Но в тот вечер все игроки верили, что вот-вот выпадет красное. С тех пор эта психологическая ловушка известна как «ошибка игрока» или «ложный вывод Монте-Карло».

Фокус состоит не в том, чтобы найти рулетку, выгодную для ставок.

Даже если, отследив огромное количество спинов, мы установим, что одно из 38 чисел выпадает чаще остальных, этого будет еще не достаточно для получения выгоды.

Число должно появляться не меньше чем один раз за 36 спинов, в противном случае мы все равно проиграем казино.

Находясь на самом глубоком уровне незнания и не понимая причин отдельных явлений, единственное, что мы можем сделать, – осуществить наблюдение за множеством явлений и понять, существует ли между ними закономерность, она же паттерн.

Этот статистический подход хорошо работает с дефектной рулеткой. Не имея знаний о ее физических особенностях, мы тем не менее можем прогнозировать ее поведение.

Проблема, известная как «чувствительная зависимость от начальных условий», заключается в том, что, даже если мы соберем детальную информацию о некоем явлении – будь то вращение рулетки или движение тропического шторма, – малейшее упущение обернется слишком серьезными последствиями.

«Может ли взмах крыльев бабочки в Бразилии запустить торнадо в Техасе?» 

Исследования математика Лоренца, из которых впоследствии выросла теория хаоса, фокусировались главным образом на прогнозировании.

Лоренцем двигало стремление научиться более точно предсказывать погоду и заглядывать в будущее.

Пуанкаре интересовало нечто противоположное: как много времени требуется для того, чтобы процесс стал непредсказуемым? И можно ли считать таковым движение шарика в рулетке?

Рулетка вдохновила Пуанкаре, однако свой прорыв в науке он осуществил, изучая движение значительно более крупных объектов.

В XIX веке астрономы создали карту астероидов, проходящих через созвездия зодиака. Они определили, что астероиды распределяются по звездному небу достаточно равномерно. Пуанкаре хотел понять почему.

Как заметил Пуанкаре, «звездное небо можно представить в виде гигантской рулетки, на которую Создатель бросил множество шариков».

Чтобы понять принцип движения астероидов, Пуанкаре решил сравнить общее расстояние, которое проходит гипотетический объект, с числом его вращений вокруг центра своей орбиты.

Представьте, что вы разворачиваете очень длинный рулон очень гладкой бумаги.

Разложив бумагу на полу, вы запускаете по ней множество шариков.

Шарик, запущенный быстрее, укатится дальше.

Вы фиксируете положение шариков на бумаге, делая надрезы на краю листа бумаги напротив каждого шарика. Затем вы убираете шарики и скручиваете рулон.

Теперь, если вы посмотрите на край рулона, каждый надрез сможет оказаться в любой точке окружности. Это происходит потому, что длина листа и, следовательно, расстояние, которое проходят шарики, намного больше диаметра рулона. Даже небольшая разница в дистанциях, пройденных шариками, значительно отразится на расположении надрезов на окружности.

Если вы скрутите рулон достаточно туго, чувствительная зависимость от начальных условий приведет к равномерному размещению мест надрезов.

Пуанкаре доказал, что, то же самое происходит с орбитами астероидов. С течением времени они равномерно распределяются по поясу зодиака.

Для Пуанкаре и рулетка, и пояс зодиака подтверждали один и тот же принцип.

Ученый предположил, что после большого количества вращений место остановки шарика в рулетке тоже может быть абсолютно случайным.

Он отметил, что определенные варианты ставок попадают в пределы случайности чаще, чем другие. Поскольку ячейки рулетки покрашены попеременно в черный и красный цвета, прогнозирование выпадения того или иного цвета предполагает точный расчет того места, где остановится шарик. Это чрезвычайно трудно даже после одного или двух спинов. Другие виды ставок, например на то, в какой части рулетки остановится шарик, меньше зависят от начальных условий. Здесь потребуется множество спинов, прежде чем результат станет практически случайным.

К счастью для игроков, шарик в рулетке крутится недолго. И в результате игроки могут (в теории) избежать второй степени незнания Пуанкаре путем измерения начального пути шарика. Нужно лишь понять, какие параметры взять для вычислений.

Победа над надежной, хорошо сбалансированной рулеткой – это вопрос физики.

Крутящийся шарик рулетки как планета, которая величественно движется по точной и предсказуемой траектории.

К несчастью для игроков, траектория шарика является, как принято говорить в математике, «нелинейной»: исходные данные (скорость шарика) не прямо пропорциональны выходным данным (месту, где шарик остановится).

Другими словами, это третья степенью незнания.

Один из ученых-эвдемонистов, Томас Басс, запечатлел похождения своей группы  в книге «Эвдемонический пирог».

Хорошенько все просчитав, участники группы спрятали компьютер в ботинке и с его помощью смогли предсказать движение шарика в нескольких казино.

Однако Басс умолчал о самом важном – об уравнении, лежавшем в основе метода эвдемонистов.

В наши дни, другие ученые Смолл и Цэ попытались воспроизвести стратегию эвдемонистов. Они начали с разделения траектории шарика на три фазы.

(рис. 2)

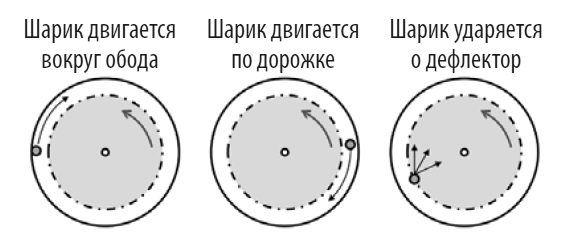
Когда крупье запускает колесо рулетки, шарик сначала двигается вокруг его верхнего обода, в то время как центральная часть рулетки крутится в противоположном направлении. В это время на шарик воздействуют две конкурирующие силы: центростремительная сила удерживает его на ободе, а сила притяжения тянет вниз, к центру колеса.

Во время вращения шарика сила трения замедляет его движение.

Импульс шарика уменьшается.

Шарик переходит во вторую фазу – он сходит с ободка и беспрепятственно движется по дорожке между ободком и дефлекторами. Шарик постепенно смещается к центру колеса до тех пор, пока не столкнется с одним из расположенных на окружности дефлекторов.

До этой точки траекторию шарика может просчитать даже школьник. Но как только он ударяется о дефлектор, его траектория рассеивается, и теоретически он может остановиться в одной из нескольких ячеек.

Для игроков это означает, что шарик покидает мир уютной предсказуемости и погружается в подлинный хаос.

С неопределенностью Смолл и Цэ могли справиться при помощи статистических измерений. 

Смолл не сомневался: стратегия эвдемонистов работает, и наука может победить рулетку.

Вырисовывалось несколько закономерностей.

Шарик останавливался в прогнозируемой ячейке намного чаще, чем если бы его движение было хаотично.

Даже прогнозы, сделанные с помощью секундомера, повышают шансы выигрыша на 18 %.

Смолл начал получать отзывы игроков, использовавших его метод в настоящих казино.

Один парень создал “кликер” – машинки, которую он смастерил из компьютерной мыши и закрепил на большом пальце ноги.

Но, ученый Фармер доказывал, что шарик замедляет не трение, а аэродинамическое сопротивление.

Во время своих вылазок в казино эвдемонисты должны были вычислить три параметра: аэродинамическое сопротивление, скорость шарика в момент его выпадения из обода колеса и скорость, с которой замедлялось колесо.

Предполагалось, что эффект от уменьшения сопротивления приблизительно такой же, как от возрастания скорости.

Крайне важно знать и в каком состоянии находится стол.

Здесь свою роль играет даже погода.

В Санта-Крузе эвдемонисты, которые делали расчеты в солнечную погоду, обнаружили: стоило опуститься туману, и шарик начинал уходить с дорожки на полкруга раньше, чем говорил прогноз.

Хотя теоретически преимущество эвдемонистов перед казино составляло 20 %, из-за технических неполадок оно так и не вылилось в крупный выигрыш.

Со временем компьютеры совершенствовались, и некоторым игрокам все же удавалось использовать их в казино, игроки засекали время вращения рулетки при помощи мобильных телефонов.

Хотя группу и обвинили в мошенничестве с целью получения денег обманным путем, в действительности они не вмешивались в игру.

Никто из них не воздействовал на шарик и не манипулировал фишками.

Спустя девять месяцев после ареста игроков полиция закрыла дело и вернула троице выигрыш в 1,3 миллиона фунтов.

Эволюция успешных рулеточных стратегий наглядно демонстрирует, как последние сто лет развивалась наука об удаче.

Ранние способы обыграть рулетку сводились к тому, чтобы избежать третьей степени незнания – непонимания физических процессов.

Поздние попытки пытались преодолеть второй уровень незнания и предугадать поведение рулетки путем точного измерения исходного состояния шарика и колеса.

Для Пуанкаре рулетка была способом проиллюстрировать свою мысль о том, что простые физические процессы могут претерпевать изменения и производить впечатление непредсказуемых. Эта идея легла в основу теории хаоса, ставшей в 1970-х новой академической дисциплиной.

(2. Счастливый билет). Лотерейные синдикаты.

Как правильно распределять химикаты при обработке растений на экспериментальном участке земли?

Допустим, мы хотим провести тестирование четырех химикатов на шестнадцати пробных участках, расположенных сеткой четыре на четыре.

Как мы можем распылять препараты на территории без риска, что все они попадут в одно и то же место? В исследовании «Организация экспериментов» Фишер предложил систему распыления четырех препаратов, при которой они появляются в каждом ряду и каждой колонке только один раз.

Если экспериментальное поле имеет плодородную почву на одном участке и скудную – на другом, то все химикаты попадут и на тот и на другой тип земли. Оказалось, предложенный Фишером паттерн уже имел широкое распространение в другой области – в классической архитектуре, где был известен как «латинский квадрат».

-

Необходимость создать нечто случайное и сбалансированное одновременно возникает во многих областях производства, включая медицину и архитектуру. Присутствует она и в лотерее.

Лотереи предназначены для того, чтобы забирать у людей деньги.

Они возникли в качестве мягкой формы налогообложения и часто применялись для поддержки крупных строительных объектов.

Возведение Великой Китайской стены было оплачено из доходов от лотереи, организованной династией Хань.

Доходы от лотереи, проведенной в 1753 году, пошли на финансирование Британского музея. Многие университеты Лиги плюща были построены на деньги, вырученные от лотерей.

Сегодня лотереи выглядят по-разному. Наиболее прибыльной частью индустрии в наши дни стали скретч-карты, но, здесь нужна «контролируемая случайность».

Выигрышные скретч-карты встречаются не так уж часто.

К примеру, в 2013 году в штате Кентукки машина протаранила дверь продуктового магазина. Из салона выскочила женщина, сгребла лоток с лотерейными картами (их было полторы тысячи штук) и скрылась. Когда несколько недель спустя ее арестовали, оказалось, что ей удалось выиграть всего двести долларов.

Организаторы лотереи WinFall решили разбить джекпот.

Как только призовой фонд доходил до двух миллионов долларов, а главного победителя не было, объявляли роллдаун, и деньги распределялись между игроками, угадавшими три, четыре и пять чисел.

WinFall давала неплохой шанс получить прибыль, ведь при условии роллдауна на каждый доллар, потраченные на билет, приходилось по меньшей мере 1 доллара 15 центов призовых. 

В феврале 2005 года математик Харви собрал команду из 50 студентов МТИ. Они скинулись примерно на тысячу долларов и на все купили лотерейные билеты. После объявления победителей выяснилось, что команда выиграла втрое больше, чем вложила. В следующие несколько лет игра в лотерею стала для Харви полноценной работой. 

К сожалению, полоса удач продолжалась недолго.

В 2008 году году газета Boston Globe опубликовала статью о лазейках в лотерее и о том, как ими пользуются синдикаты.

Группа МТИ получила преимущество над другими игроками, потому что ее участники понимали механизм игры лучше конкурентов и точнее оценивали шансы на выигрыш.

Долгое время синдикаты использовали тактику выкупа большого количества билетов с разными числовыми комбинациями, известную как «метод перебора».

Метод перебора не требует скрупулезных вычислений. Единственной серьезной проблемой может стать доступ к необходимому количеству билетов.

Если игроки в рулетку стремятся перехитрить только казино, то лотерейные синдикаты сражаются за джекпот с другими похожими синдикатами.

Несмотря на возрастающую конкуренцию, некоторые лотерейные синдикаты продолжают успешно и, главное, законно получать прибыль. Их примеры демонстрируют еще одно отличие лотереи от игры в рулетку: если игроки в рулетку обычно действуют в одиночку или очень небольшой группой, то лотерейные синдикаты часто представляют собой настоящие фирмы.

У них есть инвесторы, они платят налоги. Этот контраст отражает заметный сдвиг в научном подходе к азартным играм – индивидуальные потуги искателей удачи переродились в целую отрасль.

 #ЗнанияСжато #теория вероятностей #Пуанкаре #ошибка игрока  #ложныйвыводМонтеКарло #теорияхаоса #лотерейныеCиндикаты #паттерны #джекпот #методперебора