SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. broker25 |Толстые хвосты и эмпирические распределения. Продолжение
- 14 июня 2013, 11:32
- |
Продолжаю тему, поднятую в статье «Толстые хвосты и эмпирические распределения». Напоминаю, в материале рассматривался вопрос, как влияют толстые хвосты распределения цены базового актива на появление улыбки волатильности. В представленной модели фьючерс РТС каждый день прыгает на величину, случайно выбранную из ряда его ежедневных приращений в прошлом. Ранее были показаны результаты модели для 100 шагов движения цены. К ним мы еще вернемся, а пока рассмотрим, что происходит при небольшом количестве шагов модели. В этом случае, Центральная Предельная Теорема только начинает работать, и толстые хвосты разворачиваются во всей своей павлиньей красе.
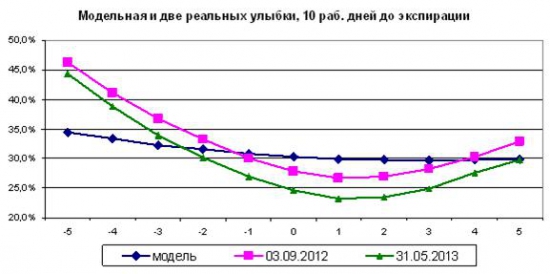
Выше представлена модельная улыбка за 10 дней и две реальных кривых волатильности опционов с аналогичным сроком жизни. Как и раньше, в модели введена поправка на тренд. По оси Х номер страйка от центрального, графики совмещены по горизонтали.
( Читать дальше )

Выше представлена модельная улыбка за 10 дней и две реальных кривых волатильности опционов с аналогичным сроком жизни. Как и раньше, в модели введена поправка на тренд. По оси Х номер страйка от центрального, графики совмещены по горизонтали.
( Читать дальше )
- комментировать
- ★24
- Комментарии ( 8 )
Блог им. broker25 |Толстые хвосты и эмпирические распределения
- 06 июня 2013, 15:15
- |
Финансовые рынки обладают известным свойством – толстые хвосты в распределении приращений актива. Обычно, для демонстрации эффекта сравнивают два графика дневной доходности – для исторического распределения цен и нормального. На рисунке ниже четко заметны выбросы в распределении доходности индекса вдалеке от центра.

Часто можно услышать, как толстые хвосты назначают главной причиной возникновения улыбки волатильности. На недавно прошедшей НОК одним из наиболее интересных выступлений была презентация Виталия Курбаковского о причинах появления улыбки волатильности. Уважаемый мэтр строил улыбку на основе эмпирического распределения.
Проверим сами, как влияют толстые хвосты на форму улыбки. Построим модель движения фьючерса РТС на основе данных о ежедневной доходности close to close основной сессии. Возьмем ряд ежедневных приращений склеенного фьючерса с января 2010г. по февраль 2013г. Конечное значение цены близко к начальному, но, чтобы совсем исключить тренд, последнее значение цены фьючерса примем равным первому, а именно 157090 п. Период модели – 100 дней. Каждый день актив прыгает на величину, случайно выбранную из ряда прошлых значений. В конце траектории посчитаем стоимость опционов. Повторим опыт миллион раз. Усредним результаты каждого опыта и получим ожидаемую стоимость опционов в финальной точке. Она совпадает со справедливой стоимостью опционов в начальной точке, ведь ставка равна нулю. Результат моделирования в терминах волатильности представлен ниже

( Читать дальше )

Часто можно услышать, как толстые хвосты назначают главной причиной возникновения улыбки волатильности. На недавно прошедшей НОК одним из наиболее интересных выступлений была презентация Виталия Курбаковского о причинах появления улыбки волатильности. Уважаемый мэтр строил улыбку на основе эмпирического распределения.
Проверим сами, как влияют толстые хвосты на форму улыбки. Построим модель движения фьючерса РТС на основе данных о ежедневной доходности close to close основной сессии. Возьмем ряд ежедневных приращений склеенного фьючерса с января 2010г. по февраль 2013г. Конечное значение цены близко к начальному, но, чтобы совсем исключить тренд, последнее значение цены фьючерса примем равным первому, а именно 157090 п. Период модели – 100 дней. Каждый день актив прыгает на величину, случайно выбранную из ряда прошлых значений. В конце траектории посчитаем стоимость опционов. Повторим опыт миллион раз. Усредним результаты каждого опыта и получим ожидаемую стоимость опционов в финальной точке. Она совпадает со справедливой стоимостью опционов в начальной точке, ведь ставка равна нулю. Результат моделирования в терминах волатильности представлен ниже

( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















