ipsnow
Торговля постоянной суммой может изменить матожидание ТС?
- 09 апреля 2024, 02:09
- |
Понятно, что постоянная сумма в сделке вносит нелинейность в отображение Ценовой график -> Эквити, но чтобы менять МО — это как-то неожиданно.
Т.о. выбор того, постоянная сумма или постоянный лот — часть торговой стратегии, от которой может зависеть ее прибыльность/убыточность..
При этом постоянный лот сильно меняет эквити, если инструмент сильно меняет со временем свое значение. И вообще непонятно, чье поведение при разработке тестера в итоге проще будет учесть.
- комментировать
- Комментарии ( 0 )
Торговля синусоиды по стопам, математическая задачка
- 07 апреля 2024, 23:07
- |
Вопрос: как будет выглядеть эквити алгоритма, который покупает, держит позицию до стопа, закрывается (потом сразу снова покупает и тд) если запустить его на графике синусоиды? Без комиссии и если стоп:
- по времени удержания позиции (т.е. держит N свечей)
- по абсолютному изменению цены (т.е. как только цена изменилась на N% от входа в сделку)
UPD: чтобы избежать деления на ноль во втором пункте определим график как f(x) = sin(x) + 2
А как посчитает среднюю сделку Ваш бэктестер?
- 25 декабря 2021, 15:59
- |
И такие сделки: купить 1шт, купить 1шт, продать 2шт.
Итого, первая сделка принесла 21%, вторая — 10%. Очень хотелось было бы посчитать среднюю как (21%+10%)/2 = 15.5%. Очень — потому что это число легко интерпретировать. Например, понятно, на сколько изменится финрез, при изменении комиссии. Или сколько мы заработаем на 1000 таких сделках. Для такого подсчета бэктестер должен хранить историю сделок, а не просто среднюю цену.
Если же посчитать итоговый результат по отношению к используемому капиталу (100+110), то результат сделки можно оценить как (121*2-100-110)/(100+110) = 15.2%. Т.е. интерпретируем вторую сделку как усреднение первой (а это самая простая реализация бэктестера). И это уже комплексная величина, учитывающая плечо, и которой ментально оперировать сильно труднее.
Отсюда вопрос, какую среднюю используете Вы?
Hands-On Deep Learning for Finance
- 28 июля 2020, 13:00
- |
Я бы вместо чтения этой книги посоветовал поиграть с любым гитхаб-репозиторием на эту тему + прогуглить все незнакомые слова. Для «Hands-On» подойдет намного лучше.
Как долго сохраняется распределение приращений цен?
- 02 июня 2020, 14:09
- |
Продолжаю экспериментировать с распределением ценовых приращений. Задался вопросом, насколько быстро меняется распределение в зависимости от:
1) размера выборки
2) соотношения «размер тестовой выборки / (размер основной + тестовой выборки)»
Техника простая — разбиваем серию минуток на перекрывающиеся интервалы, каждый интервал разбиваем на две части — основную выборку и тестовую, проверяем, отличается ли первая от второй. И так для каждой акции, размера целой выборки, размера тестовой выборки.
Перед отображением на графике результаты усредняем.
Факт изменения распределения определялся тестом Колмогорова-Смирнова.
Ниже — графики зависимости изменчивости распределения от размеров выборки (тестовой и совокупной)
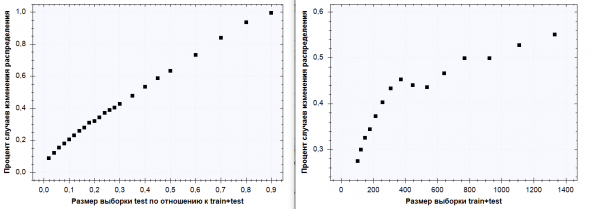
Замечу, что при небольших размерах выборки результаты на левой части графика становятся недостоверными (минимальный набор для теста Колмогорова-Смирнова ~ 30).
( Читать дальше )
Динамика распределения ценовых приращений в GIF
- 29 мая 2020, 13:56
- |
Картинки сгенерированы для медитации, без выводов :)
Таймфрейм — минутки с 2009 по 2018г, один фрейм — распределение приращений за полгода. Для удобства восприятия выкинуты returns: нулевые и выходящие за третий квантиль. Ось по горизонтали подписана в долях от процента.


( Читать дальше )
Не все RL алго одинаково полезны
- 30 апреля 2020, 22:23
- |
Кроме дельных замечаний от бывших квантов, узнал из комментов про фатальный недостаток A3C — теоретическую малоприменимость в состязательных средах:
An additional problem with this is that they use A3C here for trading. A3C is known to not be suitable for adversarial environments (e.g. board games, like Chess). I wrote a paper that demonstrated that A3C is as exploitable as a uniform random strategy in board games (specifically, some poker variants): arxiv.org/abs/2004.09677
It’s mostly an issue that A2C isn’t designed for adversarial environments. It also doesn’t have any notion of hidden information, while other algorithms (eg CFR) explicitly handle this. There’s a well-known phenomena of cycling, where agent A will beat agent B which beats agent C which beats agent A; A2C can exhibit this. Think of rock/paper/scissors- AlwaysRock beats AlwaysScissors which beats AlwaysPaper. To avoid this, you typically need to do some sort of averaging.
link
Понятно, что многие алго из описанных в интернете можно доработать и построить на их основе рабочую стратегию. Так что не принимаем это близко к сердцу и продолжаем экспериментировать.
В поддержу простоты предсказательных моделей
- 02 апреля 2020, 17:39
- |
Общеизвестно, что чем метод проще, тем он надежнее (в контексте предсказаний — точнее). Комментаторы смартлаба через один утверждают это, но сколько из них обосновывают свои утверждения?
Решил изучить этот вопрос подробнее. Ключевые ссылки нашел в ответах на вопрос https://stats.stackexchange.com/questions/124955/is-it-unusual-for-the-mean-to-outperform-arima (чувак спрашивает, нормально ли, что в его исследованиях лучше работают простые методы типа скользяшек). Помимо множества цитат авторитетов научного мира приведено любопытное исследование от 2015г (цифры округлены, т.к. немного гуляют даже в пределах публикации):
В отличие от некоторых дискуссий, по нашему определению сложность не является функцией от количества переменных. Сложность также не зависит от усилий, необходимых для разработки модели. Чтобы выяснить, прост ли метод прогнозирования, мы спрашивали его пользователей, понимают ли они его — и если да, то смогут ли объяснить, задействованные в модели математические методы, как эта модель представляет исходную информацию, как разные части модели связаны друг с другом и как прогноз модели поможет принять лучшее решение.
( Читать дальше )






















