Блог им. mihaylets |Стоит ли бояться больших текущих оценок рынка? Что такое «нормализация»
- 15 марта 2021, 10:45
- |
Хотел бы я быть первым, кто скажет вам о том, что рынке сейчас дорогие, но, видимо, не в этот раз. «Дорогие рынки» — сегодня уже устойчивое выражение. Но главный вопрос в том, а стоит ли этого бояться? И да, и нет.
По истории после кризисов в период восстановления, фондовый рынок всегда опережает восстановление экономики, что по истории приводит к росту его оценочной стоимости. Но эта «переоцененность» исторически не приводит к его падению, а вызывает так называемую нормализацию. Когда получив аванс, компании должны показать реальный рост прибылей. В этот момент времени с ростом фактических показателей, происходит нормализация оценок, по которым торгуется рынок.
Это же означает, что стоимость акций практически не растет. Ниже на графике указана доходность (без учета дивидендов), которую получили инвесторы во время нормализации. В предыдущие три кризиса доходность рынка в период нормализации была около нулевой.
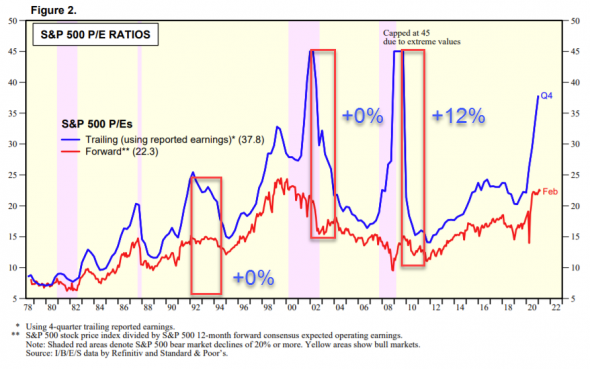
( Читать дальше )
- комментировать
- ★2
- Комментарии ( 1 )
Блог им. mihaylets |Тонкости сравнительного анализа компаний, мультипликатор P/E и его «внутренности»
- 08 января 2021, 13:20
- |
Многие любят сравнительный анализ из-за его простоты и быстроты использования. Достаточно нескольких минут, чтобы понять дорогая или дешевая компания. Но, как и в любом деле, тут также есть свои нюансы, об одном из которых я и хотел бы рассказать в этой статье. Речь пойдет о, наверное, самом известном мультипликаторе P/E.
Сам мультипликатор незамысловат и вычисляется как стоимость всех акций компании, деленная на прибыль компании. Либо же цена акции, деленная на прибыль на одну акцию. Это мультипликатор показывает вам окупаемость ваших инвестиций при неизменности показателей компании, сколько лет вам будет нужно, чтобы полностью вернуть свои вложения. Для примера P/E Tesla 1496, это значит, что если прибыль компании не изменится, то вы окупите свои вложения только через полторы тысячи лет. Что говорит о том, что покупка акций Tesla при текущих значениях, выглядит довольно долгосрочной инвестицией.
Теперь к нюансам. Этот простой мультипликатор можно представить по-другому, через формулу Гордона для сформированных компаний (Tesla не совсем подходит, но на ее примере очень хорошо будет понята вся суть этой статьи). Сама формула выглядит как:
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















