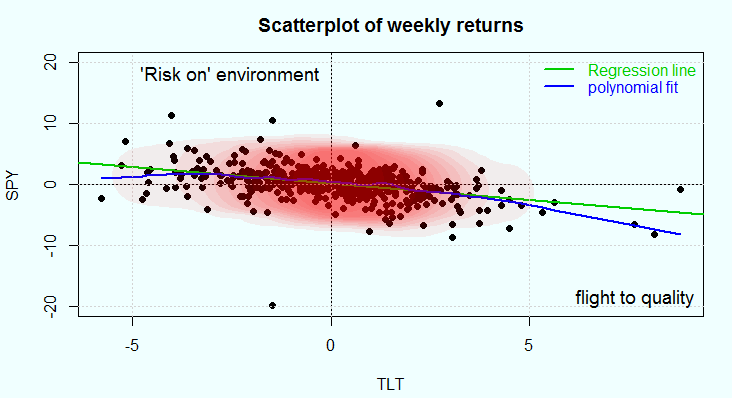
Интересные соображения по поводу вычисления правильной корреляции изложил в своем блоге Eran Raviv. По моему мнению данный подход можно попробовать использовать в статистическом арбитраже и парном трейдинге. Ниже даю полный перевод статьи с кодом на языке R.

В случае постоянной скорости, время и расстояние полностью коррелированы. Дайте мне одну переменную, я дам вам другую. Когда две переменные не имеют ничего общего между собой, мы говорим, что они не коррелированы.

Вы думаете, что это все, что можно сказать, но это не так. Как правило, ситуация более сложная. В большинстве обычных применений используется корреляция Пирсона. Коэффициент корреляции Пирсона отражает линейную зависимость. Поэтому мы говорим, что это параметрический показатель. На самом деле он может возвращать ноль даже если две переменные полностью зависимы ( наглядно показано здесь).

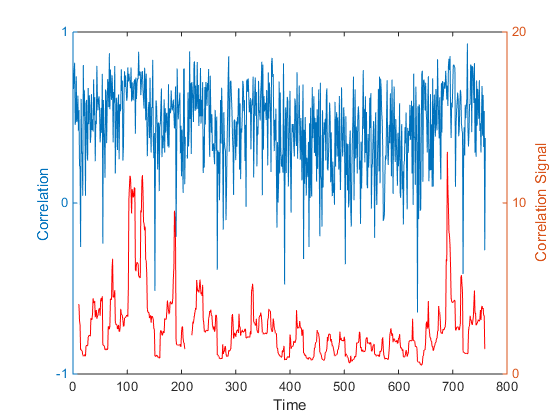
Использование корелляции широко распространено в финансовой теории и практике, от создания портфелей до стратегий статистического арбитража.

Основная сложность в применении корелляции это ее изменчивость: активы, которые в один момент времени кажутся практически некоррелироваными для целей хеджирования, могут стать высококореллироваными в другие моменты времени, например, при высокой активности рынка. Напротив, акции, кажущиеся подходящими для парной торговли, в связи с высокой корелляцией их приращений цены, могут позднее показать разнонаправленную динамику, приводящую к значительным потерям.

Нестабильность уровня еще усугубляется эмпирическими выводами о том, что волатильность корреляции сама по себе зависит от времени: в одно время корреляция между активами может плавно меняться в узком диапазоне, в другое время мы можем наблюдать  изменения знака коэффициента корелляции в течении нескольких дней.