Избранное трейдера Marco
Стратегия с классификацией ордеров по времени жизни. Часть 1
- 22 мая 2015, 13:52
- |
Неплохую идею для высокочастотного трейдинга подсказал Kipp Rogers в своем блоге. Идея несложная, но требующая подробного объяснения, поэтому попробую изложить ее в двух статьях.
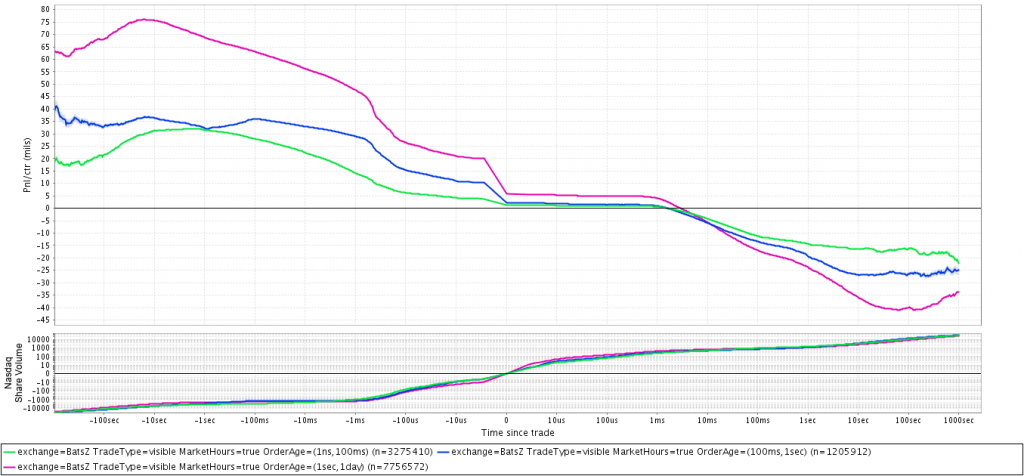
Автор предположил, что лучшее исполнение ордеров, отправленных на биржу, скорее возможно получить, торгуя с трейдерами — людьми, вручную отправляющими приказы, чем с компьютерами, то есть контрагентами с автоматическим выставлением. Высокочастотные роботы отправляют приказы на биржу только в том случае, если они видят возможность быстрого снятия прибыли или ищут наилучшую цену исполнения для больших объемов, что делает соревнование с ними очень тяжелой задачей. С другой стороны, трейдеры, торгующие вручную ( под ними могут подразумеваться и автоматические программы с медленными алгоритмами ), выставляют приказы с большим временем жизни (до отмены или исполнения), меньше внимания уделяют мгновенной цене и, как правило, имеют идею о направлении движения цены при входе в рынок, что также дает представление о поведении их ордеров.
( Читать дальше )
- комментировать
- ★26
- Комментарии ( 15 )
Модель скрытых состояний Маркова. Часть 4
- 20 мая 2015, 14:06
- |
Окончание цикла статей. Начало и другие алгоритмы биржевой торговли смотрите в моем блоге и на сайте.
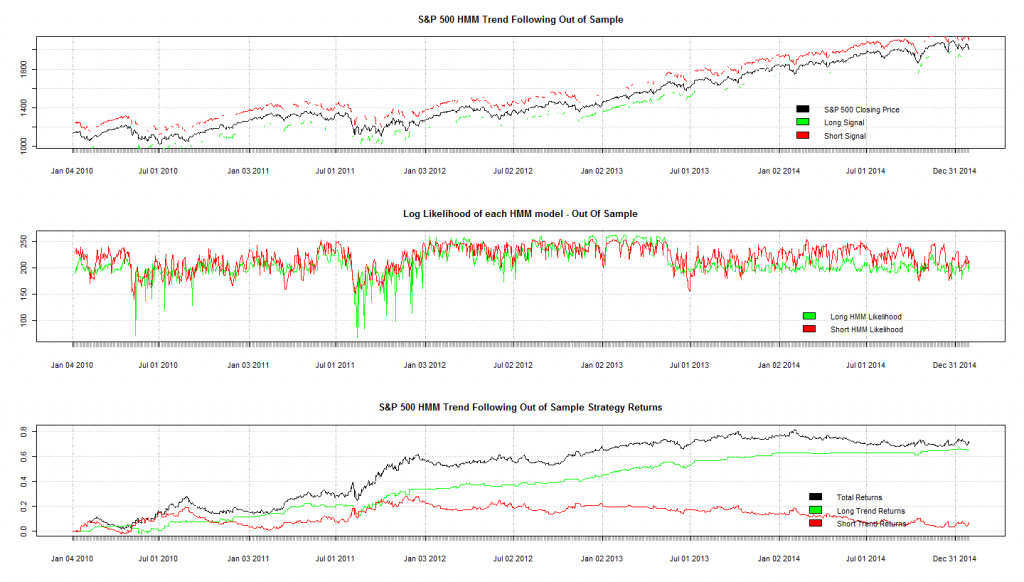
В прошлой части мы продемонстрировали обучение модели Маркова на данных, полученных с помощью симуляции. В данной статье рассмотрим производительность модели на реальных данных. Будем тестировать трендследящую стратегию на индексе S&P500.
В большинстве задач с использованием машинного обучения требуются обучающие данные с разметкой классов (состояний). В нашем случае такой разметки нет, поэтому сначала сгенерируем классы для обучающей выборки.
Мы хотим создать трендследящую стратегию, поэтому должны выбрать участки на выборке цен S&P500, которые соответствуют восходящему и нисходящему трендам ( также можно отметить участки, где тренды отсутствуют). Можно это сделать вручную, а можно применить программу, которая автоматически расставит метки в соответствии с вашими определениями тренда.
( Читать дальше )
Модель скрытых состояний Маркова. Часть 3
- 18 мая 2015, 14:01
- |
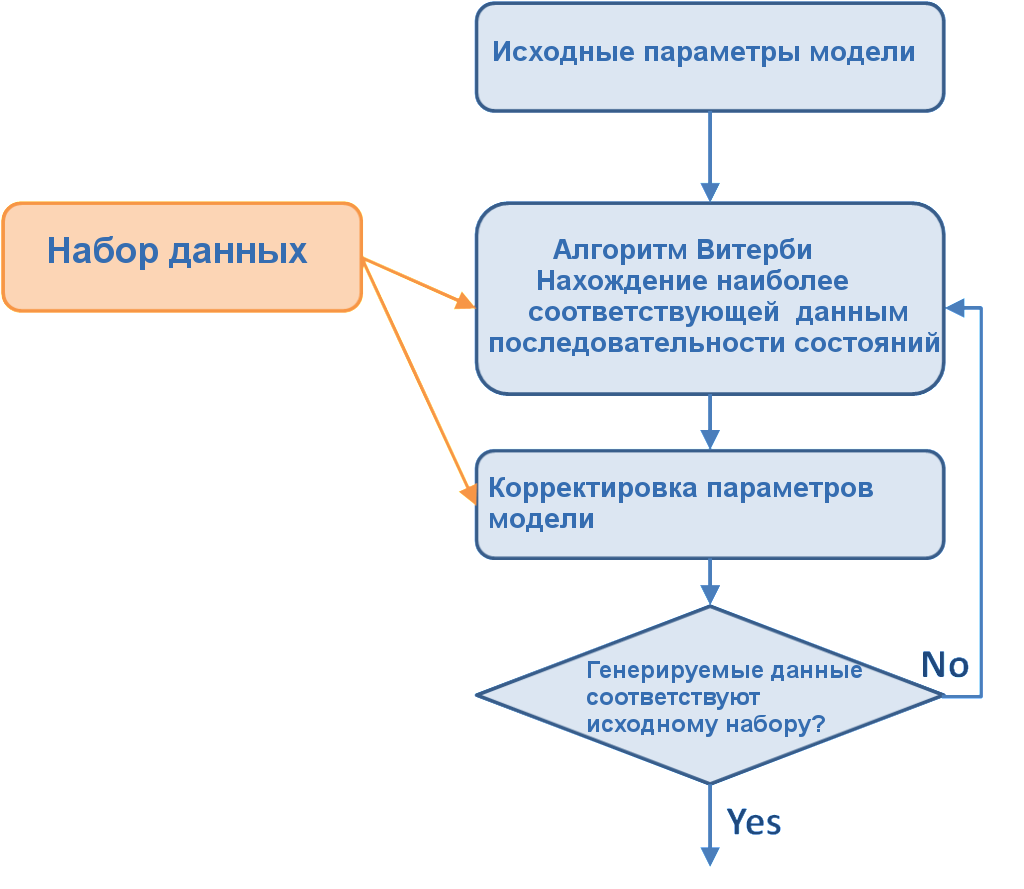
В этой части рассмотрим обучение модели скрытых состояний Маркова на языке R. В прошлых статьях мы изучили математическую основу модели, которая воплощена в библиотеке RHmm. Есть два способа распознавания режимов с помощью модели Маркова, первый — использование одной модели, каждое состояние которой отражает режим, в каком находится рынок. Второй способ подразумевает построение нескольких моделей, каждая из которых создана для одного режима, задача состоит в том, чтобы выбрать ту модель, которая генерирует данные, наиболее соответствующие текущему состоянию рынка. Рассмотрим оба эти способа.
Метод первый — одна модель с несколькими состояниями.
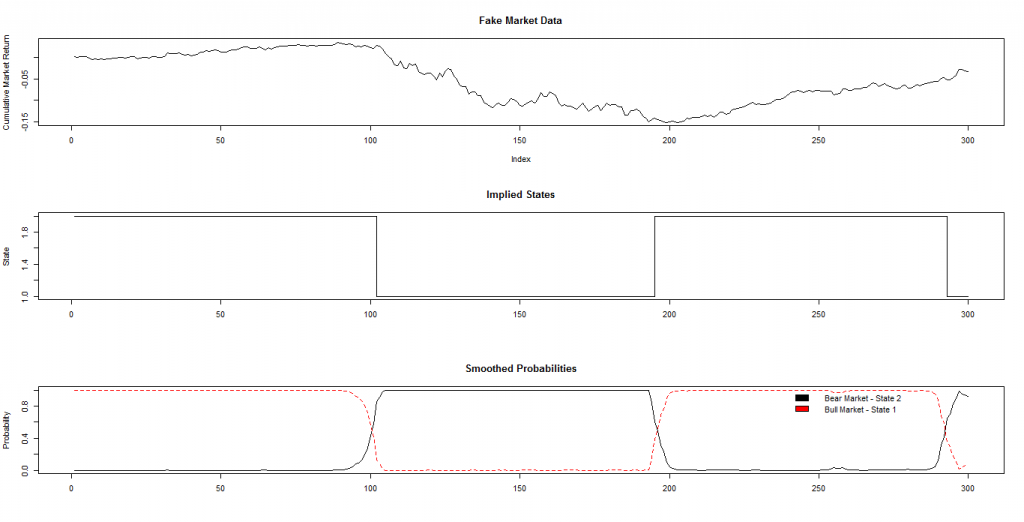
Для обучения модели будем использовать исходные данные, полученные симуляцией из нормального статистического распределения N(mu,sigma), где mu — медиана, sigma — среднеквадратичное отклонение. Распознавание будем производить для двух режимов — бычьего (bull) рынка, на котором наблюдается восходящий тренд и медвежьего (bear) рынка, на котором тренд нисходящий. Соответственно, сгенерируем приращение значений из двух нормальных распределений - N (mu.Bull,sigma.Bull) и N(mu.Bear,sigma.Bear). На рисунке показан результат такой генерации на 300 наблюдений, 100 первых из которых получены из бычьего распределения, 100 вторых — из медвежьего и 100 последних — из бычьего с другими параметрами mu и sigma (каждое приращение будем считать дневным):
( Читать дальше )
Модель скрытых состояний Маркова. Часть 2
- 14 мая 2015, 13:34
- |
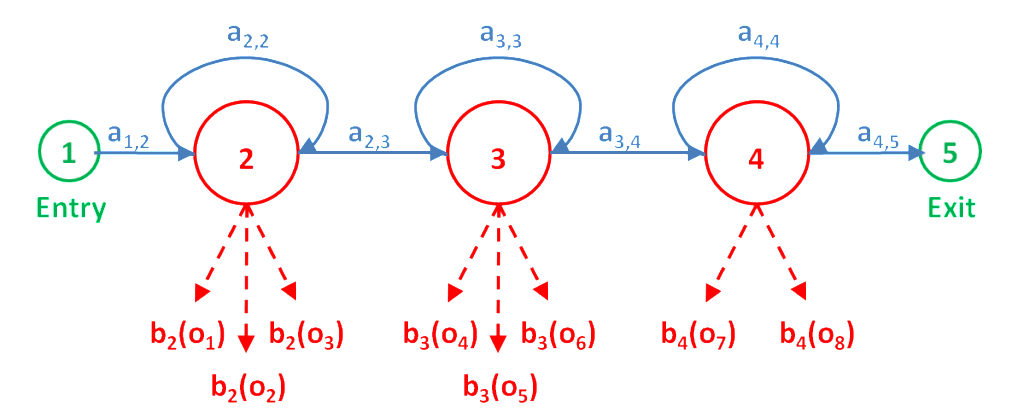
В предыдущей статье мы говорили об эффективных алгоритмах, необходимых для вычисления вероятностей и стат. распределений модели Маркова, которыми являются форвардный алгоритм и алгоритм Витерби. Форвардный алгоритм вычисляет вероятность соответствия данных наблюдения полученным моделью всем возможным последовательностям состояний. Алгоритм Витерби вычисляет вероятность соответствия данных полученной моделью одной, наиболее вероятной, последовательности.
В этом посте будет много формул, но без этого не обойтись, чтобы создать хорошую стратегию, надо разбираться в математической модели, лежащей в ее основе. Следующие части будут более приближенными к практике.
Форвардный алгоритм.
Форвардный алгоритм позволяет эффективно рассчитать функцию вероятности p(O|λ). Форвардной переменной называется вероятность генерации моделью наблюдений до времени t, и состояние j в момент времени t определяется как:
( Читать дальше )
Модель скрытых состояний Маркова. Часть 1
- 12 мая 2015, 14:35
- |
В данном цикле статей начинаем рассматривать модель Маркова, которая находит применение в задачах классификации состояния рынка и используется во многих биржевых роботах. Статьи основаны на постах, опубликованных в блоге Gekko Quant. Также будет рассмотрены практические алгоритмы на финансовых рынках. Код в цикле приведен на языке R. Вначале будет много теории, ее надо хотя бы попробовать понять, затем разберем практические примеры.
Рабочая среда распознавания основных паттернов.
Рассмотрим набор признаков O, полученный из набора данных d и класс w, обозначающий наиболее подходящий класс для O:
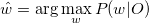
( Читать дальше )
Линейная регрессия с использованием фильтра Калмана
- 23 апреля 2015, 10:12
- |
Линейная регрессия часто используется для вычисления пропорции хеджирования в парном трейдинге. В идеальной ситуации коэффициенты этой регрессии — наклон линии регрессии и свободный член (пересечение) остаются всегда постоянными. Однако в реальности все, конечно, не так радужно, и значения этих параметров постоянно меняются во времени. Как правильно вычислять коэффициенты регрессии, чтобы избежать подгонки к текущей ситуации, рассматривается в статье "Online Linear Regression using a Kalman Filter". Для этой цели в данной публикации используется фильтр Калмана.
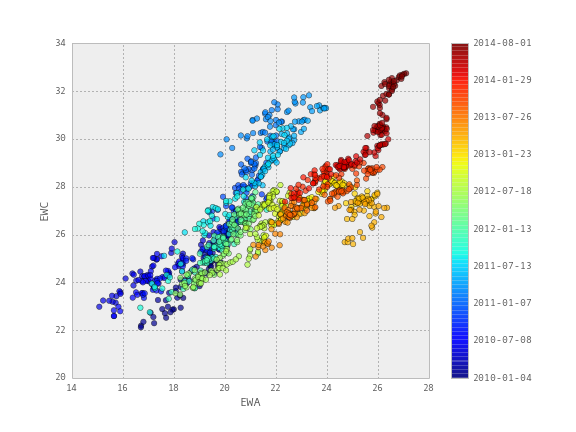
Для тестирования берутся исторические цены закрытия двух биржевых фондов ETF — австралийского EWA и канадского EWC с 2010 по 2014 год. Динамика цен этих фондов показывает взаимосвязь, что продемонстрировано на диаграмме рассеивания в заглавии поста. Однако по этому же графику видно, что эту взаимосвязь невозможно описать с помощью линейной регрессии с постоянными коэффициентами.
( Читать дальше )
Модернизация стратегии robot_uralpro. Lead-lag relationship
- 16 апреля 2015, 10:22
- |
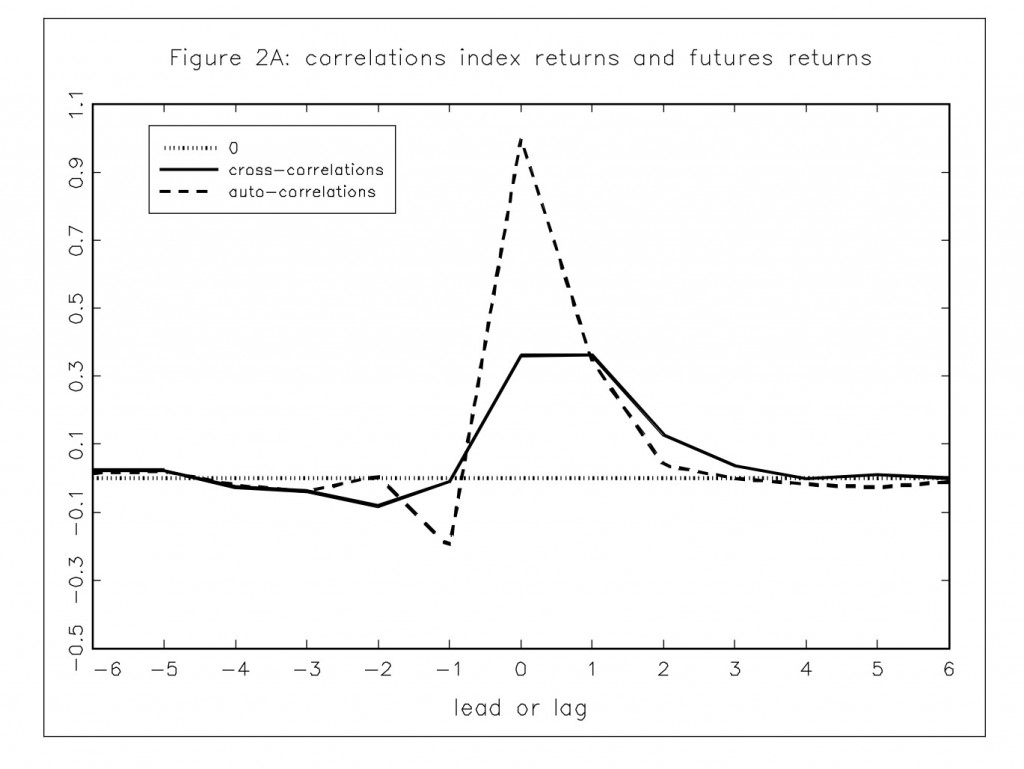
Трейдеры, которые приобрели мою программу robot_uralpro (см. пост на смарт-лабе), спрашивают, можно ли доработать алгоритм для применения его на современном рынке? Напомню, стратегия робота основана на взаимоотношении цен синтетического индекса, составляемого динамически из рыночных цен акций, входящих в индекс РТС, и фьючерса RI. Идея «одноногого» статистического арбитража, реализованного в роботе, будет работать и сейчас, только в том случае, если научиться правильно определять, какой актив опережает другой в смысле динамики их цен. Эта статья посвящена правильному выявлению такого взаимодействия, которое в англоязычных источниках называется «lead-lag relationship» -опережение-отставание между разными активами.
Те алготрейдеры, кто не приобретал robot_uralpro, тоже сочтут эту статью полезной, так как lead-lag relationship может использоваться в стратегиях парного трейдинга и им подобным. Например, определив такое взаимодействие, можно исключить из парного трейдинга один из активов ( с учетом того, конечно, что отношение торгуемых инструментов было описано четкой моделью) и значительно увеличить тем самым прибыльность стратегии.
( Читать дальше )
Алгоритмы маркетмейкера. Часть 5
- 09 апреля 2015, 11:27
- |
Продолжаем разбирать численное решение уравнения Хамильтона-Якоби-Беллмана. В прошлой части мы составили выражение для оператора 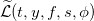 , в котором есть слагаемые, получить значение которых можно из реальных данных. Во-первых, что из себя представляют дифференциальные матрицы D1,D2. Это матрицы размерностью
, в котором есть слагаемые, получить значение которых можно из реальных данных. Во-первых, что из себя представляют дифференциальные матрицы D1,D2. Это матрицы размерностью 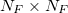 , где, для D1(согласно определению в части 4) в ячейках [j,j] стоят -1, если fj<0 и 1 в остальных случаях, в ячейках [j,j+1] стоят 1, если fj<0 и 0 в остальных случаях, и в ячейках [j,j-1] стоят -1, если fj≥0 и 0 — в остальных случаях. Как составить матрицу D2, я думаю, вы догадаетесь сами, взглянув на ее определение в
, где, для D1(согласно определению в части 4) в ячейках [j,j] стоят -1, если fj<0 и 1 в остальных случаях, в ячейках [j,j+1] стоят 1, если fj<0 и 0 в остальных случаях, и в ячейках [j,j-1] стоят -1, если fj≥0 и 0 — в остальных случаях. Как составить матрицу D2, я думаю, вы догадаетесь сами, взглянув на ее определение в
( Читать дальше )
Алгоритмы маркетмейкера. Часть 4
- 07 апреля 2015, 11:25
- |

Прошлые части цикла здесь. В этой части статьи мы найдем численное решение системы уравнений оптимального управления позицией маркетмейкера. Такое решение легко запрограммировать и использовать в реальной торговле для контроля за лимитными и маркет ордерами в соответствии с полученными стратегиями θmk,θtk. Для упрощения разложим функцию владения на слагаемые, чтобы получить сокращенную функцию владения v(t,y,f,s), которая представляет собой только динамическую составляющую основной функции:
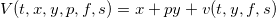
( Читать дальше )
Алгоритмы маркетмейкера. Часть 3
- 02 апреля 2015, 09:46
- |
Продолжаем разбирать работу JIANGMIN XU «Optimal Strategies of High Frequency Traders». Чтобы составить уравнение оптимального контроля, сначала сформулируем проблему оптимизации алгоритма при используемых стратегиях θ, как достижение максимума следующего матожидания:
![Алгоритмы маркетмейкера. Часть 3 \max_{\theta^{mk},\theta^{tk}}\mathbb{E}_0[X_T-\gamma\int^T_0 Y^2_{t-}d[P,P]_t]](http://mathurl.com/pthr6jr.png) ,
,
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лидеры роста и падения ммвб
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- си
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трейдер
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал