Избранное трейдера Romario_
Несколько неудобных вопросов, касающихся методов расчета справедливой стоимости опционов. Второй вопрос.
- 04 декабря 2018, 16:11
- |
- 1. Что такое кривая волатильности и как она соотносится с моделью БШ
Все знают, что такое ожидаемая волатильность опциона (Implied Volatility). Это волатильность, которую нужно подставить в формулу Блэка-Шолеса, чтобы получить текущую рыночную стоимость опциона. Вычислив ее для всех страйков, можно затем аппроксимировать полученные значения гладкой параметрической кривой – кривой волатильности.
Но, если при расчете кривой волатильности мы всегда и везде используем формулу БШ, то мы так же всегда и везде должны доверять ее авторам, а они утверждали, что волатильность опционов должна в точности равняться волатильности базового актива, которая может быть только одна. Откуда взялась кривая? Либо мы верим Блэку и Шолесу (должна быть прямая), либо не верим (тогда кривая).
У кривой волатильности нет содержательного смысла. Это простая подгонка. Единственным ее назначением является устранение расхождений между теоретическими и рыночными ценами. Какую бы модель ценообразования опционов мы ни взяли, кривая волатильности исправит все ее огрехи. Что-то вроде толстого слоя штукатурки, с помощью которого можно выровнять любую стену.
При этом мы полностью лишены возможности отличить хорошую модель от плохой, после использования кривой расчетные цены любой модели будут близки к рыночным. Тогда почему мы пользуемся именно моделью БШ? Видимо, потому, что де-факто она признана стандартной.
- комментировать
- ★8
- Комментарии ( 16 )
Несколько неудобных вопросов, касающихся методов расчета справедливой стоимости опционов. Первый вопрос.
- 04 декабря 2018, 15:55
- |
Несколько неудобных вопросов, касающихся методов расчета справедливой стоимости опционов.
В теории опционов ключевую роль играет понятие теоретической или справедливой цены. Чем правильнее она рассчитана, тем выше шансы игрока на получение прибыли. Обилие математики в опционных расчетах убеждает, что именно профессиональные математики должны преуспевать в этой игре. Не ставя под сомнение последнее утверждение, сформулирую несколько вопросов, ответов на которые и сам, вообще-то, не знаю. Вопросы, тем не менее, важные. От ответов на них зависит, вправе ли мы использовать аппарат ТВиС при нахождении справедливых цен опционов.
1. Насколько оправдано использование математического ожидания при нахождении справедливой стоимости опционов
При расчете справедливой цены опциона (то есть цены, не дающей преимущества ни одной из сторон) используется соотношение:
MO[выигрыш продавца] = MO[выигрыш покупателя] = 0
Почему именно матожидание? Ответ вроде бы очевиден – потому что это самая содержательная и самая удобная из всех числовых характеристик случайной величины. Теперь рассмотрим пример.
( Читать дальше )
Как вывести деньги с ИИС
- 29 ноября 2018, 12:14
- |
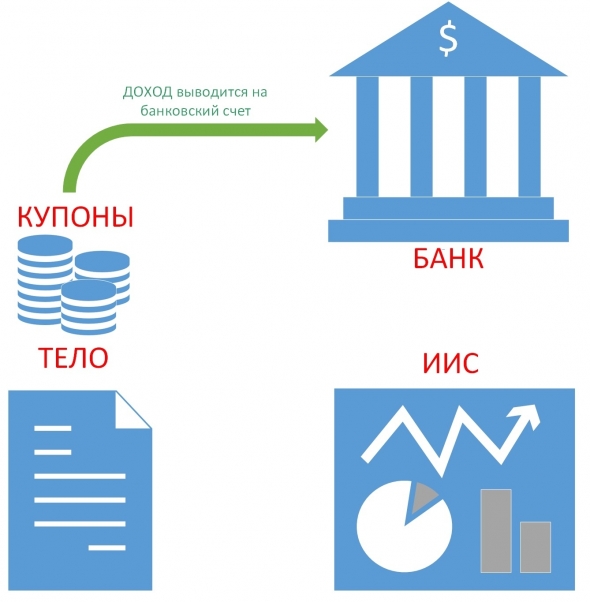
Как все знают, деньги с ИИС нельзя выводить в течение 3х лет. Это — единственная причина, почему ИИС ещё не открыл каждый работающий россиянин :) На самом деле, способы вывода денег с ИИС есть. Их три, и каждый из них имеет свои особенности:
- Дивидендный комбайн
- Купонный комбайн
- «Свистящие» облигации
Дивидендный комбайн
Первый способ, открытый и опробованный на практике в 2016 году. Для работоспособности нужно, чтобы брокер позволял выводить дивиденды на банковский счёт, а такую возможность дают не все брокеры. Суть в том, чтобы заходить в акцию перед отсечкой. Далее акция попадает на дивидендный гэп, который плюс-минус равен дивиденду, полученному на банковский счёт с учётом налогов. Акция продаётся сразу на гэпе.
В результате сальдо не меняется (или меняется несущественно), а деньги просто перемещаются из левого кармана инвестора в правый.
( Читать дальше )
Какой семейный авто купить за 1 млн руб?
- 28 ноября 2018, 12:19
- |
Какие кстати есть льготы, кто в курсе?
Но главный вопрос не в этом. Семья теперь уж точно не влезает в мою теану и мне нужен какой-нить полуавтобус.
Я уже писал посты на тему:
Как надо покупать машину:) ★32, 10к просм, +476 391K
А как оценить предельную стоимость машины, которую я могу себе позволить? ★13, 6,3к просм
Меня прям разрывают противоречия. Вот потратить на машину лям еще куда не шло. Продать теану, будет уже 1,6-1,7 лям.
За эти бабки можно купить уже какой-нить не очень ушатанный БУшный Хёндай старекс с выдающейся вместительностью или слегко подушатанный Мультиван (жене нравится его дизайн). Посмотрел ескалейды и тахо — даже предложений то приличных за эти деньги нет, одни перекупы на авто.ру)) Смотрел также Dodge Caravan 2010… Ну тож убитый наверное будет, страшно брать. Хотя тачка для моих задач норм.
Но и продавать теану за 0,6-0,7 лям очень жалко, слишком хорошая тачка:( После нее любая тачка покажется ведром… (ну кроме эскалейда)
Содержать две тачки — слишком дорого и неразумно. Кроме того, за лям можно будет купить только 2008-2010 год, а значит будет разваливаться постоянно...
А как бы вы решили задачу с такими исходными данными?:)
Что сказал Ларри
- 25 ноября 2018, 22:53
- |
И решил оставить здесь, у себя в смарт-дневнике некоторые выписки и цитаты из его выступления, чтобы возвращаться к ним время от времени.
Ничего нового он в общем то не сказал, все главные правила работы для достижения прибыльной торговли были сказаны им ранее и сейчас были снова повторены.
И все эти правила работы написаны для трейдеров-спекулянтов на фьючерсах (инвесторам далее можно не читать, у инвесторов свой путь коллекционеров акций). И вот все эти правила вместе и могут называться Граалем спекулянта, который все упорно ищут.
Сам Ларри сказал о себе следующее: я позиционный трейдер, я не дейтрейдер (далее все выдержки и где-то цитаты от Ларри будут выделены синим цветом и написаны курсивом), ежедневно я проверяю свои позиции, смотрю где мои цели, где мои стопы, смотрю что происходит, что можно купить/продать, есть ли новые возможности, где можно войти. Каждый трейд для меня равный, либо он будет в +, либо в -, самое главное – это контролировать деньги.
( Читать дальше )
Спекуляции без технического анализа. Подробное описание.
- 25 ноября 2018, 10:42
- |
Доброго времени суток, коллеги!
К сегодняшнему дню подготовил объемный и подробный материал, который, возможно, перевернет ваше представление о спекулятивной торговле, откроет новые возможности и даст пищу для ума. Для кого — то, безусловно он будет сухим, не новым и бесполезным.
Скорее всего – это мой последний пост на смарт – лабе, который так или иначе будет относится к теме спекуляций. Данную тематику полностью перевожу в свою группу ВК.
Ни в коем случае не гарантирую работоспособность своего подхода и не утверждаю, что это Грааль, но с уверенностью могу сказать, что лично мне он помогает и работает на трендовом рынке.
Это один из возможных подходов, при использовании которого увеличивается вероятность заработать копеечку в хаосе и беспорядке на рынке.
Речь пойдет о моей практической спекулятивной торговле, где я не использую технический анализ. Да. Вы правильно прочитали. Я не использую технический анализ.
Понимаю, что разговоры о том, работает технический анализ или не работает – бессмысленны. В этой статье я не буду доказывать его неработоспособность.
( Читать дальше )
Конец безумия: Рублебочка вернулась на начало апреля.
- 23 ноября 2018, 16:33
- |
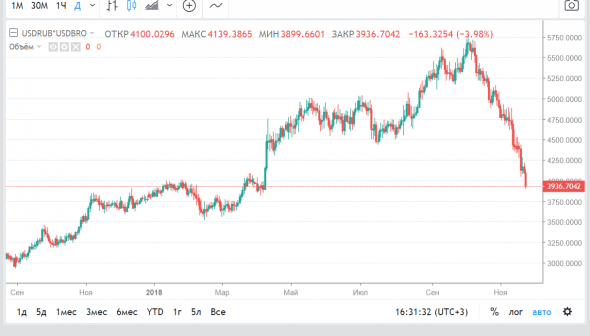
Ура, рублебочка снова стоит 3900 руб. Я тут посчитал: с 9 апреля, чуть больше чем 220 дней цена нефти Брент в рублях была в среднем 5000 руб/баррель. Не знаю сколько стоит российская нефть, но она также 220 дней была примерно на 1000 руб/баррель дороже апрельской. При добыче в РФ около 10 млн.барр/день это 2,2 трилиона рублей или 33 млрд.долларов «лишних» доходов. Не знаю куда их дели, надеюсь уже строится 30 новых яхт, но населению они точно не перепали. Если так пойдет и дальше, то в январе мы увидим 2000 руб/баррель, что конечно невероятно, но вдруг.
Госдума одобрила налоговый режим для самозанятых
- 23 ноября 2018, 16:30
- |
15 ноября Государственная Дума одобрила введение нового налогового режима — налога на профессиональный доход, или «налога для самозанятых». Если связанные с режимом законопроекты утвердят Совет Федерации и президент РФ, на него можно будет перейти с 1 января 2019 года.
Тексты законопроектов и ход обсуждения: раз, два и три
Кто может воспользоваться режимом и зачем это делать. Самозанятые — это физлица, которые продают произведенные товары или оказывают услуги, и ИП без наемных работников. Выбрав новый режим, они могут уменьшить сумму уплачиваемого налога.
Что платят сейчас:
- Физлица — НДФЛ со ставкой 13%.
- ИП — зависит от выбранного режима. Например, 6% от дохода или 15% от прибыли при упрощенной системе налогообложения.
( Читать дальше )
Что происходит с нефтью?
- 14 ноября 2018, 10:16
- |

Данные отслеживания перемещения судов, показывают, что поставки нефти в Азию выросли с января 2017 года на 15%, и на 5% с января 2018. Большая часть этой нефти была заказана накануне санкций против Ирана. Но неожиданно санкции оказались слабее, и Ирану оставлена возможность осуществлять поставки своим ключевым потребителям: Китаю, Японии, Италии и тп.
Мировое производство нефти выросло благодаря США, России и Саудовской Аравии, которые втроем обеспечивают 33% мирового спроса. И это предложение до сих пор компенсировалось ростом спроса со стороны Китая, Индии, Южной Кореи и Японии.
Однако, сейчас складываются предпосылки к перенасыщению рынка. Отраслевые аналитики предупреждают, что ситуация может ухудшиться в связи со все более явными признаками замедления роста мировой экономки.

( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лидеры роста и падения ммвб
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- си
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трейдер
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал
