ЗАВТРА В БОЙ!!!

А многие молодые квикеры-бойцы до сих пор пользуются стандартными индикаторами, машками, болинджерами и параболиками, а некоторые и вообще ничем не пользуются.

И в глазах опытных «охотников» за депозитами:



экипировка молодого бойца выглядят так:


( Читать дальше )

В общем вчера, на встрече КАТ была подана идея сгонять на зимовку в Таиланд.

Идея такая, в середине января по середину Февраля (уточняется) есть возможность поехать на отдых,
снять домик и человек 6-20 (можно парами) можно по одному, пару можно найти на месте (недорого))))




( Читать дальше )

как то уже считал сколько рублей должен стоить бакс
smart-lab.ru/blog/304779.php ... решил пересчитать...

М2/ЗВР = 36487ярд/394ярд= 92руб за бакс

данные брал отсюда 
quote.rbc.ru/macro/indicator/1/181.shtml
www.cbr.ru/hd_base/default.aspx?Prtid=mrrf_m

т.е расхождение достигло 92-64=28руб… это 43%… одно из самых рекордных... 
по графику ситуация напоминает 2013г...

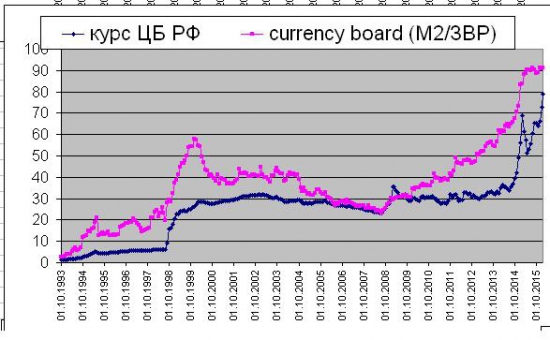
мораль...
имхо надо тарить баксы...
однако звр потихоньку растут

Продолжение. Начало здесь.

Эксперименты

Но как же изменится среднее отклонение оптимизированного портфеля за пределами выборочного контроля, по сравнению с с 1/N? Ниже приведен скрипт для проведения экспериментов с различными структурами портфеля, периодами возврата, ограничениями значений и отклонениями:

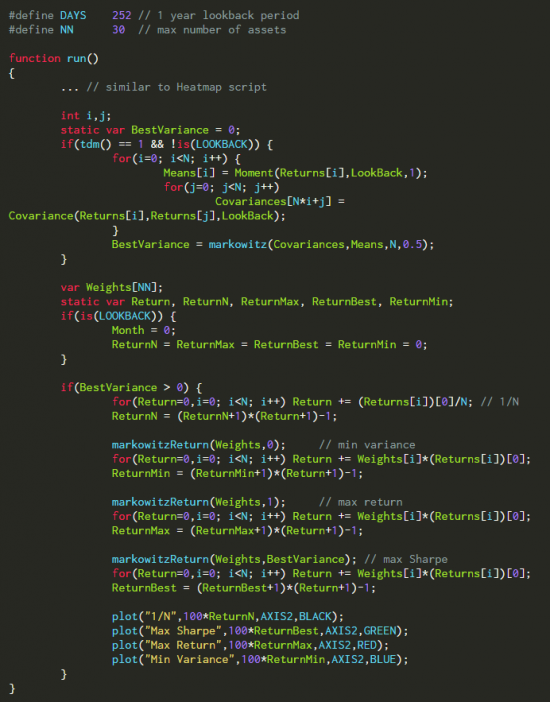
( Читать дальше )

Добрый день!

Для всех QUIKеров в свободное пользование индикатор линейной регрессии (LUA).

Settings = 
{
        Name = "xLinReg",
        period = 128,
        deviation=2,
        line=
        {
                {
                        Name = "xLinReg",
                        Color = RGB(0, 0, 255),
                        Type = TYPE_LINE,
                        Width = 3
                },
                {
                        Name = "xLinReg",
                        Color = RGB(192, 0, 0),
                        Type = TYPE_LINE,
                        Width = 3
                },
                {
                        Name = "xLinReg",
                        Color = RGB(0, 128, 0),
                        Type = TYPE_LINE,
                        Width = 3
                }
        
        }
}



----------------------------------------------------------
----------------------------------------------------------
----------------------------------------------------------
function c_FF()
        
        local AMA={}
        local CC={}
        
        return function(ind, _p,_ddd)
                local period = _p
                local index = ind
                
                local vol = 0
        
                local sigma = 0
                local sigma2 = 0

                local aav = 0
                local bb = 0
                local ZZZ = 0


                                                
                if index == 1 then
                        AMA={}
                        CC={}
                        
                        CC[index]=(C(index)+H(index)+L(index))/3
                        AMA[index]=(C(index)+O(index))/2
                        
                        return nil
                end
                
                ------------------------------
                AMA[index]=AMA[index-1]
                CC[index]=(C(index)+H(index)+L(index))/3
                ---------------------

                if index < (_p) then return nil end
                ----------------------------------------------------
                                
                period =_p
                if index < period then period = index end
        --------------- 
                sigma=0
                sigma2=0
                aav=0
                ZZZ=0
                for i = 0, period-1 do
                        ZZZ=CC[index+i-period+1]
                        aav=aav+ZZZ
                        sigma=sigma+ZZZ*(-(period-1)/2+i)
                        sigma2=sigma2+(-(period-1)/2+i)^2
                end
                
                ------------------------
        bb=sigma/sigma2
        aav=aav/period
                
        AMA[index]=aav+bb*((period-1)/2) ---------линейная регрессия
        -------------------------------
                
                sigma=0
                sigma2=0
                sigma3 = 0
                for i = 0, period-1 do
                        ZZZ=CC[index+i-period+1]
                        sigma2=aav+bb*(-(period-1)/2+i)
                        sigma=sigma+(ZZZ-sigma2)^2

                end
                sigma=(sigma/period)^(1/2)
                
                
                for i = 1, period-1 do
                        ZZZ=aav+bb*(-(period-1)/2+i)
                        SetValue(index+i-period+1, 3, ZZZ)
                        SetValue(index+i-period+1, 2, ZZZ+sigma*_ddd)
                        SetValue(index+i-period+1, 1, ZZZ-sigma*_ddd)

                end     
                        SetValue(index+0-period+1, 3, nil)
                        SetValue(index+0-period+1, 2, nil)
                        SetValue(index+0-period+1, 1, nil)
                
                
                ----------------------------------
                                                                
                        return AMA[index]-sigma*_ddd,AMA[index]+sigma*_ddd, AMA[index]
                        
        end
end
----------------------------    ----------------------------    ----------------------------
----------------------------    ----------------------------    ----------------------------
----------------------------    ----------------------------    ----------------------------

function Init()
        myFF = c_FF()
        
        return 3
end
function OnCalculate(index)
        
        
        
        return myFF(index, Settings.period,Settings.deviation)
        
                
end

Продолжение: http://smart-lab.ru/blog/337978.php

   Добавляю код сделанного мной индикатора Parabolik в котором параметр ускорение зависит от волатильности. Чем больше волатильность, тем больше увеличивается ускорение и индикатор быстрее «догоняет» цену. Подобные есть на просторах интернета для метатрейдера (и не бесплатно), для квика не встречал.

 

Видно, что он дает меньше перескоков (красный), чем обычный Parabolik (черный). Хорошо себя зарекомендовал для выходов из позиций, открытых по тренду. На вход в боковике конечно будет давать ложные сигналы, как и обычный Parabolik (но меньше!), создатель которого не рекомендовал только его использовать для открытия позиций.

Код индикатора:

Settings = {
Name = "Parabolic ATR",
Period_ATR=14,
line = {{
                Name = "Parabolic ATR",
                Type = TYPE_POINT,
                Color = RGB(255,0,0),
                Width = 2
                }
                }
}

old_idx=0
long=false
short=false
revers=false


function Init()
        return 1
end

function OnCalculate(idx)
if idx<Settings.Period_ATR then
return nil
else
if idx==Settings.Period_ATR  then
psar={}
psar[idx]=L(idx)
long=true
hmax=H(idx)
per_ATR=Settings.Period_ATR
local TR=0
for js=(idx-per_ATR),idx-1 do
TR=(TR+H(js)-L(js))
end
Old_ATR=TR/per_ATR
revers=true
else

if idx~=old_idx then
local TR=0
for js=(idx-per_ATR),idx-1 do
TR=(TR+H(js)-L(js))
end
local ATR=TR/per_ATR
af=ATR/(Old_ATR+ATR)
af=af/10
Old_ATR=ATR
if long then
if hmax<H(idx-1) then
hmax=H(idx-1)
end
psar[idx]=psar[idx-1]+af*(hmax-psar[idx-1])
end
if short then
if lmin>L(idx-1) then
lmin=L(idx-1)
end
psar[idx]=psar[idx-1]+af*(lmin-psar[idx-1])
end
revers=true
end
if long and L(idx)<psar[idx] and revers then
psar[idx]=hmax
short=true
long=false
lmin=L(idx)
af=Step
revers=false
end
if short and H(idx)>psar[idx] and revers then
psar[idx]=lmin
long=true
short=false
hmax=H(idx)
af=Step
revers=false
end
end

old_idx=idx

return psar[idx]
end
end

( Читать дальше )

Давно не писал. Лениво.

Вообще дорисовывать свечки, как я в после про ожидаемый рост сбера от 110  smart-lab.ru/blog/315490.php полезно. Программируем рынок)

Честно говоря, направленная торговля опционами на приличный процент ГО съедает нервы несоразмерно доходу. Поза против тебя — ощущение мудака. Поза за тебя — эйфория от роста депо в 2-3 раза такая, что мозг отключается от других дел.

Поэтому, ну его. Сейчас закрыл колы по РТС. Не, не в плюс. Умудрялся закупаться в таких точках, что позавчера по 94100 закрылся в 0.

И вот теперь размышляю о роботизированных опционных стратегиях. И в голову пришёл опционный мартингейл. А что, а вдруг :)

Какая главная проблема мартингейла? Очевидно — накапливаемый убыток по всем позициям и неизбежный конец по маржин колу.

Что дают в мартине опционы. Разумеется только от покупки:

1. ГО купленного опцика всегда ниже ГО базового актива
2. Нельзя потерять больше чем поставил. Например, при традиционном мартине такой шип, как был к примеру на франке после решения ЦБ сразу убивает. Ещё и должен останешься. Опционный мартин теряет только те фишки, которые уже на столе.
3. +dx > -dx, — с виду идиотская формула. Но имеется ввиду то, что по классике, БА пошёл на x, x у тебя в кармане. Пошёл на минус x, х** у тебя в кармане, а по доходу минус x.
   А в опционе движение БА даёт разные прибавки. Например, опцик стоит 500. БА минус 5000 — опцик стоит 50. БА плюс 5000 — опцик стоит 2400.

Разумеется, платим за эту красоту мы теттой. Безжалостной и беспощадной.

Что думают господа опытные опционщики про это.

Решил копнуть чуть глубже в ARIMA и другие подобные модели. Попробовал предсказывать цену, а точнее, диапазон цен на ближайшую минуту и 5 минут и на этом сделать какие-то деньги. И что интересно, получилось. Хотя, возможно, это случайность отчасти, не тестировал на большом горизонте времени.

В комментариях к коду все есть.

ARIMA (англ. autoregressive integrated moving average, иногда модель Бокса — Дженкинса, методология Бокса — Дженкинса) — интегрированная модель авторегрессии — скользящего среднего — модель и методология анализа временных рядов. 

Основная идея этой модели в том, что цена в будущем зависит от цен в прошлом (авторегрессионная часть AR) и возврата к среднему (MA часть). А интегрированность означает то, что предварительно определяется порядок интегрированности для временного ряда. К примеру, порядок 1 означает, что разности 1 порядка являются стационарными. Для самой цены порядок интегрированности должен получаться равным 1, а для доходностей — 0. 

( Читать дальше )

Окей, 100 плюсов есть. Обещанный способ угадывания гэпа.

Идем к сайлентбобу: smart-lab.ru/blog/206454.php
Что видим:
1) только лонг
2) работает с 2011 года, до этого времени нет
3) сделок с весны 2011 до сентября 2014 мало — 123 штуки — событие с одной стороны редкое, а с другой вполне себе равномерно распределено по году (смотрим эквити). Процент выигрыша 65, профит фактор 2,77.
4) паттерн достаточно очевидный чтобы его было не жалко отдать сматрлабовцам.

Какое у нас редкое равномерно распределенное очевидное событие? День недели. Строим простейший скрипт и смотрим есть ли закономерности в Си по дням недели.

Чего видим? в пятницу у нас гэп скорее вверх, причем профит фактор сразу 2,56. Смотрим на эквити:

 

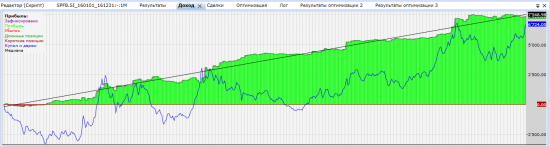
Все красиво, похоже предположение верное. На следующем шаге добавляем фильтр в стиле «на момент входа снизились не более чем на определенную величину от закрытия предыдущего дня». Часть сделок отсеиваем, улучшаем ПФ на 0,39. Радуемся, исследуем дальше, встраиваем в свои системы.


А заодно начинаем думать почему так может происходить, и почему до 2011 было по-другому. До мая 2010 пятничный гэп в целом повторял движение самого Си, а с мая 2010 до начала 2011

( Читать дальше )