Не случайно, когда мы видим на своих фильтрах большие проторгованные объемы на опционах, это приводит к большим движениям на акциях за короткий промежуток времени. Имея эту информацию, у вас будет хорошее преимущество. Давайте рассмотрим почему?

Для каждого купленного опциона есть проданный, иными словами это антагонистическая игра (если заработал прибыль, то кто-то потерял такую же сумму). Чаще крупными продавцами опционов (кол/пут) являются брокерские дилеры и маркет-мейкеры, которые выставляют большие блоки опционов по цене аск.

Одна из причин, почему происходят такие большие движения в акциях, является то, что при продаже опциона «колл» крупный дилер должен захеджировать свой опцион через покупку акций. Это может привести к увеличению объема покупок и привести к большим движениям в акции.

Т.к. акция растет и дельта проданного опциона кол тоже подрастет, то дилеры, которые до этого идеально захеджировали опцион по дельте вынуждены покупать еще акции, т.к. дельта по «проданному колу» изменилась.

( Читать дальше )

запись вэбинара

Вчера немного рассказал про свой подход к опционным улыбкам. 
Приходите на опционную конференцию 9 апреля, продолжим разговор.

Посчитал на R спред между акциями Google и Apple с учётом соотношения (hedge ratio). И нанёс среднюю линию с двумя среднеквадратичными отклонениями сверху и снизу. Красота. 



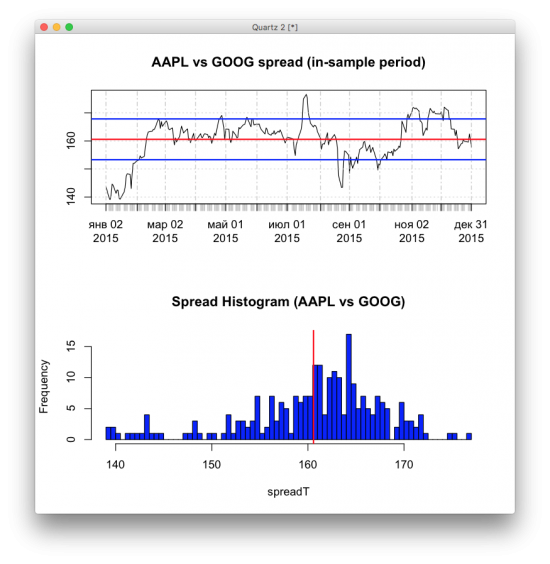
Делается на R это очень просто, код ниже. 

require(quantmod)
> startT <- «2015-01-01»
> endT <- «2016-01-01»
> rangeT <- paste(startT, "::", endT, sep="")
> symbols <- c(«AAPL», «GOOG»)
> getSymbols(symbols)
[1] «AAPL» «GOOG»
> tGOOG <- GOOG[,6][rangeT]
> pdtGOOG <- diff(tGOOG)[-1]
> tAAPL <- AAPL[,6][rangeT]
> pdtAAPL <- diff(tAAPL)[-1]
> model <- lm(pdtAAPL ~ pdtGOOG)
> hr <- as.numeric(model$coefficients[1])
> spreadT <- tAAPL — hr * tGOOG
> meanT <- as.numeric(mean(spreadT, na.rm=TRUE))
> sdT <- as.numeric(sd(spreadT, na.rm=TRUE))
> par(mfrow = c(2,1))
> hist(spreadT, col=«blue», breaks = 100, main = «Spread Histogram (AAPL vs GOOG)»)
> plot(spreadT, main=«AAPL vs GOOG spread (in-sample period)»)
> abline(h = meanT, col = «red», lwd = 2)
> abline(h = meanT + 1 * sdT, col = «blue», lwd = 2)
> abline(h = meanT — 1 * sdT, col = «blue», lwd = 2)

Здесь: 

meanT — среднее
sdT — среднекв. отклонение
spreadT — спред
par — график с двумя секциями
plot — график
hist — гистограмма
abline — линия поверх графика
model — линейная зависимость модель, МНК
quantmod — библиотека для получения исторических данных
rangeT — временной диапазон

Хотите попросить сделать количественный анализ чего-нибудь? Пишите в личку или в комментариях.

По ФА…

На уходящей неделе:

Выступления членов ФРС

В отличие от заседания ФРС 16 марта риторика членов ФРС на уходящей неделе была ястребиной.
Чарльз Эванс заявил, что ожидает в этом году двукратное повышение ставки в случае, если рост экономики и инфляции в США не будет существенно превышать прогнозы.
Комментируя текущие прогнозы относительно планируемой траектории повышения ставок ФРС, Эванс признался, что его прогнозы всегда были «на нижней стороне», но сейчас он согласен с большинством членов ФРС относительно прогнозов по повышению ставок.
Эванс является вечным голубем ФРС и подобное заявление говорит о том, что прогнозы ФРС по повышению ставки сейчас наиболее реалистичны.

( Читать дальше )

внимание! возможно Грааль! возможно рабочий! так как нет времени его проверять — занят инным граальчиком -попробует может кто и напишет резалт за неделю. за грааль спасибо не надо — просто напишите сколько принес грааль  за неделю или что я — м… ак (если не принесет ничего)))

итак.

берем инструиент ликвидный по опционам чтоб был — например Si или RTS или… кто на америке или англии там наверное ES или EuroUSD подойдут.

стакан открываем опциона со страйками прилично отдаленными от текущей цены базы

смотрим достаточна ли там ликвидность и спред чтоб адекватный и сама премия близка к теоретической.
далее.

с помощью калькулятора Пивот уровни Тома ДеМарка (можно вот тут вбить OHLC  : http://extra.agea.com/ru/tools-ru/calculators/pivot-levels-ru/demarks-pivot-points-ru   )
находим предполагаемые границы завтрашнего диапозона дня — там минимум и максимум рассчитывается исходя из цен откр, закр, хай/лоу вшерашнего дня/периода -например для рубля с учетом ночного закрытия рынка и корреляции его с нефтеценами на брент я бы учитывал что открытие рубля не всегда точно отображает то что за ночь было в нефти. а так как рубль привязан к нефти то скорректируйте (это надо минут 10 потратить) цену предпологаемого вчерашнеторгового открытия дня относительно нефти -хотя это не обязательно — итак можно просто OHLC вчерашнего рубля вставить -уровни все равно не попадут всегда точно, но нам и не нужно точность — нам нужно примерно предпологать где будет макс/мин завтра на рынке.

( Читать дальше )

1. 16.03.2016  Экспортерам «разрешили» не продавать валюту. 
«Корпорации не спешат расставаться с долларами и евро, предпочитая расплачиваться с государством рублевыми кредитами, объясняют аналитики.
«Большую часть остальных налоговых выплат экспортеры, вероятно, профинансируют за счет заимствований в ЦБ — по нашим оценкам, на сумму около 250-300 млрд рублей»

2. 15.03.2016 ЦБ выделил 230 млрд рублей дополнительных кредитов через основную операцию рефинансирования — недельное репо, лимит по которому был повышен до рекордных за полтора месяца 670 млрд рублей.
Решение ЦБ можно считать неожиданным, следует из комментариев Райффайзенбанка и «Уралсиб Кэпитал».Решение же нарастить предложение рублей в условиях, когда ликвидность и так и избытке, создает новые риски для рубля, поскольку полученные кредиты могут быть использованы для покупки долларов…

( Читать дальше )

Если мы хотим строить прибыльные торговые системы, то надо понимать – случайны ли цены на рынке и или нет, есть ли разница между случайным блужданием и движением цены и в чем оно состоит?

Для более подробного изучения этого вопроса решил быстренько написать небольшую программу и визуально проанализировать.

На графике верхняя и средняя область (а нижний объем) — это свечные графики цены по ES. Один из них построен по реальным ценам, второй по случайным значениям. Как думаете какой из них реальный и почему?

Подумали? Вот ответ, на верхнем — реальные цены, а на среднем — случайное блуждание. На сколько они схожи или отличаются и в чем? Прошу высказываться! ;)

 

Для желающих «побаловаться» и покопаться поглубже предлагаю скачать мою программку вот тут https://cloud.mail.ru/public/35qz/rAuePAS63 (вирусов нет). Для работы требует .net 4.5 у кого нет могут установить от сюда 

( Читать дальше )

Начало здесь.

Зависит ли корреляция сигналов от оборачиваемости?

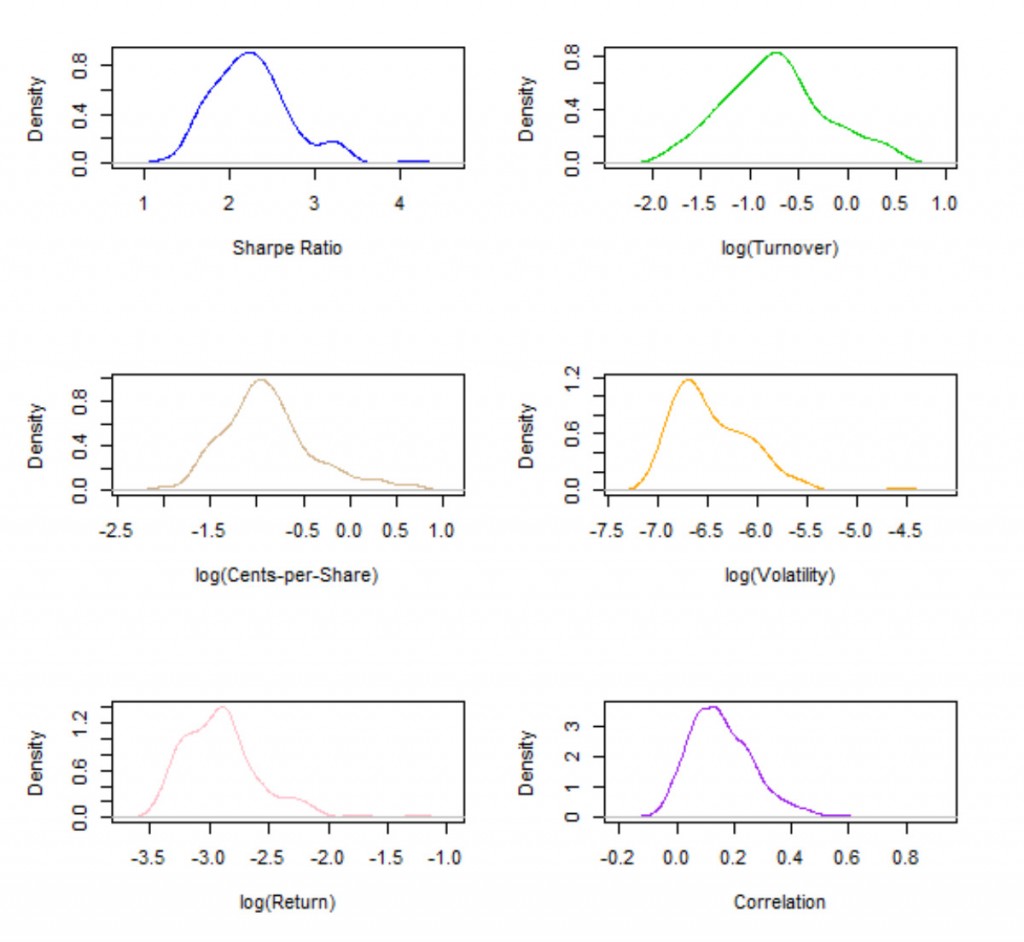
Если мы проведем параллель между сигналами и акциями, то оборачиваемость по каждому альфа-сигналу является аналогом ликвидности акций, которая обычно измеряется через средний дневной объем торгов (ADDV). Логарифм ADDV обычно используется  как фактор риска в многофакторных моделях для аппроксимации ковариации матричной структуры портфеля ценных бумаг, чье назначение заключается в моделировании вне-диагональных элементов ковариационной матрицы, то есть структуры парных корреляций. Следуя этой аналогии, мы можем задать вопрос, может ли оборачиваемость – или точнее ее логарифм – объяснить  корреляции альфа-сигналов? Очевидно, что примененение оборачиваемости напрямую (в отличие от логарифма) ничего не даст из-за чрезвычайно искаженного (грубо логарифмически нормального) распределения оборота (см. рисунок в заглавии).

( Читать дальше )

Сделал на R такую красоту ) В общем, вывод такой: нефть за 5 минут чаще всего ходит на 0-20 центов. Очень редко на 40 центов. Зная это, можно стоп ставить где-то на 20 центах от лоя свечи, где зашел. Если стоп сняли, значит, лонганул рано )

И кстати видно на глаз, что доходности подчиняются нормальному распределению.. А значит, сама цена на нефть — лог-нормальному. 
Еще видно, что за 5 минут расчитывать больше чем на 20 центов не стоит. И можно с высокой вероятностью жадно пипсануть 5 центов )



Напишите, что еще хотели бы узнать, чтобы я посчитал на R? 

Если хотите меня нанять количественным аналитиком (квантом), милости прошу, пишите в личку )