Блог им. fxsaber
Алгоритмическая или реальная Оптимизация?
- 16 апреля 2024, 01:25
- |
Для ускорения оптимизации ТС делают следующее
- Увеличивают количество параллельных вычислительных потоков.
- Пробуют разные компиляторы.
- Переписывают код под особенности железа (OpenCL, GPU и т.д.).
- Пробуют разные алгоритмы оптимизации.
- Уменьшают количество входных данных (цены, календарь и т.д.).
- Заменяют внутренние алгоритмы на более оптимальные по вычислительным ресурсам.
Последний пункт называют алгоритмической оптимизацией.
Реальная оптимизация.
А может ли реальная (вычислительная) оптимизация ускорить оптимизацию? Звучит, как масло масленное.
Ниже приведу пример, который, возможно, кого-то натолкнет на полезные идеи ускорения расчетов в своих ТС.
Пример.
Хотелось привести не гипотетический, а реальный пример, но при этом лаконичный. И тут случай подвернулся.
Разбирался с особенностями DST/GMT-смещений в разных источниках котировок и календаря. Там многое завязано на первом/втором/последнем воскресенье месяца. Поэтому ядром подобных вычислений является расчет времени начала месяца. Вот эту функцию и попробуем ускорить.
datetime GetMonthTime( const int Year, const int Month )
{
const MqlDateTime time = {Year, Month, 1};
return(StructToTime(time));
}
Казалось бы, что тут ускорять? А главное — как?!
Оптимизация — кто кому служит?
Чем меньше математических действий, тем быстрее работает алгоритм. Поэтому немного включив интуицию, напишем общий вид функции, который хотим получить.
#define DAY (24 * 3600)
datetime GetMonthTime2( const int Year, const int Month )
{
// Количество дней от начала года до начала месяца: январь - 0, февраль - 31, март - 59, ...
static const double Months[] = {0, 0, 31, 59, 90, 120, 151, 181, 212 ,243, 273, 304, 334};
return((datetime)(((Year - 1970) * inKoef1 + Months[Month] * inKoef2) * DAY) / DAY * DAY);
}Код родился из следующих соображений. Раз есть год и месяц на входе, то почему бы не ограничиться по одному коэффициенту на каждый входной.
Коэффициенты.
А вот подобрать эти коэффициенты способна стандартная оптимизация. Поэтому пишем ФФ (фитнесс функцию) и натравливаем оптимизатор.
input double inKoef1 = 365;
input double inKoef2 = 1;
sinput int inYearFrom = 1970;
sinput int inYearTo = 2099;
input int inMonth = 1;
double OnTester()
{
double Sum = 0;
for (int i = inYearFrom; i <= inYearTo; i++)
Sum -= (double)MathAbs(GetMonthTime(i, inMonth) - GetMonthTime2(i, inMonth));
return(Sum);
}
Для наглядности, в качестве оптимизатора выступит многоядерный MT5-Тестер в режиме математических вычислений.
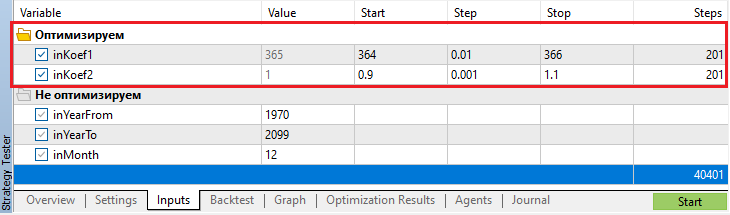
Запускаем и мгновенно получаем результат.
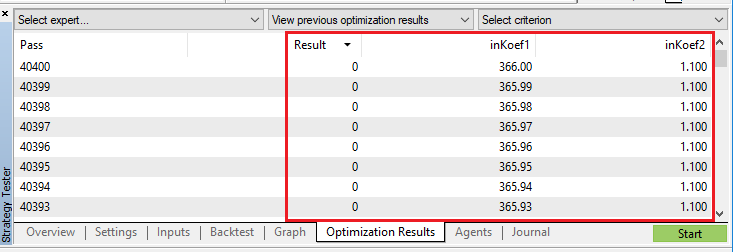
Нулевая ошибка (полное совпадение с тем, что надо получить) и комбинации соответствующих коэффициентов.
Делаем так для каждого месяца. И в итоге получаем искомую функцию.
// Работает до конца XXI-века.
datetime GetMonthTime3( const int Year, const int Month )
{
static const double Months[] = {0, 0.45, 31 * 1.01, 59 * 1.01, 90 * 1.007, 120 * 1.005, 151 * 1.004, 181 * 1.004,
212 * 1.003, 243 * 1.003, 273 * 1.002, 304 * 1.002, 334 * 1.002};
return((datetime)(((Year - 1970) * 365.25 + Months[Month]) * DAY) / DAY * DAY);
}
Ускорение.
Выглядит некрасиво, но работает в 10-20 раз быстрее исходной!
Наверное, подобная по скорости функция где-то опубликована. Но сгодилась в качестве примера механизма ускорения.
теги блога fxsaber
- HFT
- Meta Trader 4
- Meta Trader 5
- MetaQuotes
- Metatrader
- Metatrader 4
- MetaTrader 5
- MetaTrader5
- mql
- mql5
- mt4
- mt5
- MT5 MQL5
- OOS
- tslab
- адаптивность
- алготрейдинг
- анализ торговли
- белый лебедь
- бэктестинг
- Грааль
- даркпулы
- децентрализованная биржа
- диверсификация
- диверсификация портфеля
- доходность
- драйвер
- ДЦ форекс
- железо
- задержки
- закономерности рынка
- закономерность
- издержки
- инвестиции
- инвестор
- исполнение ордеров
- исследование
- итоги
- итоги месяца
- Калькулятор
- комиссия
- комиссия брокера
- криптовалюта
- Лебедь
- лебедь черный
- лимитные ордера
- лучший памм счет
- лчи
- максимальная просадка
- Маркетинг
- машинное обучение
- метатрейдер
- миф
- мониторинг
- мониторинг счета
- нейронные сети
- Нейросети
- оборот торгов
- операционная система
- оптимизация роботов
- Оптимизация торговой системы
- Отчет о торговле
- ПАММ
- памм счета инвестиции
- переворот
- портфель
- проверка системы
- продажи
- просадка
- проскальзывание
- результат торговли
- рейтинг
- робот
- Сверхприбыли
- сверхприбыль
- свопы
- Скальпинг
- спред
- статистика
- статья
- стейтмент
- Телеграм
- телеграмм канал
- тестер
- тестер МТ5
- тики
- тики. работа с хистори
- тиковая история
- торговая система
- торговые роботы
- торговые системы
- трагедия
- трейдинг
- тренд
- фильтр
- фильтрация
- форекс
- хедж-фонд
- чёрный лебедь
- шторм



















Что касается самой задачи оптимизации для алго, то просто для затравки перечислю последовательность задач и методов.
1. Самое неформальное и сложное, это выбор функционала, который нужно оптимизировать. Как-то доходность, Шарп, Сортино, список на самом деле обширный. Некоторые вообще отказываются от сведения задачи к функционалу и воюют с многомерной оптимизацией.
2. Собственно алгоритмы оптимизации. Перечислены в любом учебнике.
Перебор по сетке. Покоординатный спуск. Сопряженные градиенты. Метод Ньютона и численные его вариации. Метод ветвей и границ. Монте-Карло. Генетика.
3. Переподгонка и что с ней делать или можно ли делать то, что нельзя. А если можно, то как.
SergeyJu, В моем текущем подходе нет понятия «оптимизация» и какого-то процесса, похожего, на то, что алго-трейдеры под ней понимают. Но было время, когда что-то похожее у меня было. Но даже если я перемещусь в то время, даже из него всё это для меня выглядит не очень историей. Причем и (1) и (2), ну (3) — классика, тут без вариантов).
При оптимизации, если такой процесс есть, нужно оптимизировать робастность. Ну или робастность и какую-то метрику качества. Даааже если ты выбрал какую-то метрику про робастность, смотреть надо не на метрику прогона, а на метрики прогонов — и не для того чтобы найти у кого больше.
Алгоритмы оптимизации — ну раз тумбочка из под ног пункта 1 выбита, из под 2 автоматом тоже вылетает.
(3) — как сказал, бессмертная классика.
Часто оптимизация маскируется под что-то другое. Например, выбор таймфрейма или актива.
С робастностью (устойчивостью, грубостью) тоже не все просто.
Если в некоторой области значений все получаемые системы вполне себе торгуемы и можно торговать не одну систему, а пучок — наблюдается некая робастность.
Но ни откуда не следует, что, в силу нестационарности цен, эта зона в будущем не престанет нести деньги робастно-робастно.
Не, ну как тип задачи, что-то есть конечно, но оно оочень отличается от вот этой истории с прогонами подобного.
Ну мож я сам тут конечно, слишком сильно деклассировал подход), но вот алгоритмы из (2) — они же, вроде, не особо ищут какие-то плато или точки стабильности — им просто нужен максимум — глобальный или локальный.
Если анализировать группы результатов не только как способ найти «самого здорового», то конечно в этом будет на порядок больше смысла.
Одно время я баловался с критериями типа хи-квадрат, Акаике и так далее. Но те грубости, в который мы копаемся, весьма далеки от красивостей матстатистики. Что ни говори, высокий уровень шума и нестационарность
«с белой ручки не стряхнешь и за пояс не заткнешь».