SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. AlexSwan
Оценка возможной просадки при работе постоянным лотом
- 15 февраля 2013, 11:14
- |
У нас есть некоторая система, торгуется постоянным лотом.
Мы протестировали систему на истории с лотом равным 1, и посчитали её характеристики:
A — размер средней положительной сделки, B — размер средней отрицательной, P — вероятность положительной сделки,
и Q=1-P — вероятность отрицательной сделки.
Вопрос: Какую просадку может дать такая система при дальнейшей торговли тем же лотом равным 1?
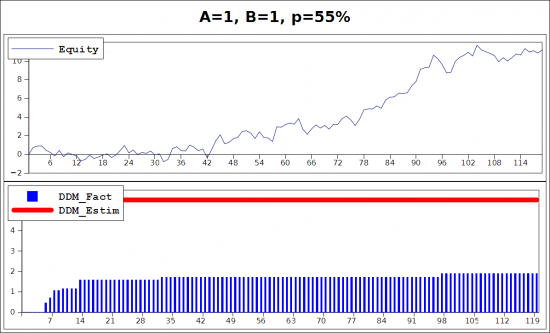
С довольно большой вероятностью (около 99%) просадка с момента старта системы не будет превышать величину
DDM_Estim = 2.25*(A+B)^2*P*Q/(AP-BQ)
Разумеется, эта оценка работает только в случае положительного среднего системы.
На картинках нарисована немного другая ситуация, просадка измеряется не с момента старта, а постоянно в каждой точке.
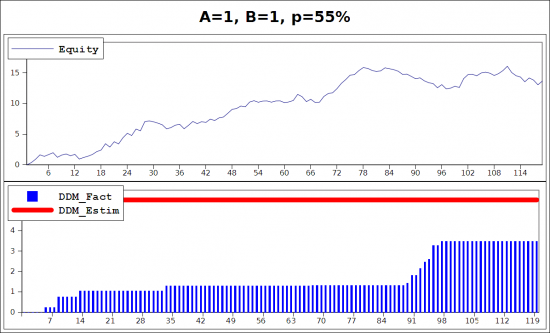
На картинках нарисована немного другая ситуация, просадка измеряется не с момента старта, а постоянно в каждой точке.
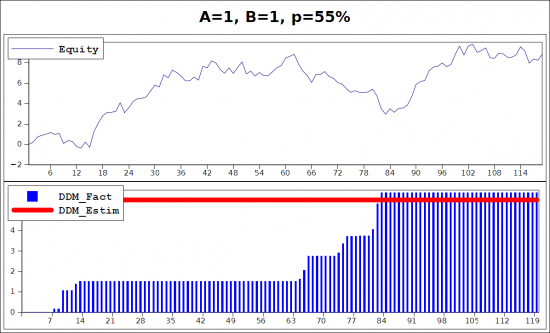
А вот и случай превышения фактической просадки над оценкой:
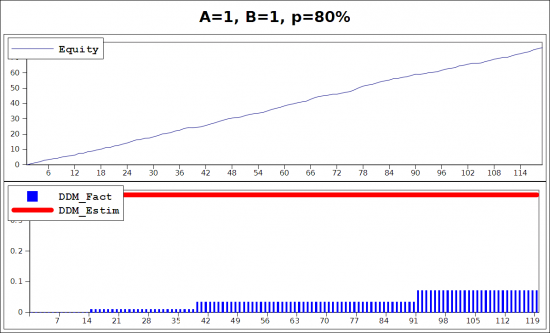
И ещё одна картинка, с большим положительным средним:
Оригинал: swantrade.livejournal.com/29744.html
Мы протестировали систему на истории с лотом равным 1, и посчитали её характеристики:
A — размер средней положительной сделки, B — размер средней отрицательной, P — вероятность положительной сделки,
и Q=1-P — вероятность отрицательной сделки.
Вопрос: Какую просадку может дать такая система при дальнейшей торговли тем же лотом равным 1?

С довольно большой вероятностью (около 99%) просадка с момента старта системы не будет превышать величину
DDM_Estim = 2.25*(A+B)^2*P*Q/(AP-BQ)
Разумеется, эта оценка работает только в случае положительного среднего системы.
На картинках нарисована немного другая ситуация, просадка измеряется не с момента старта, а постоянно в каждой точке.

На картинках нарисована немного другая ситуация, просадка измеряется не с момента старта, а постоянно в каждой точке.
А вот и случай превышения фактической просадки над оценкой:

И ещё одна картинка, с большим положительным средним:

Оригинал: swantrade.livejournal.com/29744.html
теги блога Swan
- Brent
- ETF
- forex
- Gold
- Light
- Ri
- Si
- SnP
- август 2013
- анализ рынка
- арбитраж
- биржа
- Блэк-Шоулз
- боковик
- волатильность
- выборы
- вью
- Грааль
- дисциплина
- доллар-рубль
- Золото
- игра
- История
- итоги
- кино
- книга
- Книги
- Книги по трейдингу
- ЛЧИ 2012
- математика
- ММ
- модели
- Моя торговля
- моя торговля за неделю
- нефть
- обучение
- Одураченные случайностью
- опцион
- опционы
- оффтоп
- Парный трейдинг
- ПИФ
- портфель
- прогноз
- прогнозирование
- просадка
- работа
- работа над ошибками
- рабочее место
- рабочее место трейдера
- рабочее пространство
- результаты
- реинвест
- рецензия
- рецензия на книгу
- Ри
- Риски
- ротшильд
- РТС
- рынок
- Рынок - взгляд
- рынок - взгляд
- сигнал
- система
- Система биржевой торговли
- система торговли
- системная торговля
- спайки
- статистика
- стопы
- стратегии
- стратегия
- Талеб
- Талеб Насим
- теория
- технический анализ
- тильт
- торговая система
- торговая стратегия
- торговая тактика
- торговля
- торговля на новостях
- торговля онлайн
- трейдинг
- тренды
- удача
- управление активами
- Управление капиталом
- управление позицией
- управление рисками
- фильм
- фильм для трейдера
- фильмы
- флэт
- фонды
- форекс
- Фракталы
- Черный Лебедь
- экспирация март 2012



















(1-D/L)^(2*Q-1),
где L — стартовый рычаг на начало торговли, Q — коэффициент Шарпа, рассчитанный по периодическим доходностям эквити