SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. AlexeyPetrushin
Gaussian Mixture vs Generalised Hyperbolic, Прогноз Цены Акций
- 13 января 2025, 13:38
- |
Апроксимация Распределения Вероятностей цен MSFT за 360, 180 и 30 дней.
Явно видно что Нормальный Микс из 3х компонент намного лучше повторяет форму распределения чем Обобщенная Гиперболическая Модель.
Проблемы:
— Непонятно как менять его волатильность? В нормальном мы меняем сигму — и распределение меняется, а здесь 3 компоненты, у каждого своя сигма и среднее. Если есть идеи как маштабировать полученный нормальный микс было бы интересно услышать.
— Лучшее совпадение не значит что это лучше, это может быть оверфиттинг.
Маштабирование:
Нужно для настройки модели на текущую волатильность. Скажем мы на истории за десятки лет определили общую форму Нормального Микса для MSFT как меняются акции за 1 мес. Но, нам ведь интересно затем настроить (маштабировать) эту общую форму на текущую волатильность MSFT, отмаштабировав общую форму, на текущую волатильность MSFT за последний месяц. Непонятно как это сделать.
Зачем это нужно:
Знать будущее распределение цен (у нас правда не будущее, а прошлое, которое мы за неимением лучшего используем как будущее) — может быть полезно для моделирования различных сценариев и подбора гиперпараметров, расчета цен опционов, формирования оптимального по тому или иному критерию портфеля, симуляция стресс теста, расчет цен опционов, и т.п.
Графики
Зеленый положительные изменения, красный отрицательные. Эмпирическое распределение самое яркое, Гиперболическое чуть легче цвета, Гауссовский Микс самый легкий цвет. Каждый график в двух маштабах, линейном и логарифмическом.
MSFT 360d

MSFT 180d

NEM 30d, компания с серией огромных убытков, огромный красный хвост, и Гауссовский Микс смог его захватить
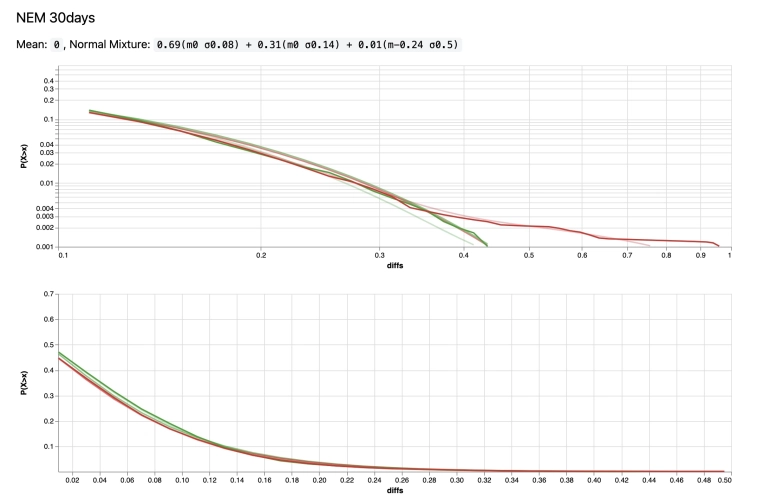
Данные:
Явно видно что Нормальный Микс из 3х компонент намного лучше повторяет форму распределения чем Обобщенная Гиперболическая Модель.
Проблемы:
— Непонятно как менять его волатильность? В нормальном мы меняем сигму — и распределение меняется, а здесь 3 компоненты, у каждого своя сигма и среднее. Если есть идеи как маштабировать полученный нормальный микс было бы интересно услышать.
— Лучшее совпадение не значит что это лучше, это может быть оверфиттинг.
Маштабирование:
Нужно для настройки модели на текущую волатильность. Скажем мы на истории за десятки лет определили общую форму Нормального Микса для MSFT как меняются акции за 1 мес. Но, нам ведь интересно затем настроить (маштабировать) эту общую форму на текущую волатильность MSFT, отмаштабировав общую форму, на текущую волатильность MSFT за последний месяц. Непонятно как это сделать.
Зачем это нужно:
Знать будущее распределение цен (у нас правда не будущее, а прошлое, которое мы за неимением лучшего используем как будущее) — может быть полезно для моделирования различных сценариев и подбора гиперпараметров, расчета цен опционов, формирования оптимального по тому или иному критерию портфеля, симуляция стресс теста, расчет цен опционов, и т.п.
Графики
Зеленый положительные изменения, красный отрицательные. Эмпирическое распределение самое яркое, Гиперболическое чуть легче цвета, Гауссовский Микс самый легкий цвет. Каждый график в двух маштабах, линейном и логарифмическом.
MSFT 360d

MSFT 180d

NEM 30d, компания с серией огромных убытков, огромный красный хвост, и Гауссовский Микс смог его захватить

Данные:
duration = [360, 180, 30]
diffs = log(price_i/price_{i-duration})теги блога Alex Craft
- amd
- java
- Javascript
- microsoft
- portfolio
- python
- swift
- Uranium One
- usd
- акции
- алгоритм
- алготрейдинг
- анализ
- аналитика
- банки
- Беларусь
- бизнес
- Брокер
- брокеры
- валюта
- волатильность
- госдолг США
- данные
- деньги
- доллар
- доллар рубль
- игра
- ИИ
- иммиграция
- инвестирование
- инвестиции
- инсайдер
- инфляция
- инфляция в России
- инфляция в США
- искусственный интеллект
- исторические данные
- Келли
- макро
- макроэкономика
- Мандельброт
- математика
- мобильный пост
- модели
- модель
- монте-карло
- мудрость
- недвижимость
- Нелинейность рынка
- неопределенность
- Нефть
- Новости
- оптимальный портфель
- оптимизация
- опцион
- опционы
- отчёт
- оффтоп
- парето
- перевод
- перевод денег
- плечи
- политика
- портфель
- портфолио
- премиальные опционы
- прибыль
- прогноз
- программироание
- пут опцион
- пут опционы
- распределение
- Ребалансировка
- ресурсы
- рецензия на книгу
- риск
- робот
- рост
- рубль
- рынки
- рынок
- спекуляции
- статисика
- статистика
- стратегии
- США
- теория вероятностей
- теханализ
- торговые роботы
- трейдинг
- уран
- философия
- форекс
- фрактал
- фракталы
- хэдж
- шортсквиз
- экономика
- экономика США
- энергия



















Не бойтесь оверфитинга — есть формальные тесты, которые позволяют сравнить две оценки в которых разное количество параметров
en.wikipedia.org/wiki/Likelihood-ratio_test
С произвольно гуляющими средними слишком непонятно получается, теряется понятие сигмы как меры волатильности
Возможно Гиперболическое может быть интересно если нужна аналитическая форма распределения, но мне она не нужна, я использую численные методы и симуляции, и с Гауссовским Миксом работать проще, интуитивно понятней, и аппроксимирует он не хуже.