SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. Artyom_KO
Парадокс Монти Холла (Помогите разрешить спор)
- 22 апреля 2014, 08:30
- |
НАчал читать Булашева «Статистика для трейдеров»
И как водится кроме самой книги начал гуглить всякую всячину и кое что было для меня полезным и интересным
в частности www.natalymath.ru/index.html очень рекомендую, для тех кто далек от тервера и мат статистики или успел все забыть с университета, рекомендую.
Вернемся к теме...
Наткнулся в числе прочего вот на такой парадокс. http://ru.wikipedia.org/wiki/%CF%E0%F0%E0%E4%EE%EA%F1_%CC%EE%ED%F2%E8_%D5%EE%EB%EB%E0
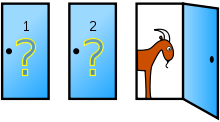
Задача формулируется как описание игры, основанной на американском телешоу «Let’s Make a Deal», и названа в честь ведущего этой передачи. Наиболее распространённая формулировка этой задачи, опубликованная в 1990 годув журнале
Parade Magazine, звучит следующим образом:
Наиболее популярной является задача с дополнительным условием № 6 из таблицы — участнику игры заранее известны следующие правила:
При решении этой задачи обычно рассуждают примерно так: ведущий всегда в итоге убирает одну проигрышную дверь, и тогда вероятности появления автомобиля за двумя не открытыми становятся равны ½, вне зависимости от первоначального выбора. Но это неверно.
Вся суть в том, что своим первоначальным выбором участник делит двери: выбранная A и две другие — B и C. Вероятность того, что автомобиль находится за выбранной дверью = ⅓, того, что за другими = 2⁄3.
Для каждой из оставшихся дверей вероятность выигрыша в сложившейся ситуации вычисляется так:


Где ½ — условная вероятность нахождения автомобиля именно за данной дверью при условии, что автомобиль не за дверью, выбранной игроком.
Ведущий, открывая одну из оставшихся дверей, всегда проигрышную, сообщает тем самым игроку ровно 1 бит информации и меняет условные вероятности для B и C соответственно на «1» и «0».
После этого действия выражения принимают вид:

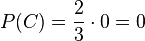
Таким образом, участнику следует изменить свой первоначальный выбор — в этом случае вероятность его выигрыша будет равна 2⁄3.
Одним из простейших объяснений является следующее: если вы меняете дверь после действий ведущего, то вы выигрываете, если изначально выбрали проигрышную дверь (тогда ведущий откроет вторую проигрышную и вам останется поменять свой выбор чтобы победить). А изначально выбрать проигрышную дверь можно 2 способами (вероятность 2⁄3), то есть если вы меняете дверь, вы выигрываете с вероятностью 2⁄3.
Этот вывод противоречит интуитивному восприятию ситуации большинством людей, поэтому описанная задача и называется парадоксом Монти Холла, то есть парадоксом в бытовом смысле.
А интуитивное восприятие таково: открывая дверь с козой, ведущий ставит перед игроком новую задачу, как бы никак не связанную с предыдущим выбором — ведь коза за открытой дверью окажется независимо от того, выбрал игрок перед этим козу или автомобиль. После того, как третья дверь открыта, игроку предстоит сделать выбор заново — и выбрать либо ту же дверь, которую он выбрал раньше, либо другую. То есть, при этом он не меняет свой предыдущий выбор, а делает новый. Математическое же решение рассматривает две последовательные задачи ведущего, как связанные друг с другом.
Однако следует брать во внимание тот фактор из условия, что ведущий откроет дверь с козой именно из двух оставшихся, а не дверь, выбранную игроком. Следовательно, оставшаяся дверь имеет больше шансов на автомобиль, так как она не была выбрана ведущим. Если рассмотреть тот случай, когда ведущий, зная, что за выбранной игроком дверью находится коза, все же откроет эту дверь, этим самым он нарочно уменьшит шансы игрока выбрать правильную дверь, так как вероятность правильного выбора будет уже ½. Но подобного рода игра будет уже по другим правилам.
Дадим ещё одно объяснение. Предположим, что вы играете по описанной выше системе, то есть из двух оставшихся дверей вы всегда выбираете дверь, отличную от вашего первоначального выбора. В каком случае вы проиграете? Проигрыш наступит тогда, и только тогда, когда с самого начала вы выбрали дверь, за которой находится автомобиль, ибо впоследствии вы неизбежно перемените свое решение в пользу двери с козой, во всех остальных случаях вы выиграете, то есть, если с самого начала ошиблись с выбором двери. Но вероятность с самого начала выбрать дверь с козой 2⁄3, вот и получается, что для победы нужна ошибка, вероятность которой в два раза больше правильного выбора.
Еще более наглядное объяснение можно дать, если представить что дверей не 3 а, скажем 1000, и после выбора игрока ведущий убирает 998 лишних, оставляя 2 двери: ту которую выбрал игрок и еще одну. Очевидно, что вероятность нахождения приза за каждой из них вовсе не ½. Гораздо большая вероятность его нахождения, а именно 0.999, будет иметь место при смене решения и выборе двери отобранной из 999. В случае с 3 дверьми логика сохраняется, но вероятность выигрыша при смене решения ниже, а именно 2⁄3.
Так вот поделившись данной статьей со своим другом и своими умозаключениями разразился спор в короый было вовлечено еще человек 6 )))
Суть спора заключается в том, что реален ли этот парадокс? Действительно ли выгодно менять мнение? Или нет ни какой разницы?
Не хочу признаваться в числе кого нахожусь, я ))) Но я в меньшинстве)))) 2 к 7 )))) Я не твердолобый, в том смысле что я действительно хочу разобраться и если я не прав, то с легкостью приму реальность....
Основная аргументация одних, это то, что «вероятность не имеет памяти» примеры с бросанием монетки (вероятность выпадения орла или решки всегда остатся 50% независимо от того что выпало ранее)
Других собственно сама статья в википедии с математическим расчетом и видео с передачи «Разрушители легенд» которое подтвержает данную теорию
И как водится кроме самой книги начал гуглить всякую всячину и кое что было для меня полезным и интересным
в частности www.natalymath.ru/index.html очень рекомендую, для тех кто далек от тервера и мат статистики или успел все забыть с университета, рекомендую.
Вернемся к теме...
Наткнулся в числе прочего вот на такой парадокс. http://ru.wikipedia.org/wiki/%CF%E0%F0%E0%E4%EE%EA%F1_%CC%EE%ED%F2%E8_%D5%EE%EB%EB%E0

Задача формулируется как описание игры, основанной на американском телешоу «Let’s Make a Deal», и названа в честь ведущего этой передачи. Наиболее распространённая формулировка этой задачи, опубликованная в 1990 годув журнале
Parade Magazine, звучит следующим образом:
Представьте, что вы стали участником игры, в которой вам нужно выбрать одну из трёх дверей. За одной из дверей находится автомобиль, за двумя другими дверями — козы. Вы выбираете одну из дверей, например, номер 1, после этого ведущий, который знает, где находится автомобиль, а где — козы, открывает одну из оставшихся дверей, например, номер 3, за которой находится коза. После этого он спрашивает вас, не желаете ли вы изменить свой выбор и выбрать дверь номер 2. Увеличатся ли вашишансы выиграть автомобиль, если вы примете предложение ведущего и измените свой выбор?После публикации немедленно выяснилось, что задача сформулирована некорректно: не все условия оговорены. Например, ведущий может придерживаться стратегии «адский Монти»: предлагать сменить выбор тогда и только тогда, когда игрок первым ходом выбрал автомобиль. Очевидно, что смена первоначального выбора будет вести в такой ситуации к гарантированному проигрышу (см ниже).
Наиболее популярной является задача с дополнительным условием № 6 из таблицы — участнику игры заранее известны следующие правила:
- автомобиль равновероятно размещён за любой из 3 дверей;
- ведущий в любом случае обязан открыть дверь с козой (но не ту, которую выбрал игрок) и предложить игроку изменить выбор;
- если у ведущего есть выбор, какую из 2 дверей открыть, он выбирает любую из них с одинаковой вероятностью.
При решении этой задачи обычно рассуждают примерно так: ведущий всегда в итоге убирает одну проигрышную дверь, и тогда вероятности появления автомобиля за двумя не открытыми становятся равны ½, вне зависимости от первоначального выбора. Но это неверно.
Вся суть в том, что своим первоначальным выбором участник делит двери: выбранная A и две другие — B и C. Вероятность того, что автомобиль находится за выбранной дверью = ⅓, того, что за другими = 2⁄3.
Для каждой из оставшихся дверей вероятность выигрыша в сложившейся ситуации вычисляется так:


Где ½ — условная вероятность нахождения автомобиля именно за данной дверью при условии, что автомобиль не за дверью, выбранной игроком.
Ведущий, открывая одну из оставшихся дверей, всегда проигрышную, сообщает тем самым игроку ровно 1 бит информации и меняет условные вероятности для B и C соответственно на «1» и «0».
После этого действия выражения принимают вид:

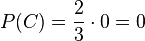
Таким образом, участнику следует изменить свой первоначальный выбор — в этом случае вероятность его выигрыша будет равна 2⁄3.
Одним из простейших объяснений является следующее: если вы меняете дверь после действий ведущего, то вы выигрываете, если изначально выбрали проигрышную дверь (тогда ведущий откроет вторую проигрышную и вам останется поменять свой выбор чтобы победить). А изначально выбрать проигрышную дверь можно 2 способами (вероятность 2⁄3), то есть если вы меняете дверь, вы выигрываете с вероятностью 2⁄3.
Этот вывод противоречит интуитивному восприятию ситуации большинством людей, поэтому описанная задача и называется парадоксом Монти Холла, то есть парадоксом в бытовом смысле.
А интуитивное восприятие таково: открывая дверь с козой, ведущий ставит перед игроком новую задачу, как бы никак не связанную с предыдущим выбором — ведь коза за открытой дверью окажется независимо от того, выбрал игрок перед этим козу или автомобиль. После того, как третья дверь открыта, игроку предстоит сделать выбор заново — и выбрать либо ту же дверь, которую он выбрал раньше, либо другую. То есть, при этом он не меняет свой предыдущий выбор, а делает новый. Математическое же решение рассматривает две последовательные задачи ведущего, как связанные друг с другом.
Однако следует брать во внимание тот фактор из условия, что ведущий откроет дверь с козой именно из двух оставшихся, а не дверь, выбранную игроком. Следовательно, оставшаяся дверь имеет больше шансов на автомобиль, так как она не была выбрана ведущим. Если рассмотреть тот случай, когда ведущий, зная, что за выбранной игроком дверью находится коза, все же откроет эту дверь, этим самым он нарочно уменьшит шансы игрока выбрать правильную дверь, так как вероятность правильного выбора будет уже ½. Но подобного рода игра будет уже по другим правилам.
Дадим ещё одно объяснение. Предположим, что вы играете по описанной выше системе, то есть из двух оставшихся дверей вы всегда выбираете дверь, отличную от вашего первоначального выбора. В каком случае вы проиграете? Проигрыш наступит тогда, и только тогда, когда с самого начала вы выбрали дверь, за которой находится автомобиль, ибо впоследствии вы неизбежно перемените свое решение в пользу двери с козой, во всех остальных случаях вы выиграете, то есть, если с самого начала ошиблись с выбором двери. Но вероятность с самого начала выбрать дверь с козой 2⁄3, вот и получается, что для победы нужна ошибка, вероятность которой в два раза больше правильного выбора.
Еще более наглядное объяснение можно дать, если представить что дверей не 3 а, скажем 1000, и после выбора игрока ведущий убирает 998 лишних, оставляя 2 двери: ту которую выбрал игрок и еще одну. Очевидно, что вероятность нахождения приза за каждой из них вовсе не ½. Гораздо большая вероятность его нахождения, а именно 0.999, будет иметь место при смене решения и выборе двери отобранной из 999. В случае с 3 дверьми логика сохраняется, но вероятность выигрыша при смене решения ниже, а именно 2⁄3.
Так вот поделившись данной статьей со своим другом и своими умозаключениями разразился спор в короый было вовлечено еще человек 6 )))
Суть спора заключается в том, что реален ли этот парадокс? Действительно ли выгодно менять мнение? Или нет ни какой разницы?
Не хочу признаваться в числе кого нахожусь, я ))) Но я в меньшинстве)))) 2 к 7 )))) Я не твердолобый, в том смысле что я действительно хочу разобраться и если я не прав, то с легкостью приму реальность....
Основная аргументация одних, это то, что «вероятность не имеет памяти» примеры с бросанием монетки (вероятность выпадения орла или решки всегда остатся 50% независимо от того что выпало ранее)
Других собственно сама статья в википедии с математическим расчетом и видео с передачи «Разрушители легенд» которое подтвержает данную теорию



















Цитата одного из нас. «Ну хорошо убрали один не правильный результат» Теперь мы знаем, что есть два варианта, вероятность того мы выбрали правильный результат равна 1/2 т.е. 50% и то изменим ли мы свой результат или нет, ни как не повлияет на изменение вероятности"
Ты понимаешь, что вероятность нахождения авто за _твоей_ дверью была и остается 1/1000, а за той другой… какая?? да, правильно 1-1/1000 = 999/1000!!! то есть почти 100%
Есть ли сомнения, что дверь надо менять? ;-))
отсюда и растет твое непонимание.
так что проставляться должны вы