SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. bstone
Мю против дельта хеджа
- 02 февраля 2019, 12:03
- |
Небольшой батл между любимчиками недавних дискуссий. Как оказалось, это может привести к расшатыванию труб и обрушению карточных домиков из опционных иллюзий. Но тем интереснее.
Итак, пусть V(S,t) — стоимость опциона для заданных параметров (страйк, вола, срок, т.п.). S — цена БА, подчиняется логнормальному процессу:

Если у нас есть позиция с купленным опционом и проданным БА, то функция стоимости нашего портфеля будет такая:
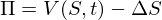
Где «дельта» равна величине нашей шортовой позиции в БА.
Как изменяется стоимость нашего портфеля с течением времени, т.е. между t и t + dt? Вот так:

C dS понятно, см. первую формулу выше. Что насчет dV? Вот тут нам как раз и нужна лемма Ито. Ее фундаментальная заслуга как раз в том, что она позволяет вычислить изменение функции от стохастической переменной S:

Никакого отношения к каким-то дрифтам вида -0.5*sigma^2 она не имеет. Это легко понять, если почитать саму лемму.
Теперь мы можем переписать формулу для изменения стоимости портфеля:

И где тут наше Мю? Да ясно где — оно в dS, см. первую формулу. Т.е. совершенно очевидно, что накапливаемые нашим портфелем прибыль или убытки напрямую зависят от Мю (оно же дрифт) в БА. Это и так интуитивно понятно. Однако, если мы отделим мух от котлет и сгруппируем изменения стоимости портфеля, которые зависят от изменений цены БА, то получим:

И тут все неявное сразу становится явным. Мол, батюшки, да если мы на каждом шаге будем шортить БА на величину, равную дельте опциона

т.е. делать наш любимый дельта хедж, то мы полностью убьем зависимость нашего портфеля от dS:

А вместе с этим мы убьем и любое Мю, которое влияет на dS.
Батл окончен и вывод очевиден. В случае с логнормальным процессом ДЕЛЬТА ХЕДЖ ПОБЕЖДАЕТ ЛЮБОЕ МЮ!
Все. Можно расходиться. Но результат лучше понять и запомнить :)
Итак, пусть V(S,t) — стоимость опциона для заданных параметров (страйк, вола, срок, т.п.). S — цена БА, подчиняется логнормальному процессу:

Если у нас есть позиция с купленным опционом и проданным БА, то функция стоимости нашего портфеля будет такая:
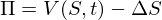
Где «дельта» равна величине нашей шортовой позиции в БА.
Как изменяется стоимость нашего портфеля с течением времени, т.е. между t и t + dt? Вот так:

C dS понятно, см. первую формулу выше. Что насчет dV? Вот тут нам как раз и нужна лемма Ито. Ее фундаментальная заслуга как раз в том, что она позволяет вычислить изменение функции от стохастической переменной S:

Никакого отношения к каким-то дрифтам вида -0.5*sigma^2 она не имеет. Это легко понять, если почитать саму лемму.
Теперь мы можем переписать формулу для изменения стоимости портфеля:

И где тут наше Мю? Да ясно где — оно в dS, см. первую формулу. Т.е. совершенно очевидно, что накапливаемые нашим портфелем прибыль или убытки напрямую зависят от Мю (оно же дрифт) в БА. Это и так интуитивно понятно. Однако, если мы отделим мух от котлет и сгруппируем изменения стоимости портфеля, которые зависят от изменений цены БА, то получим:

И тут все неявное сразу становится явным. Мол, батюшки, да если мы на каждом шаге будем шортить БА на величину, равную дельте опциона

т.е. делать наш любимый дельта хедж, то мы полностью убьем зависимость нашего портфеля от dS:

А вместе с этим мы убьем и любое Мю, которое влияет на dS.
Батл окончен и вывод очевиден. В случае с логнормальным процессом ДЕЛЬТА ХЕДЖ ПОБЕЖДАЕТ ЛЮБОЕ МЮ!
Все. Можно расходиться. Но результат лучше понять и запомнить :)
теги блога bstone
- Intraday
- LUA
- Ri
- SR
- Аллирог
- аналитик
- аналитика
- биржа
- Блэк-Шоулз
- бонус
- брокеры
- вероятность
- визуализация сделок
- Волантильность
- волатильность
- волны эллиота
- Волотильность
- герчик
- демо форекс
- депо
- депозит
- Дискреционный трейдинг
- ДУ
- интрадей
- книга
- Книги
- Коровин
- короткий стоп
- кризис
- кукл
- лчи
- лчи 2015
- Маркидон
- мобильный пост
- Нефть
- опрос
- опцион
- опционы
- опыт
- открытие брокер
- оффтоп
- просадка
- психология трейдинга
- развод
- рецензии
- рецензия
- риск
- роботы
- рублебакс
- рынок
- Сбер
- сбербанк
- Сбой на бирже
- сделки
- семинар Герчика
- си
- скальп
- слив
- смартлаб
- стакан
- стоп
- Стоп-лосс
- ТА
- технический анализ
- торговые роботы
- трейдер
- трейдинг
- улыбка волатильности
- уровни
- шорты
- Эллиот
- юмор



















Вопрос, кстати, серьезный. Ни производные считать, ни дельтахеджировать ночью не получается. Дыра у Вас в рассуждениях зияющая. Может, Вам Новиков поможет?
Не кажется ли Вам, что это напоминает сферического коня в вакууме?
1. Ваше рассуждение существенным образом зависит вида модели для процесса. Если процесс не лог-нормальный (а реальный рынок очевидно не лог-нормальный) — то эти рассуждения разваливаются и мю вполне может выжить.
2. Я не хочу делать ДХ. Зачем? Я занял статическую позицию в опционе. Очевидно, ее результат будет зависеть от мю.
Мне бы не хотелось произносить громкие слова "битва еще только начинается". Мне бы хотелось понять ключевой вопрос про формулу
CallPx = E[ PayoffAtExpiry ]
Насколько широка область применения ВОТ ЭТОЙ формулы???
1. Именно поэтому я постоянно повторял «для логнормального», «в случае с логнормальным» и т.п.
2. Будет зависеть от мю, но в реальных условиях гораздо больше от сигмы, поэтому статические позиции будут арбитражиться как халявный профит и их рыночная стоимость никак от мю зависеть не будет.
Область применения вашей любимой формулы просто ничтожна — это риск-нейтральное броуновское движение.
bstone, вот давайте на п3 остановимся.
Вы сейчас легким движением руки отметаете фундамент очень много чего.
То есть Вы утверждаете, что "оценивать равновесную цену позиции как матожидание ее выплат — это в принципе неправильно". Я Вас правильно понял?
А почему? Это тот случай когда я даже Вам не могу поверить на слово и нужны какие-то убедительные аргументы.
Когда мы рассматриваем лотереи разных видов, то стоимость участия в них всегда оцениваем через МО выплат и это не вызывает никаких проблем или сомнений. К тому же эта формула полностью свободна от предположений о виде процесса. (Кроме требования вычислимости матожидания, но это достаточно слабое ограничение, имхо.)
Я сейчас везу ребенка на занятия и выпаду из дискуссии, поэтому для затравки отвечу вам вопросом на вопрос. А почему вы считаете, что это формула правильная? Кроме лотерей, есть что-нибудь позабористей?
bstone, вы никак не аргументировали Ваши ограничения. И я с ними не согласен.
Почему правильно считать МО — для этого я делал даже отдельный топик с огромной дискуссией под ним. "Почему мы вычисляем именно матожидание?":
https://smart-lab.ru/blog/505349.php
После долгих переговоров мы все сошлись на том, что вычисление МО — это правильно и это дает именно равновесную цену при которой ни покупатели ни продавцы не имеют априорного преимущества.
bstone, https://smart-lab.ru/blog/505349.php#comment9201969
Хорошо. Уравнение Колмогорова — это круто, конечно.
Тем не менее, я Ваш комментарий интерпретирую просто как еще один способ получить формулу БШ.
Возвращаясь к формуле OptPx = E[ Payoff ]
Она применяется в рассуждениях про лотереи (а занятие статической позиции в опционе — это частный случай лотереи). Также матожидание играет ключевую роль в трейдинге в целом.
Доводы участников той дискуссии можно резюмировать так:
если опцион стоит дешевле своего истинного МО выплат — его будут покупать. Если опцион стоит дороже истинного МО выплат — его будут продавать. Как найти истинное распределение вероятности на момент экспирации — вопрос отдельный.
Таким образом именно цена OptPx = E[ Payoff ] приводит рынок в равновесное положение при котором ни у кого нет особого желания совершать какие-то направленные покупки. То есть это та самая цена, которая полностью устраивает маркет-мейкера: он выполняет свои обязательства, но при этом не получает направленную позицию. Плюс кладет в карман бид-аск спред но случайных сделках публики в противоположные стороны.
Таким образом, я рассматриваю эту формулу как фундаментальную и свободную от каких-либо ограничений.
т.е. сигма у процесса нулевая? Так это на экспу получится распределение с нулевой дисперсией. Стало быть и стоимость опциона (на любом страйке) будет нулевой. Это если МО считать через интеграл. Как получилось, что E[ CallPay ] = 50?
Т.е. в этом примере имеем нерискнейтральное распределение: его МО не равно текущей цене БА. Следовательно, считать справедливые цены опционов по нему нельзя. Формула OptPx = E[ Payoff ] пока не опровергнута :)
Вообще, приведенный процесс — не случайный. Сигма ноль, волатильность нулевая. Траектория цены — абсолютно линейная функция. Никакой случайности нет. По справедливости, в этом примере фьюч сразу должен стоить 150р. Распределение вероятностей на экспу — все 100% над ценой 150р. Дисперсия этого распределения = 0. Следовательно, временная стоимость всех опционов = 0р. И колл 150 страйка стоит 0 (и временная и внутренняя стоимость у него 0).
Т.е. контрагент дважды наварился: продал за 49 то, что стоит 0, еще и фьюч купил за 100, при справедливой цене в 150р. Ну просто жучило! :)
Кирилл Браулов, блин! =) откуда Вы 150-то берете??? Субботнее умопомрачение?
Напишите пожалуйста в явном виде функцию S(t) для цены БА как функцию времени. А то я никак понять не могу о чем Вы с bstone рассуждаете.
Но в остальном то вроде не ошибся: вола ноль, времянка ноль, стоимость любого опциона = только внутренней стоимости. Т.е. колл на 150 страйке должен стоить 271.83-150=121.83. А фьюч должен сразу взлететь со 100 до 271.83 и там оставаться весь год. Правильно?
Это если бы фьюч стоил 100. Но справедливая стоимость фьюча (для заданного процесса) должна быть сразу 272 (сами же согласились). А при такой цене фьюча колл150 никак не может стоить 0.
Получается:
1. покупатель купил за 121р колл150. На экспирации исполнил его, получил лонг фьюча по 150, продал за 272, 122 разницы — 121 уплаченной премии. Итого: +1р прибыли.
2. продавец продал за 121р колл150 и сразу купил фьюч за 272 (а не за 100). На экспирации получил исполнение, продал покупателю купленный заранее фьюч за 150, -122 разницы + 121 премии. Итого: -1р убытка
Так что, суть поменялась: теперь ch5oh в прибыли, а контрагент в убытках :)
А опцион на что: на спот или на фьюч?
Кирилл Браулов, инструмент с детерминированным поведением Вас не смущает, а дефолт по облиге смущает.
Пример крайне искуственный и к сожалению пока что он скорее уводит нас от ответа на основной вопрос.
Кирилл Браулов, он никак не аргументирует неправильность МО. А просто предлагает другой способ рассуждений (через ДХ), который по его мнению то ли дает другую цену то ли приводит к противоречиям.
Я может быть туплю «после вчерашнего», но пока что не вижу ни противоречий (только арифметические ошибки) ни серьезной атаки на метод МО.
Дело в том, что если метод блека-шолза (через ДХ) требует наличие риск-нейтральной вероятности (там это нигде не написано явно насколько помню, но допустим) и теперь bstone дает пример в явно не риск-нейтральных условиях и получает какие-то противоречия — это просто будет иллюстрацией того, что метод ДХ используют за пределами его области применения.
bstone, здрасьте. =) Я взял распределение на дату экспирации и посчитал МО. Все. Никаких требований РН нет даже близко. Также как требований безарбитражности, кстати. Нет никаких ограничений на вид СП. Красота.
bstone, а чего он «неправильный»? Колл стоит ровно столько, сколько он принесет в момент экспирации.
Может, у Вас ДХ разваливается потому что в предложенной модели нарушается требование безарбитражности? Что бы оно не означало на самом деле.
bstone, какую цепочку действий Вы предлагаете, чтобы получить "арбитраж с использованием ДХ"? Напишите, пожалуйста, еще раз компактно. А то мы начали вообще с неправильных чисел, потом на 100 комментах размазали уточнения. Ну и формулу для дельты заодно.
Имхо, если мы договорились, что
(1) S(t) = 100*exp(t)
и, следовательно,
(2) CallPx(t) = MAX(0, So*exp(1)-K)
тогда
(3) дельта кола становится ступенчатой функцией и равна 0 для всех колов страйка меньше So*exp(1).
Вроде бы, все расписал подробней некуда. Ищем точку несогласия.
По хорошему, тут надо проводить следственный эксперимент. Завести два независимых портфеля: в первом реально купить опцион, во втором виртуально его продать и включить реальный ДХ. И потом сравнить их эквити. Насколько понимаю: БШ, Кирилл Ильинский (его фраза: «стоимость опциона — стоимость его хеджа»), bstone, Дмитрий Новиков (и вообще все кто считает, что опцион можно симулировать голым фьючом) утверждают, что эти эквити будут полностью одинаковыми. А мне кажется, если захватить достаточно большой период времени (чтобы там и гэпы были, и наоборот периоды застоя с временным распадом), то эквити будут достаточно сильно отличаться. Корреляция будет, но не 100%. И финальный PnL может довольно сильно будет отличаться. А если бы не отличался, вот тогда бы можно было утверждать, что метод «через ДХ» имеет право быть. Вот бы кто такой эксперимент замутил…
Кирилл Браулов, с какого перепуга он должен «сразу» скакнуть на 272???
Динамика цены определена моделью процесса.
Это вообще не акция, а что-то типа преддефолтной бескупонной облигации: мы ее покупаем за копейки (за 100) и далее она растет по экспоненте к дате погашения. Или специальный ETF (типа FXMM) с детерминированным законом поведения.
bstone, туше.
C(K) = MAX(0, 272-K)
В общем, мы обсуждаем странную предельную модель, которую можно считать, но в которой все числа выглядят очень странно.
К сожалению, это только отодвигает нас от ответа на основной вопрос.
bstone, разумные цены будет давать.
Собственно, еще раз повторюсь: если Ваши рассуждения через ДХ начинают разваливаться в этих условиях (что пока что тоже не продемонстрировано), это говорит только о том, что Вы применяете их за пределами их области действия.
bstone, Вы еще даже дельту не посчитали, а уже делаете выводы.
Удобно занимать направленную выигрышную позицию в БА, если про него все известно. Купите 10 фьючерсов, чего мелочиться? И скажите потом, что это выгоднее, чем покупать колл за 122.
Еще раз пример. Пусть на рынке только двое участников: A (который считает что справедливая цена колл150=122) и B (считает, что колл150=0). А выставляет бид колл150 на 121р. B радостно ему продает.
На экспирации А исполняет свой опцион, получает лонг фьюча по 150, продает его за 272, 122 разницы — 121 уплаченной премии. Итого: +1р прибыли. B очевидно получает убыток -1р (других участников в рынке нет, а комис не учитываем). Значит 122 была справедливой ценой, а 0 — нет.
Или в примере я где-то ошибся?
Во вторых, тут надо привлекать третьего участника: C. Который делает сказочный подарок B и продает ему фьюч за 100р, хотя оба знают, что на экспу БА будет 100% стоить 272р. Т.е. в таком примере, участник B остается в прибыли только за счет лоха С, а не за счет «неправильно» посчитавшего справедливую стоимость опциона участника A. Если бы C продал по правильной цене фьюч (по 272), то у B опять же был бы убыток -1р, как и в моем примере.
Все-таки скажите, в моем то примере (когда только два участника) — есть ошибка или нет? Из него ведь четко следует, что 122 правильная цена опциона, а 0 — нет.
Насчет лоха С — это жизненно. Стас Бржозовский любит об этом сигналить, когда и продавец, и покупатель опциона заработали, а С потерял.
Если ваш пример о том, что базовый актив вообще не торгуется, то он правильный, но опционов без БА не бывает.
Если согласны, что в моем примере ошибок нет, то соглашайтесь уж и что справедливая цена колл150=122! А то топик кипит уже от перегрева и наши с ch5oh комменты скоро в ленту не будут влезать :)
Окей, новая вводная:
dS = mu*S*dt + sigma*S*dX
mu = 0.5
sigma = 0.2
K = 150
S0 = 100
T = 1
Арбитражность зарыта в этих условиях?
Монте-карлим процесс с шагом 1/365 и считаем две вещи: реализованный Payoff и PnL продавца, который делал ДХ по 20% воле. Тысяча симулляций.
Распределение БА (здесь и далее частоты):
Распределение Payoff:
E[ S ] = 171.10 руб.
E[ Payoff ] = 22.04 руб.
Покупатель ставил бид на 21 руб. Распределение PnL продавца, продававшего опцион по 21 руб.:
E[ PnL ] = 20.93 руб.
Итого, покупатель кола зарабатывал в среднем 1.04 руб, продавец — 20.93 руб.
Живите теперь с этим :)
bstone, так ведь разобрались еще на Вашем примере предельном (кстати, в итоге он оказался вполне полезен):
продавец кола когда делал дельта-хедж на самом деле просто занял направленную позицию во фьючерсе и насладился положительным мю.
А покупатель кола — он был лишен этого удовольствия. Зато положил в карман гарантированный 1 рубль. Что в условиях неопреденности на величину мю на реальном рынке само по себе приятно.
smart-lab.ru/blog/519978.php#comment9392911
bstone, Вы бы нас еще паритетом попугали: можно заметить, что в оригинальном примере пут страйка 150 стоит 0. То есть c-p=122
Живите теперь с этим :)
Кирилл Браулов, обратите внимание: +171 рубль — это ровно прибыль покупателя фьючерса (с поправкой на 1 рубль за глупость). То есть вся прибыль "продавца опционов, который делает ДХ" — это прибыль фьючерса, который вырос со 100 до 272.
И это логично. Потому что колл страйка 150 никак не меняется в цене в процессе этого упражнения. А не меняется просто потому, что финальная цена куда прилетит фьюч одна и та же на протяжении всей траектории.
Таким образом, мы получаем следующую историю:
А. 150-й колл стоит 122 рубля — потому что ровно на 122 рубля БА будет выше страйка на экспирацию. Это «истинная цена кола». Речь не идет о том, что покупатель опциона что-то заработает. Потому что этот колл вообще не меняется в цене.
Б. Фьючерс на самом деле стоит 272 (недооценен на 172 рубля). Покупатель фьючерса по 100 — молодец и герой.
В. Продавец фьючерса — "большой терпила номер 1" и оплачивает банкет покупателя фьючерса.
Д. Как бы очень умный продавец опциона продает его по 121 и на самом деле сразу дарит 1 рубль покупателю опциона. Далее, этот гений ДХ «хеджируется БА» (в количестве 1 штука по 100) и наивно радуется итоговой прибыли в размере 171 рубль. То есть фактически он является "маленьким терпилой номер 2" и оплачивает семечки покупателю колов (который купил их по 121 вместо истинной цены 122).
Кажется, благодаря коллеге Кирилл Браулов, который предложил подробно расписать роли и финрезы участников рынка, мы поставили все на свое место.
При этом метод МО позволяет разобраться в ситуации и вычислить все цены без необходимости привлечения зубодробительных дифуров в частных производных.
Да здравствует МО! Да здравствует Оккам!
ПС Заодно можно заметить, что пут страйка 150 стоит 0.
Паритет пусть каждый сам посчитает, ужаснется и живет с этим.
Кирилл Браулов, БА будет «взлетать» постепенно в соответствии со своей динамикой
S(t) = 100*exp(t)
ПС В данном случае t — это не время до экспирации, а прямое календарное время, отсчитанное от текущего момента.
bstone, без аргументов у нас разговор как у детей в детском саду: "у меня мама лучше — нет у меня папа лучше". Извините, но не ожидал от Вас скатывания на дошкольный уровень.
Цена данного 150-го опциона очевидно 122. И это полностью разумно и соответствует тем деньгам, которые с него можно будет получить в момент экспирации.
bstone, так. Стоп-машина. Полагаю, надо просто остановить диалог.
Теперь будет мой черед написать пост и показать красоту и силу подхода через МО.
До связи! Хорошего воскресенья. =)
Кирилл Браулов, Вы неправильно цену данного кола посчитали. Распределение — конечно не риск-нейтральное. Ну и что? Ну, сложились такие условия в силу каких-то причин. На рынке стоит кем-то забытый офер 100 при том, что всем очевидно, что БА уже должен стоить 110-150.
Таких оферов на каждом гепе по 100 штук сносят.
bstone, процесс детерминированный. Что там еще монтекарлить?
S(t) = 100*exp(t)
Кирилл Браулов, она очевидно ненулевая. Процесс детерминированный, поэтому мы точно знаем куда добежит БА за время до экспирации.
Если я правильно понимаю,
S(1) = 100*exp(1) = 271.83
Значит, цены колов как функция страйков выглядит очень просто:
C(K) = MAX(0, K-271.83)
Следовательно, указанный уважаемым bstone колл страйка 150 действительно стоит 0.
С моей стороны будет очень глупо покупать его по 50 и я не понимаю почему уважаемый bstone, который легко вертит дифуры в частных производных написал, что "E[ CallPay ] = 50"
Уверен, это недоразумение, вызванное желанием ответить мне как можно скорее даже в полевых условиях.
bstone, Вы неправильно написали, что матожидание этого кола равно 50.
Я полностью с Вами согласен, что стоимость данного кола равна 0, поэтому ставить биды ни по 50 ни даже по 1 я, конечно, не буду.
Формула стоимости колов в общем виде для предложенного процесса:
C(K) = MAX(0, K-271.83)
А как, например, страховые вычисляют КАСКО с франшизой? Они же это сразу считают. Я как-то мучал своего агента: а сколько будет с франшизой 30тр? Он сразу: 50тр. А с франшизой 50тр? 40тр. А со 100тр? 20тр. (цифры условны, точных не помню). Как он это делал? Быстро на коленке прикидывал? Смотрел — какие цены у конкурентов? Не успел бы. Единственный вариант, имхо, это используя статистику страховых случаев (распределение вероятностей) посчитать матожидание выплат, добавить маржу — вот и готовая цена страховки. Мне кажется, других вариантов нет.
Как насчет: «гэп vs ДХ»? Думается, что тут уже ДХ проиграет.
И поскольку гэп в каком то смысле заложен в мю реального процесса (не сферического в вакууме логнормального, а приближенного к реальности, учитывающего гэпы), то получается, что ДХ проиграет реальному мю. И эпик-фейл Коровина — тому подтверждение.
Что же касается сказки о логнормальности и ее адептов, не учитывающих не только возможность временного прекращения торгов на несколько дней из-за большой скорости падения, но даже появления периодов с сериями огромных гэпов, то наверно следует рассуждать о свойствах психики, жаждущей веровать.
Как это не было? А что же это такое было 9 апреля с 4мя планками подряд?
По моему, это очевидный гэп.
Мне кажется, что ТФ не важен для выявления гэпа. Правда, под гэпом пониманию не разрыв цены (в одном тике одна цена, а в следующем цена сделки уже отличается сразу на много шагов цены), а мощное движение цены, не вписывающееся в обычное случайное блуждание. То, которое и дает толстые хвосты распределению вероятностей (где окажется цена БА на экспу). Мне кажется, 9 апреля было именно такое движение.
Кирилл Браулов, у Вас свое и нестандарное понимание термина «геп».
Общепринятое понимание слова «геп» состоит в том, что «разница между последним трейдом вчера и первым трейдом сегодня очень большая».
Иногда можно немного расширить это определение и обсуждать не первый трейд за сегодня, а «первую цену за сегодня по которой реально зайти обычному ритейл-клиенту».
Тогда гепы надо искать так: на таймфрейме М1 выбрасываете первую свечу каждого дня и смотрите разницу цен между клоузом вчера и ценой в 10:01. Если разница «офигенно большая» — это геп.
Поэтому Вы и не понимаете друг друга со "старым новичком" ( старый трейдер ), что вкладываете разный смысл в одно и тоже слово.
9 апреля реальный рынок давал возможность торговать не менее 50-и минут до первой планки, ГО не повышалось, стаканы не пустели, новость медленно расходилась по рынку. Если коровоанохины не предпринимали никаких попыток управления, то можно усматривать в этом признаки умысла.
Мне кажется, было примерно так: «Главное не бздеть, продаем на всю котлету, я суперпрофи, 20 лет опыта + 1001 способ управления проданным краем… Так, брокер, дай в долг! Не крой позу!!! Видишь дельта то в ноль, а на вегу наплевать, подожди и все успокоится… Ааа, биржа — ты чо по беспределу ГО так повысила!!!.. Ааааааааа, брокер — не смей крыть нас по стакану!!!!!!....... Так, пасаны, биржа и брокер оказались бяками, тиснули ваши денежки — я ни при чем. Кто остался — переходим на Америку и теперь играем от покупки...»
Кирилл Браулов, коранохины не делали ДХ, поэтому и вылетели в трубу.
Сейчас не нужно притягивать сложности из реального мира: ночные гепы, выходные, комиссии, ликвидность и пропадание интеренета потому что таджики перерубили кабель.
Надо разобраться в краеугольном камне всего опционного мира: нужно ли считать матожидание выплат или надо применять какой-то другой трюк? Коллега bstone предлагает все делать через ДХ. Но это не единственный способ. И нам желательно выяснить какой из способов «более фундаментальный» или «имеет бОльшую область применимости»?
Нельзя ведь с помощью голого фьюча повторить нелинейный взлет опциона после гэпа. Повторить опцион голым фьючом при небольшом случайном блуждании БА — можно. А гэп — ну никак :)
Кирилл Браулов, их могло бы (теоретически) спасти, если бы они были крутые скальперы и взяли шорт фьюч "на всё и даже больше".
Но бог с ними с трупами.
Вы мне свое мнение про МО скажите. Вроде бы, в предыдущем обсуждении у Вас не было сомнений, что надо считать МО и танцевать именно от МО.
Ну и про гепы. Они нормально отрабатываются. Был у меня как то опцион BAC, купленный. С хеджеми акциями. Перед открытием сессии, я вижу, что на предмартете цена улетела. Отлично, БА не полз, а сразу подорожал. Открывается маркет, и что? Вола просто рухнула на величину гепа. Ну не заработал еще ММ, что бы мне премию платить. Опцион это стоимость ДХ.
Насчет «гэп заложен в мю» — не утверждаю этого 100%, просто возможный взгляд. В самой первой формуле этого поста можно же мю и сигму рассматривать не константами (как это делают БШ), а новыми случайными процессами. И когда моделируем гэп, то соответствующее приращение цены генерируем через мю. Ну и сигма заодно сразу после гэпа взлетает (чтобы потом плавно снижаться к своему среднему). Во всяком случае, я именно так запрограммировал у себя случайный процесс, который генерил распределение (улыбку) похожее на рыночное. Возможно, был неправ и надо было гэп учитывать отдельными третьим/четвертым слагаемым, а не впихивать его в мю и сигму.
применительно к страховым случаям (ну или к стандартной «банковской книге») есть ориентиры Ожидаемых потерь — от них поправка в ст-ти (страховых) продуктов (и для их оценки не нужна нормальность/логнор).
для всего остального, т.е. unexpected (а именно таким было 9.4.18, 3.3.14 и пр.) есть капитал (у субъектов кредитного/страхового рынков), в случае К. — ГО
З.ы: Тут как раз надо вспомнить 'нормальность' и сигмы. Ну и понятно, что речь не идет о более-менее систематических гэпах (аналитически отражабельных на μ)
убыток 0.1*A — вероятность 20%
убыток 0.2*A — вероятность 5%
...
убыток 0.9*А — вероятность 0.1%
убыток 1*А (тотал) — вероятность 0.01%
(A — стоимость авто)
то, мне кажется, по нему вполне можно рассчитать страховую премию с любой франшизой.
(как минимум по фактору сайза) идентичное дискр. распределение
академические) подходы в том чтобы сделать сферического коня: лимитировать кол-во контрактов с разными кат клиентов (для которых риски выше — ниже лимит, и обратно). это достаточно нетривиально сделать с достаточно однородными категориями Активы.
для каждой из (относит небольшого числа) категорий Y, будешь иметь распределение, характеризующее (н-р, скорее частоту события) со своими параметрами. а лось по каждой категории произведение =f(Y)*Pa
Pa — ст-ть имущества, как-то так, если грубо )).
сорри, оч. унылый интернет-линк у меня — нормально ниче не поститься( коммент восстановлен из кода страницы
KLoYH, =) опционщику должно быть стыдно в этом признаваться.
Да и нет здесь дифуров никаких. Школьная алгебра средних классов.
KLoYH, ограничение на сумму участия меня больше не устраивает. Один раз попробовали — хватит. Давайте указывать дневной финрез в процентах? Сергей всех умножит на 100 000 стартовых — и будет квази-эквити.
Кстати, тогда, наверное, и Стас Бржозовский согласится участвовать как отдельный участник, а не в виде 2-в-1.
bozon, сходу не понял, но звучит прикольно.
А с какого перепуга волатильность имеет фиксированный дрейф??? Понятно, что у Вас все взрывается. Вы либо своливаетесь в состояние с нулевой волой (или даже отрицательной) или уходите в зону бесконечной волатильности.
Не, мне эта модель не нравится от слова совсем.
bozon, когда пишут Величина = А*dt + B*dZ , то коэффициент A обычно означает фиксированную константу. Иначе мы получаем модель неограниченной свободы с неограниченным числом подгоночных параметров.
Чтобы Вас правильно поняли, напишите отдельный пост. Расскажите про эту мега-модель, распишите вид функции A. Тогда, может быть, мы с Вами будем говорить на одном языке.
Пока что Вы мне напоминаете А. Г. , который называет рынок нормальным процессом на основании того, что вроде как может записать его в виде N(m(t,F), s(t,F)) где сами функции m, s являются смесью детерминированных функций и случайных процессов различных априорно не указанных видов.
С чем я не согласен, потому что предпочитаю называть кошку кошкой.
Но вот мы продаем дальний пут и покупаем дальний колл, гамма в 0. Откуда тогда бабло. Дельту мы тоже в ноль. Пока гамма в 0 ДХ генерить ни чего не может. Так? Ну за шорт, если это акции, но это в цене опциона. И кто мне скажет, что это не МО?
bstone, что значит "возьмите mu=0.3 и подставьте в формулу Блека-Шолза"? В формуле БШ нет параметра мю.
bstone, можно я сыграю в тупого?
Мне как бы пофиг что там лежало в исходных аксиомах и какие буквы использовались. Есть итоговая формула. В ней нет мю. При всем желании я не могу подставить в формулу БШ параметр мю=0.3, если в ней его нет.
bstone, прочитал. Вот обратил внимание на последнюю фразу:
> "В случае с логнормальным процессом ДЕЛЬТА ХЕДЖ ПОБЕЖДАЕТ ЛЮБОЕ МЮ! "
А если процесс будет не ЛН???
Что тогда?
Известны ли Вам примеры процессов для которых этот вывод неверен?
Дмитрий Новиков, нет. БШ сначала декларативно уничтожил МО, а потом стал писать формулы. Ну, не умел он толком брать интегралы, что поделать.
Или (что более вероятно) — от него это и не требовалось. Все-таки целая отрасль финансов возникла только потому, что много хеджеров начали думать, что они понимают в опционах. А по факту просто сливали деньги селл-сайду. То есть крупным инвест.домам.
Я бы на месте голдмана тоже БШ нобелевскую копеечку кинул за такой подгон удачный.
Дмитрий Новиков, (устало) давайте не будем притягивать сюда реальный мир, улыбку и слив депо по пьяни?
Мы (коллеги) никак не можем договориться насчет правомерности вычислений через МО, а Вы уже со своей улыбкой лезете.
Если Вы согласны с формулой CallPx=E[ Payoff ] — тогда можно легко показать как возникает улыбка. Если не согласны… Ну, не знаю. Я что-то подустал от разговора. Будете так и жить несогласные. =) И верить, что рынок — гаусс.