Основы статистического арбитража. Коинтеграция.

Собственно, понятие коинтеграции и лежало, в основе статистического арбитража, который только начал появлятся в конце 80-х и позволил первопроходцам из JP Morgan, нарубить не мало денег, пока…, но об этом в конце статьи. Поэтому в этот раз мы поговорим, про коинтеграцию, что это такое, зачем и почему. Но начнем из далека и рассмотрим такие статистически понятия как порядок интеграции процесса, и фиктивной (spurios) регрессии, которые и лежат в основе. 

Рассмотрим для начала простейший процесс, гауссовский шум:


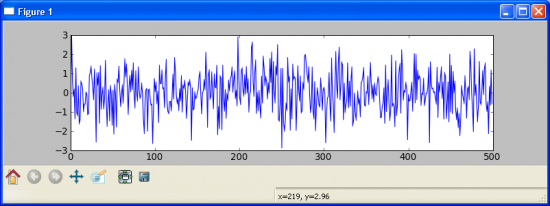
 Теперь построим его кумулятивную сумму, то есть возьмем значения и последовательно их сложим, таким образом получим что Y_i = sum k = 0..i X_k, где X_k — это исходный гаусовский шум, Y_i — результирующий процесс. То есть в данном случаи взяли шум и его проинтегрировали, таким образом получив случайное блуждание. Так же мы можем повторить данный процесс еще раз, но на этот раз взяв в качестве исходных значений, полученное нами на предыдущем шаги случайное блуждание. Таким образом получим (сверху — интеграл шума, случайное блуждание, снизу — повторная сумма но на этот раз взятая по случайному блужданию):


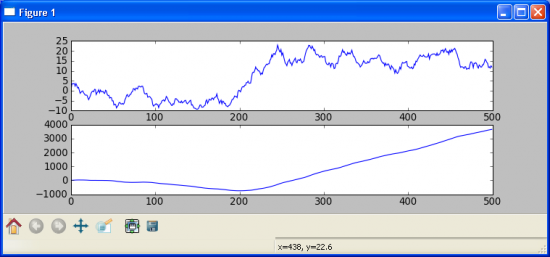
 Проще говоря мы проделали следующее, мы взяли числовой ряд шума, и применили к нему операцию кумулятивной суммы (интегрирования), после первого применения мы очевидно получили случайное блуждание, после последующего применения получили еще один числовой ряд. Чтобы опять вернуться к шуму нам так же дважды необходимо применить операцию конечной разности к этому числовому ряду(или один раз к случайному блужданию). Тогда количество раз применения операции кумулятивной суммы — мы можем назвать порядком интеграции процесса(числового ряда). То есть порядок интеграции процесса, это то сколько раз мы применили сумму к шуму, или наоборот сколько раз необходим применить конечную разность к процессу чтобы получить шум(гауссово распределенную случайную переменную). В общем случаи, шум заменяется на требование получения стационарного процесса(то есть числового ряда у которого мат ожидание и АКФ не изменяются во времени). Процесс с порядком интеграции k, мы будем обозначать как I(k).

К примеру, график цены можно отнести к I(1) процессу (случайному блуждания), если мы возьмем, приращения, то есть к разницу Close-Open свечек, то получим процесс с порядком интеграции I(0). Если рассмотрим какие-то экономические индикаторы к примеру ВВП или объем различных агрегатов денежной массы, то получим процессы близкие к I(2).

Широко известны случаи, когда между абсолютно не связанными числовыми рядами находилась корреляция, к примеру, между уровнем цен и уровнем осадков в Великобритании, или поголовьем овец и GDP. Все это примеры фиктивной регрессии (spurious regression). Рассмотрим для примера, два независимых случайных блуждания:



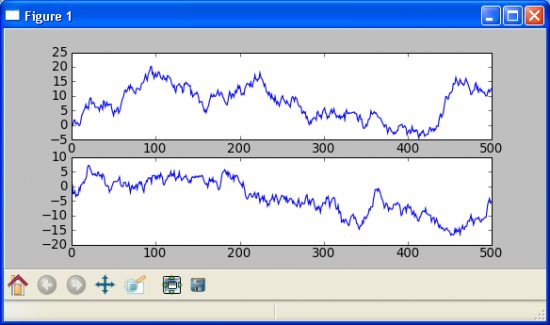
 Коэффициент корреляции между ними = 0.35, хотя они и не взаимосвязаны. Вспомним, что корреляция связана с линейной регрессии, и рассмотрим взаимный график первого и второго процесса. (по оси x — отложен первый процесс, по оси y — второй):
 

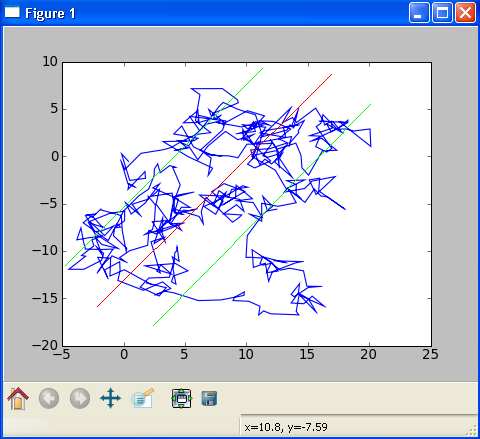
 Фактически расчет обычной корреляции сводится к следующем, мы считаем какой процент времени, два процесса находятся совместно по одну (или разную, если корреляция отрицательная) сторону от нуля. Но как известно, для случайного блуждания вероятность нахождения по одну сторону от нуля подчиняется закону арксинуса, соответственно, когда мы пытаемся посчитать корреляцию между двумя случайными блужданиями вероятность, что они чисто случайно ушли от нуля в одну сторону, значительно больше нуля, таким образом коэффициент корреляции начинает нам показывать не валидную взаимосвязь между двумя процессами, которой на самом деле нет.

Каким же образом, нам посчитать взаимосвязь между двумя процессами? Для начала дадим простой ответ на этот вопрос. В общем случаи коэффициент корреляции валиден, если два числовых ряда для которых он расчитывается являются независимо распределенными случайными переменными (белым шумом, который мы рассматривали в начале статьи), или по крайней мере стационарными процессами. Таким образом, оба числовых ряда должны быть оба нулевого порядка интеграции (I(0) — белый шум/стационарный процесс). То есть чтобы к примеру, посчитать взаимосвязь между двумя акциями(I(1) процессами), необходимо взять разность (Close — Open) и считать корреляцию между ними. Если мы рассматриваем денежную массу/GDP, или другие процессы близкие к I(2), конечную разность необходимо брать два раза, чтобы привести их общему знаменателю I(0) процесса.

Минусы данного подхода заключаются, в том что для коротких числовых рядов, расчет корреляции после взятия конечных разностей может не давать достаточной статистической значимости, а так же в том что сама выявляемая взаимосвязь между двумя процесса достаточно примитивна.

Более сложный ответ на вопрос, «как посчитать взаимосвязь между двумя процессами», привел Клайва Грэнджера и сотоварищи, к Нобелевской премии, революционизировал статистический анализ/эконометрику, и название ему — коинтеграция. 

Рассмотрим все те же два случайных блуждания Y1, Y2 (I(1) процесса). Теперь подумаем над тем, как будет вести себя разность между ними S = Y1 — b*Y2(где b какой-то коэффициент, для простоты возьмем = 1). Если процессы не взаимосвязаны, то эта разность S так же должна быть случайным блужданием, то есть I(1) процессом. Если же взаимосвязь есть, то S должна быть «чем то меньшим» в статистическом смысле чем случайное блуждание. К примеру если мы представим два числовых ряда которые недалеко отходят друг от друга, то разница между ними будет белым шумом. В этом и заключается смысл коинтеграции, если для какого то коэффициента b спред S = Y1 — b*Y2, будет иметь меньший порядок интеграции, чем исходные процессы, тогда процессы коинтегрированны. В расмотренном выше случаи, это будет обозначать что для двух I(1) процессов, порядок интеграции спреда S должен быть I(0) (то есть белым шумом/стационарным), для какого-то значения коэффициента b. 

Рассмотрим, так же для примера, разность двух случайных блужданий, для которых мы ранее насчитали корреляцию 0.35. Получим, такое же случайное блуждание:



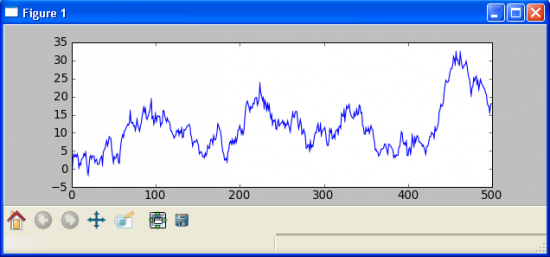
 Теперь рассмотрим два случайных блуждания, но на этот раз взаимосвязанные, и разницу между ними, которая в данном случаи очевидно является стационарным I(0) процессом. (сверху — первое случайное блуждание, посередине — второе, снизу — разница/спред между ними).



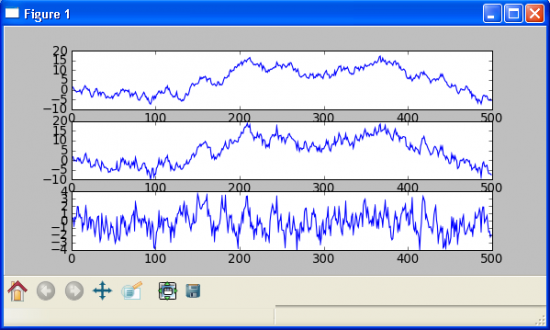
То есть логика коинтеграции, сводится к тому что, необходим найти какой-то коэффициент b, и построить спред S = Y1 — b*Y2, такой что порядок интеграции спреда меньше чем у исходных процессов. Если мы рассматриваем два I(1) процесса, то спред должен быть стационарен.

Так же в качестве примера коинтеграции, часто приводят такой жизненный пример, представим пьяницу (случайное блуждание) и собаку которую он ведет по улицы на поводке. Теперь если мы представим их позицию как два числовых рядов. То получим следующее, что один процесс движется случайно (пьяница), а другой (собака) хотя и может убегать от него в ту или иную сторону, но не может убегать от него далеко и всегда возвращается. Соответственно если мы построим разницу между ними она будет иметь меньший порядок интеграции, чем два совершенно несвязанных случайных блуждания (пьяницы, блуждающие независимо по городу).

Хорошо, мы предположим знаем что два процесса коинтегрированны, но что нам это дает, какую математическую модель можно использовать чтобы отразить их динамику? Существует теорема о репрезентации коинтеграции, которая говорит нам следующее, что для двух коинтегрированных числовых рядов, существует ECM(error correction model) модель, а так же что если для двух рядов существует ECM модель то они коинтегрированны. Проще говоря коинтеграция <-> ECM модель, то есть существование коинтеграции влечет наличие ECM модели, и наоборот. В простейшем случаи, она описывает следующие соотношения, предположим что мы построили спред S между двумя рядами. Тогда каждый процесс будет стараться вернуть спред к нулю, то есть приращения процессов должны быть скоррелированны с положением спреда. Таким образом мы приходим к следующей модели, для двух рядов Y1 и Y2, мы строим спред S = Y1 — b*Y2, и разности каждого из них dY1, dY2. Чтобы спрэд не «уходил далеко», разности процессов должны быть с ним скоррелированны. То есть постоянно подстраиваться, как в примере пьянице и собакой, там действует по сути один процесс пьяница, а собака к нему привязанна, в общем случаи мы расмматриваем — двух пьяниц но связанных резинкой, когда спред расходится, то соответственно начинают действовать силы возвращающие его к равновесию. Таким образом мы приходим к следующей модели корректирвки ошибок (ECM модели):
dY1 = -a1*S + lagged(dY1, dY2)
dY2 = -a2*S + lagged(dY1, dY2)
то есть, наличие коинтеграции одназначно обозначает, скоррелированность приращений процессов и спреда. Если спред расходится, то есть к примеру становится положительным, то приращения одного процесса обратно скоррелированного с ним возвращают его к нулю, так же как и приращения другого. В этом смысл ECM модели, а так же коинтеграции, так как наличие ECM модели эквивалентно коинтеграции и наоборот. Коинтеграция — показывает что какая-то зависимость между числовыми рядами есть, ECM модель — дает конкретное выражение этой зависимости в виде их динамики. 

В общем случаи, коинтеграционной зависимостью могут связаны больше чем две переменные, а так же таких зависемостей между ними может быть несколько, что приводит нас к VECM модели (vector error correction model) — тягловой лошадки современной эконометрики.

Единственный вопрос, который мы пока не затронули, это то каким образом, строить спрэд (то есть числовой ряд S). Если нам дан набор числовых рядов Y1..Yn между которыми присутствует единственная коинтеграционая зависимость, то для оценки параметров b1-bn спреда вида S = Y1 — b1*Y1 — b2*Y2… — bn*Yn, достаточно построить линейную регрессию между Y1 ~ Y2..Yn, коэффициенты которой(как доказывается в мат. статистике) дадут консистентную оценку параметров b1..bn. В простейшем случаи когда процесса всего лишь два, необходимо той же простейшей линейно регрессией Y1 ~ b*Y2, определить значение коэффициента.

Почему коинтеграция так важна? Потому что подавляющее большинство макро экономических переменных/индикаторов нестационарны, и поэтому трудно поддаются анализу классическими статистическими методами, но в тоже время имеют очевидную схожесть между собой (не разбигаются далеко, как в примере с пьяницей и собакой) и поэтому могут быть валидно описанны при помощи коинтеграции и соответствующих моделей (VECM etc). 

Но применительно к рынку, наличие настоящей коинтеграции означает — наличие абитража, что противоречит базовому постулату эффективных рынков — no arbitrage. Настоящий спред для коинтегрированных процессов, всегда (!) сходитя, так как является стационарным I(0) процессом. Так же для двух коинтегрированных процессов, всегда должна существовать ECM модель(то есть приращения активов должны быть обратно скоррелированны со спредом, возвращая его к нулю). Для рыночных спредов не наблюдается ни того ни другого, поэтому хотя они и ограничены, и могут проходить тесты на коинтеграцию, у них есть главное отличие — рыночные спреды не стационарны.

Клуб алготрейдеров StockSharp
Роботы на заказ

Ссылки на статьи про коинтеграции:
http://lipas.uwasa.fi/~sjp/Teaching/Afts/Lectures/etsc33.pdf
http://advances.mse.ac.in/lecture/notes3.pdf
http://www.uh.edu/~bsorense/coint.pdf