Блог им. Gusan
Модель Курбаковского, сглаживание и нормировка
- 14 декабря 2019, 13:03
- |
Большое спасибо Виталию Курбаковскому, что опубликовал свою обобщенную модель ценообразования опционов (1, 2, 3, 4, 5). Давно хотелось подобную модель, с минимум параметров, физический смысл которых был бы более-менее понятен. Чтобы можно было осознано свои параметры модели задавать, а не подгоняться под рынок и слепо за ним идти. Модель, которую использует биржа (с шестью параметрами ABCDES) под такой запрос не подходит. Попробуй там пойми, все ли шесть параметров сейчас имеют справедливые и оправданные значения, или с каким-то из параметров можно поспорить. И слишком уж она гибкая. Бывало смотришь — выскочила какая-то котировка за модель, только соберешься по ней ударить, а программа параметры модели подкорректировала и услужливо изогнула кривую с учетом новой котировки. И то, что только что
выбивалось за модель, стало ей соответствовать. Пробовал еще модель китайской улыбки, там и параметров поменьше и смысл у них попонятнее, но очень уж плохо она подгоняется под рынок. И тут, на счастье, Виталий поделился своей моделью и все подробно объяснил. Реализовал у себя и оказалось — то что надо. И в рынок хорошо вписывается, и параметры имеет понятные.
Добавил в модель немного отсебятины. Хочу поделится, может кому тоже пригодится, а может кто покритикует/посоветует чего. Проблема в том, что если считать дельту просто по формуле, то получается скачок при переходе через ЦС. И если пересчитать цены в улыбку IV, то получается линейная галочка. С одной стороны — улыбка IV вроде как бессмысленная сущность и являет собой просто набор поправочных коэф-тов. Но с другой стороны все таки нет-нет, да и посмотришь на улыбку. И как-то не по себе, когда вместо привычной плавной параболы видишь угловатую галочку. Виталий написал, как сглаживать дельты, но как сглаживать сами цены пока не ответил. Стал кумекать — как бы попроще все сгладить без лишних вычислений и придумалось такое:
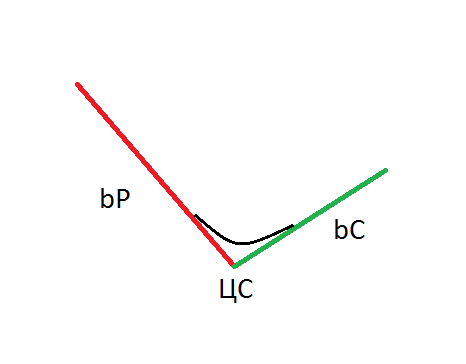
Решил просто сгладить переход между bP и bC с помощью ф-ции Tanh (гиперболический тангенс). Причем коэф-т сглаживания (широко или узко сглаживать) стал нормировать на время и на относительное расстояние страйка до ЦС. Заменил везде, где у Курбаковского:
b = bc
If S < x Then b = bp
на такое (это уже Паскаль):
b := bP + (bC — bP) * (1+Tanh(Ln(S/x)/Sqrt(T)/CoefSmooth))/2
И получилось замечательно. Улыбки стали на загляденье, с плавными донышками. Ушел скачок в дельтах. И главное: один и тот же коэф-т сглаживания (CoefSmooth) одинаково хорошо подходит для разных календарных серий. И даже у разных БА довольно близок. Например, для Ri подошел 0.05, а для Si 0.04.
Обрадовавшись этому результату, решил попробовать еще нормировать параметры bP и bC. Чтобы они тоже не зависели от времени до экспирации. Вот история этих параметров (для RTS-12.19M191219):
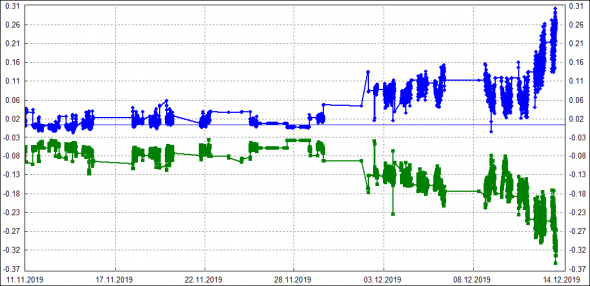
Попробовал сначала в лоб и везде в формулах заменил (S-x), на Ln(S/x)/Sqrt(T). Т.е. как-бы заменил абсолютное центрирование на относительное, да еще и на время нормировал. Но не тут то было, программа не смогла подобрать параметры модели, чтобы теорцены подходили под рынок. Возможно, при такой нормировке и mI нужно считать как-то по другому. Как — не придумал. Решил просто подобрать ф-ции под историю bB/bC. Видно, что они изменяются симметрично. Ось симметрии, кстати, на уровне -0.03. А по моим прикидкам, на Ri параметр bK можно как раз оценить около -0.03:
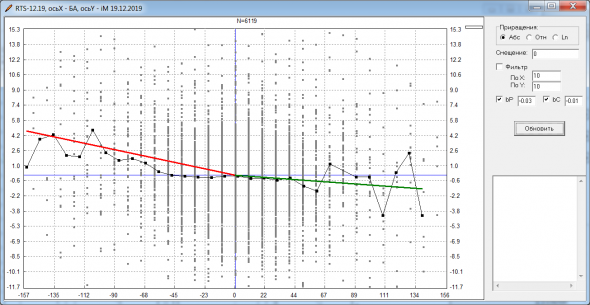
Решил, что это не спроста и неслучайное совпадение. Виталий же писал, что в теории должно было быть: bP=bC=bK. А тут получается, что оба коэф-та и bP и bC берут свое начало с bK, и потом со временем симметрично разъезжаются. Приготовился к долгим поискам, но уже с третьей попытки подобрал простые формулы:
bP = bK — 1/T
bC = bK + 1/T
Вот как они накладываются на историю:
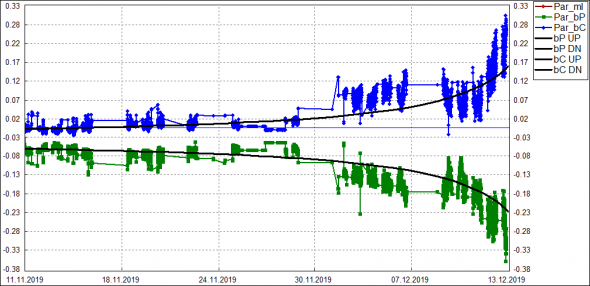
Наверное, не очень хорошо вот так, не понимая сути, просто методом тыка подбирать коэф-ты и зависимости. Но зато теперь вместо модели с тремя динамическими параметрами (mI, bP, bC) + одним статическим (bK), получаем модель только с одним динамическим параметром (mI) и двумя статическими (bK и коэф-т сглаживания). Фактически, теперь можно торговать все опционы (все страйки всех календарных серий на один БА) с помощью только одного параметра mI. Ну классно же?! :)



















Из улыбки можно получать распределение вероятностей — где будет БА на экспу. Возможно, для W-образной улыбки будет получаться распределение с двумя вершинами. С одной стороны — непривычно. С другой — почему бы и нет. Если, например, ожидается новость, после которой возможны только два сценария — либо точно вниз, либо точно наверх. А вероятность случайного блуждания у текущего уровня цены БА — минимальная. Тогда, по идее, возможна смесь двух распределений => два пика => улыбка с двумя донышками. Тут уже нужен сценарный подход. Модель Курбаковского так изогнуться не сможет. Если ее подгонять под такие цены, то она просто покажет, что по центру надо все продавать, а по бокам — выкупать. Т.е. как бы выправлять W в V или U.
Кстати парабола отвратительно калибруются к реальности, даже после трансформации к «правильным» координатам
Согласен, что торговать можно не только волой, и у распределения вероятностей есть не только второй момент (который и задает mI), но и третий/четвертый/… + различные сценарии. Да, все это многообразие одним параметром не поторгуешь. И если хочется сыграть на каких-то тонких моментах, то нужна будет другая модель (вернее, даже подход, например, поиск оптимальной позиции, когда споришь на уровне всего распределения). Но для простой торговли волой (вторым моментом распределения), мне кажется, модель Курбаковского подходит очень хорошо.
1. Цена — геометрическое броуновское движение. Это легко опровергается: составьте распределение приращений логарифмов цены и увидите, что там даже близко нет нормального распределения.
2. Торговля ведется непрерывно. А как же ночи, выходные, праздники?
3. Цена БА изменяется бесконечно малыми приращениями (чтобы можно было реплицировать опцион фьючом). Это тоже не так, бывают и скачки цены, и большие или даже огромные. А бывает, что сделку с фьючом можно совершить только через несколько планок. И финрез от действий с фьючом ну совсем не будет совпадать с финрезом от опциона.
И улыбка в моем понимании, это не нечто цельное, имеющее физический смысл, а просто набор поправочных коэф-тов. Химера :) Имхо, правильный взгляд на нее: смотрю на улыбку, а вижу множество логнормальных распределений (для каждого страйка), каждое из которых совсем не похоже на реальное рыночное. Подгонять модель 3-8-10 степени к этой химере, пытаться спрогнозировать, как будут меняться параметры такой модели при изменении БА, волы, времени — выглядит очень сомнительным, имхо.
1. После нормировки на локальную волатильность приращения логарифмов прекрасно вписываются в Гаусса кроме считанных исключений
2. Ну подмешайте jumps процесс. в чем проблема?
3. Примерно тоже самое что и 2
Физического смысла там и нет, есть экономический смысл закона спроса и предложения
wrmngr, добавляются лишние параметры, которые непонятно как фитить под реальную траекторию.
Есть рыночная улыбка, у неё 3 параметра — неплохо. Примерно понятно как они будут менятья во времени — вообще красота.
wrmngr, учитывая, что некоторые товарищи с известной долей презрения относятся к рыночной улыбке, попадать «всегда идеально» нам может быть и не нужно.
Тем более, что тут речь про акцию да ещё перед выходом какой-то корпоративной новости. Наверное, в такой ситуации такая форма улыбки имеет право считаться «безарбитражной». Не могу ничего сказать про Валинор. Там все злые и голодные бегают.
у вас есть такая модель? Я как-то думал про модель с тремя сценариями и там как раз 8 параметров получалось. Три сценария (падение, рост, и случайное блуждание на текущем уровне), под каждое свое нормальное распределение со своим весом (вероятность срабатывания сценария) + мю и сигма для каждого. Всего 9 параметров — 1 параметр мю центрального распределения (его матожидание равно текущей цене БА). Вот и получается 8 параметром. У вас, случаем, не такая модель?
Oliver Stocks, это самописная программа насколько понимаю.
Берете любимый редактор исходников, любимую компоненту для рисования графиков — и вперед.
Кузя, «ботаники» тоже разные бывают.
Вот и интересно было бы сравнить. Допустим, Вы торгуете 5 лет и имеете среднемесячную доху +2% с просадкой 20% от счета. На капитал 200 тыр.
Тогда Вы можете рассчитывать получить ответ сколько и на какой капитал зарабатывают опционщики со своими мат. моделями.
И это стратегия арбитража улыбки. Зиг заг. Поэтому мы имеем загиб улыбки. Случается, что он меняется и мы можем профит получать.
А вот цена… цена как повезет. Биды могут и несколько ш.ц. держаться почти до финального гудка.
Что за зверь? Гугл первой ссылкой выдает «Ядерная оценка плотности распределения». Если имеется ввиду работа через распределение вероятностей (где будет цена БА на экспу), то такое распределение у меня есть, но я же не знаю — с какой скоростью будут таять его хвосты?
Что касается доходности — у меня норма 30 годовых в валюте. У него, наверное, больше
Далее из коэффициентов bc,bp которые подбираются по рыночным ценам строится средневзвешенное b=bc*ac+bp*ap. Это гладкая функция страйка, на правом хвосте совпадает с bc, на левом — c bp. В центральной точке b=(bc+bp)/2. Этот сглаженный коэффициент используется для расчета цен опционов и всех производных. При этом кривая волатильности (мобильности) становится гладкой и принимает привычный вид.
Но, как я понимаю, это не единственный из возможных методов сглаживания.
А bk постоянно пересчитываете, или один раз прикинули и зафиксировали? Если не секрет, какие у Вас сейчас значения для Ri и Si?
Единственно, показалось странным, что иногда корреляция mH с приращениями цены была положительная. Т.е. БА наверх, и его вола/подвижность начинает расти. БА вниз — и вола падает. Как будто рынок не верит в рост, и когда фьюч растет — удивляется и начинает слегка бурлить туда-сюда. А когда Ri падает, то типа так и ожидалось, и сползание идет на минимальной воле. Вот это показалось странным: у bk отрицательный наклон, а у bh — положительный.