SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. Kot_Begemot
Критическая масса и критическое значение аналогичных стратегий
- 26 мая 2021, 04:03
- |
В первой части мы анализировали критический порог статистической значимости для сложных композитных систем на примере модели AR. В этот раз мы попытаемся быть чуть ближе к делу и проведем тесты для набора трендовых систем на базе Simple Moving Average. В качестве примера возьмем самый ликвидный фьючерс — белый шум, для которого заранее известно, что он абсолютно «не торгуемый» и попытаемся всё же что-нибудь под него подобрать из соображений трендовости «больших денег» и саморефлексии участников торгов.
Сгенерируем набор из 10 стратегий с периодом 10*i, i=1,2,...10.
Nstr=10;
x=randn(10000,1);
y=[x(2:end);0];
M=zeros(10000,Nstr);
for i=1:Nstr;
M(:,i)=tsmovavg(x,'s',10*i,1);
end;
M(1:Nstr*10,:)=0; R=M.*y; И оценим порог 70% статистической значимости коэффициента шарпа стратегии без учета размерности набора стратегий:
И с учетом размерности :
Эффективная размерность для набора из 10 SMA с различным периодом получилась 3.7368, что хорошо видно из корреляционной матрицы -
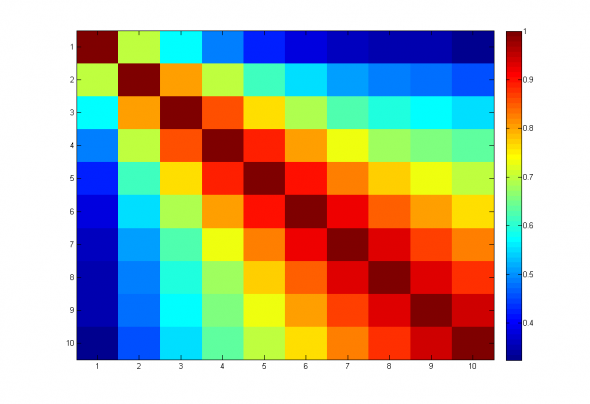
Рис 1. Корреляционная матрица набора трендовых стратегий с различным периодом.
Заметим, что для лучшего соответствия эмпирическим данным, мы заменили оценку эффективной размерности :
где Csqrt — матрица корней из корреляционных коэффициентов стратегий, так что обобщенное критическое значение получилось равным :
Изобразим полученные результаты тестов и полученные доверительные интервалы :
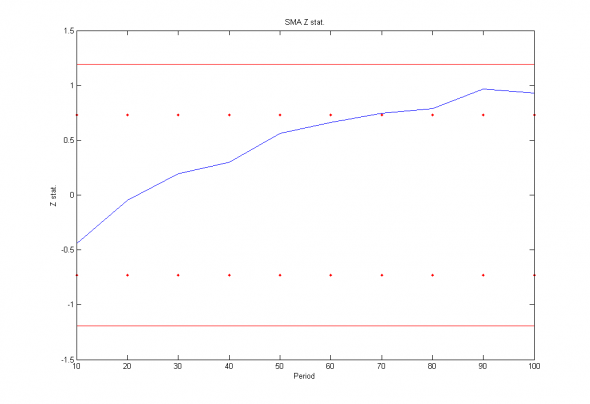
Рис 2. Z статистика для стратегий основанных на скользящих средних случайного блуждания в зависимости от периода (синяя линия), «классический» Z тест (красные точки) и модифицированный Z тест (красная линия).
Хорошо виден эффект слабой контрендовости в ближней зоне, связанный с влиянием «срочности» расчетов и «игрой по стопам» против трендового эффекта в дальней зоне, связанного с медленным переливанием «больших» капиталов. Тем не менее, даже не смотря на полное соответствие случайной реализации случайного блуждания с нашими глубоко профессиональными представлениями о рынке и на то, что сама совокупность стратегий образует достаточно широкое «облако антиподгона», с точки зрения статистики мы не можем утверждать, что способны обыграть случайное блуждание с вероятностью хотя бы 70%.
Что же, рассмотрим наши стратегии поближе -
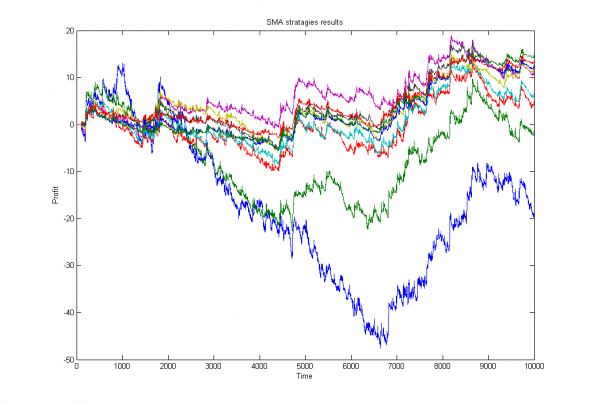
Рис 3. Изображение прибыли, полученной по различным стратегиям.
На первый взгляд ничего интересного, но из-за достаточно широкого «облака», характерного для данного класса стратегий (SMA), мы получаем возможность перескакивать с одного прибыльного тренда на другой и получать дополнительное преимущество от адаптации к изменяющимся неэффективностям рынка.
Проведем адаптативный run forward rolling active adaptation OOS тест (IS=600, oOS=300) на сетке параметров ( T=10*i,i=1,2,..10 ) :
K=600; Q=300;
IS=zeros(K,1);
Roos=zeros(10000,1);
for i=K:Q:10000-Q;
IS=x(i-K+1:i);
M=zeros(K,10);
y=[IS(2:end);0];
for j=1:10;
M(:,j)=tsmovavg(IS,'s',10*j,1).*y;
end;
M(1:100,:)=0;
sharp=mean(M)./std(M);
[a,per]=max(sharp);
if a>0;
Roos(i+1:i+100)=R(i+1:i+100,per);
end;
end;
plot(cumsum(Roos)); title('OOS test for SMA strategies at random noise'); xlabel('Time'); ylabel('Profit');И графически изобразим полученные результаты:
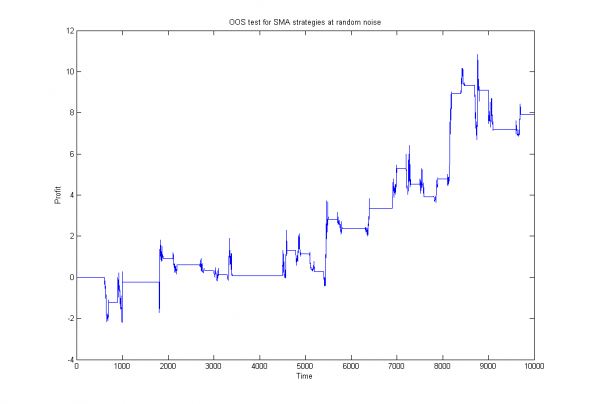
Рис 4. OOS тест для набора трендовых стратегий с переоптимизацией каждые 300 отсчетов на интервале 600 отсчетов.
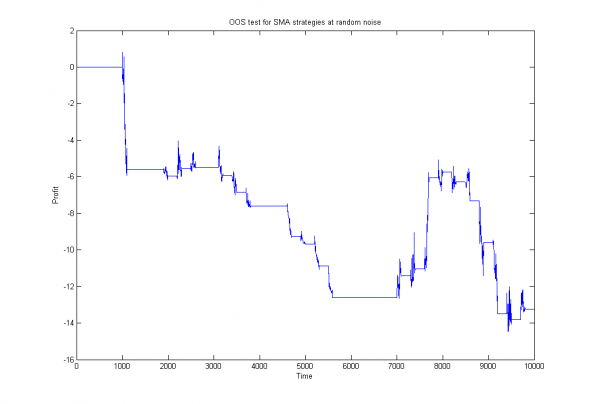
Рис 5. OOS тест для набора трендовых стратегий с переоптимизацией каждые 300 отсчетов на интервале 1000 отсчетов.
Что лишний раз подтверждает простую истину — закономерности случайного блуждания постоянно изменяются и прошлые закономерности быстро устаревают, поэтому оптимизировать портфель стратегий нужно как можно чаще и на как можно более поздних, ещё репрезентативных данных.
И какой из этого всего можно сделать вывод? А очень простой :
Что за новость, вот те на!
Пришла новая беда –
Дата-сайнс и Машин-лернинг
Применяют на ура!
Только лучше не спеши,
Сядь, подумай и реши.
Оверфитнуться здесь просто,
На бэктесты не греши.
Запросто она, цена,
Выйдет боком не туда
И утащит OOS тесты
За собою вникуда.
Замест чем опять гадать –
Где купить, а где продать?!
Взял бы лучше опционов,
Чтобы всё не проиграть!
Опционы это да –
Не случайная игра.
С ними можно спать спокойно!
…От утра и до утра.
Вон, смотри, как Старый Бес,
На какую гору влез!?
И в обчественном сознаньи
У него почет и вес!
Эту ж грамоту отложь,
Лишних сложностей не трожь.
Ежли не взлетишь как птица…,
То хотя бы доползешь.
теги блога Kot_Begemot
- API
- cpp
- FORTS
- LUA
- Matlab
- NASDAQ
- open source
- Quik Lua
- S&P
- S&P500
- S&P500 фьючерс
- Vanguard Group
- VIX
- акции
- акции США
- алгоритмы
- алготрейдинг
- анализ временных рядов
- баффет
- волатильность
- Гордон
- доверительное управление
- долги
- игры
- инвестиции
- индекc
- интеграция
- искусственный интеллект
- Келли
- Книги
- книги о трейдинге
- корреляция
- кризис
- криптовалюта
- лудомания
- Марковиц
- матлаб
- машинное обучение
- ММВБ Акции
- наука
- нейронные сети
- облигации
- одураченные случайностью
- оптимизация
- оптимизация торговых систем
- опционы
- оффтоп
- оционы
- памм счета инвестиции
- паника
- пирамида
- ПИФы
- портфели
- Портфель
- портфельное инвестирование
- пузыри
- раздача
- рецензия
- Риски
- рэнкинг мосбиржи
- Сбербанк
- спекуляции
- статистика
- стоимостное инвестирование
- талеб
- теги не нужны
- теория игр
- торговая система
- торговые роботы
- трейдинг
- улыбка волатильности
- управляющая компания
- финанализ
- фундаментальный анализ
- фьючерс ртс
- Шарп
- шутка
- Экономика



















Если брать скользяшки 99-101-102, то вроде бы 3 скользяшки, но с очень близкими результатами и если одной «повезет» заработать, то автоматом повезет и другим, поэтому доверительный интервал расширять не нужно. И наоборот, в случае скользяшек 10-1000-1000 000 мы получим 3 почти независимых стратегии, а это всё равно что взять три СВ, ни одна из которых не должна покинуть интервал. То есть для предельных случаев всё более-менее понятно.
А вот в промежуточных случаях надо что-то делать.
А как? Мы знаем, что дисперсия суммы зависимых стратегий (ед. дисперсии) = N^2, независимых — N
При этом дисперсия суммы изучаемого набора стратегий = l*C*l'
где l- единичный вектор, l' — его транспонирование, С — корреляционная матрица.
Тогда, чтобы ответить на вопрос сколько независимых СВ содержаться в нашем наборе, нам нужно составить ур-ие :
(a*N) + (1-a)^2*N^2 = l*C*l'
a*N+1 — число независимых компонент
(1-a)*N -1 — число идентичных компонент
в результате решения уравнения, получим, что :
Рановато я что-то начал забивать себе голову многомерными пространствами ))
Вы не ответили на вопрос:
А что делать, если никаким скользяшкам не повезет?
И никаким случайно выбранным нескользяшкам тоже?
Какие выводы следует делать в таком случае?
С уважением
С уважением
P.S. А если серьезно? Все модельные стратегии (комбинации МА) работают в минус. Все случайные стратегии (ну, которые мы смогли смоделировать) работают в минус. Что из этого следует?
Я не хотел критиковать Ваш интересный текст и загнать дискуссию в тупик
Но мне в самом деле интересно Ваше мнение )))
Представим себе, что мы не зарабатываем деньги на бирже, а просто ищем корни уравнения f(x)=0. Тут f может быть полиномом, может быть любой непрерывной функцией, в-общем, есть варианты.
И вдруг у нас ничего не получается. Метод Монте-Карло не находит ни одного корня. Moving Averages по прошлым испытаниям тоже не помогают. Полная засада! (про метод Ньютона мы не знаем, но MA не имеют к нему особого отношения, во всяком случае, не способны его заменить).
Вопрос?
Следует ли из наших безуспешных попыток найти корни уравнения, что у уравнения нет корней?
С уважением
А вдруг с точностью 10^(-5) корень есть, а c точностью 10^(-10) уже нет. В вычислительной математике и не то бывает.
Если f — полином степени N, то основная теорема алгебры гарантирует нам, что у него есть N корней. Не нашли ни одного — плохо ищем )))
С уважением
Хочется ответить что следует, но существуют ещё ограничения на функцию, гладкости, например и ограничения на корни. С другой стороны — а нужны ли нам такие корни и такие функции?
Если трудно найти ТС с хорошей эквити — это не значит, что ее нет )))
Или Вы таки сектант и считаете, что на любом рынке можно заработать всегда, в любой позе и в любое время суток?)
С уважением
Есть такая штука — корреляционный интеграл, который используется для оценки фрактальной размерности. Предположения о виде распределения не требуются.
но никому энто в теоретических целях и на фиг не надо… всем нужен за дешево относительно цены — качественный результат на уровне хорошо...
если просто так для души… поискать черную кошку в темной комнате при начальном условии, что ее тама отродяся не было… то энто интересно
Я уже второй год обещаю community написать развернутый пост про нелегкую жизнь на ниве лимитных ордеров, но руки так и не доходят. Мой косяк.
Зачем нужны лимитные ордера — думаю, вполне понятно.
1. Они позволяют достаточно строго контролировать косты при исполнении
2. Они дают в среднем значительно меньшие косты, чем маркетные ордера
Поэтому если Ваша система не супер-пупер-прибыльна, с маркетными ордерами и их проскальзыванием Вы далеко не уедете.
Итак:
1. Во вселенной лимитных ордеров системы, работающие в плюс — это редкость. С математической точки зрения — множество меры нуль в пространстве всех возможных стратегий.
2. Системы, основанные на МА, вообще не попадают в зону профита
Вопрос:
Что покажет Ваше моделирование при таких вводных?
С уважением
P.S. Я обозначил вполне реальную рыночную задачу, любое решение которой монетизируется. Так что это уже не чистая теория)
Вообще не понимаю — куда смотрит управление внешней разведки ФСБ?...
образованы, умеете рассказывать анекдоты, устойчивы к стрессам, печень запросто держит сильный алкогольный удар....
да и самое главное — еще и Спекуль на бирже....
Я еще и крестиком вышивать умею (это правда)
(густо краснеет...)
С уважением
потом по нему гадать на ромашке?...
поясните дальнейшие действия, если для Вас энто не составит затруднений…
Думаю, Александр Борисович имел в виду, что при отсутствии знаний о будущем (обычное случайное блуждание) системы Buy & Hold или Sell & Hold покажут наилучший результат в интервале.
На геометрическом случайном блуждании (логнормальное распределение) системы Buy & Hold или Sell & Hold являются оптимальными. Это было подробно доказано в одном из моих топиков.
Именно по этой причине на растущем тренде индексные инвесторы обогащаются и начинаю считать себя гениями )))
С уважением
спасибо, я понял, что хотел сказать А.Г… Ваши комментарии сделали картину — маслом еще более понятной и убедительной....
2. Какие основания полагать, что динамика цен на рынке как-то связана с белым шумом?
Белый шум предполагает горизонтальную АКФ (что встречается редко).
ТС скорее всего имел в виду нормальное распределение приращений цен.
С уважением
Спектральная плотность белого шума постоянна и не зависит от частоты.
Отсюда два очевидных следствия. Белый шум не ограничен ни во времени ни в делимости. То есть, физически невозможен.
1. Белый шум возможен для процессов с любым распределением вероятностей — равномерным, Коши, гипергеометрическим etc. Не думаю, что ТС имел это в виду
2. Физическая нереализуемость — это полная хрень
К примеру — процесс приращений цен актива имеет незатухающую АКФ — это физически невозможно. Однако, сей факт несложно проверить.
Если еще подробнее — нет никакой физической реализуемости. Есть лень математиков и физиков, которая превратила науку о бесконечных СЛАУ (систем линейных уравнений) в теорию ограниченных компактных операторов в гильбертовом пространстве. Ибо этот инструментарий рано появился и оказался вполне простым. Тем не менее, существуют и более глубокие факты о решениях бесконечных СЛАУ, но они не исчерпываются простым функциональным анализом в гильбертовых пространствах...
С уважением
Но искать надо там, где потерял, а не там, где зажег фонарик.
Если переходить к прикладной математике, любой Вам скажет, что ОЦЕНКИ коэффициентов корреляции плохо сходятся. Что для нестационарного процесса хорошо бы поискать другие методы описания. Иногда превосходно работает локальный переход к собственному базису (но это если он есть где-то рядом). Спектральное разложение в стиле SVD. Да хоть бы и бустинг.
Однако, мы можем попытаться строить АКФ постепенно
Начать с дневок...
Перейти на часовки...
Потом на минутки...
Потом на тики...
(дальше не было смысла)
Сама выборочная АКФ при этом будет куда-то сходиться (проверяется)
Однако быстро затухать на бесконечности не станет
Ни на каком таймфрейме
Так что «случайный» процесс приращений цен актива никогда не станет «физическим» процессом. А так и останется процессом с бесконечной энергией. Как белый шум и прочие странные придумки...
С уважением
Если Вы возьмете более-менее макроуровень, Вы увидите, что взятая как функция времени оценка некоторого к-та автокорреляции по ограниченному окну (скользящему во времени) нестационарна. Какая уж тут сходимость. Как в анеке про военку.
— Товарищ майор, у Вас написан предел синуса на бесконечности равным 0. Но синус не сходится на бесконечности.
— Товарищ студент, Вы не поняли, эта формула для военного времени.
А если я возьму микроуровень — то увижу, что эта оценка стационарна
(просто Вы этого не делали)
Поэтому и писал в наших с Вами дискуссиях, что не верю в стационарность рыночных процессов, но верю в их эргодичность.
С уважением
Тики на неликвиде прямо таки вопиют о стационарности и эргодичности.
И Ваши методы, и методы А.Г., и мои имеют ограниченную область применимости, мы часто абсолютизируем свои выводы, не оговаривая ограничений. И рискуем впасть в аллегорию про слепых и слона.
Просто на микроуровне все устроено просто, а на макро — сложно.
И я не верю (пока), что начав с макроуровня, можно построить богатую непротиворечивую теорию.
С уважаемым А. Г. мы вообще непохожи, но спасибо за сравнение — мне это лестно )))
Я не оперирую неликвидом, для меня основной рынок — это FX, т.к. больше практически нигде нельзя мгновенно перевернуть позу на несколько десятков миллионов долларов. И да, тики на FX просто вопиют об эргодичности (я ничего не утверждал про стационарность).
Ну а если все исследования рынков основывать на котировках болота под названием MOEX, то в итоге можно накропать только диссертацию о свойствах болота. Может и существенных. Но мне это неинтересно. Ничего личного. И без обид, плз.
С уважением
Синус на бесконечности таки сходится к нулю )))
По Эйлеру, по Чезаре и даже по Борелю (вроде бы) )))
С уважением
Но просто lim Sin(x) при Х стремящемся к бесконечности не существует.
Точно также, при минимальном изменении аксиом математики, непрерывная функция, которая выше нуля в начале отрезка и ниже 0 в конце не обязательно имеет значение равное 0 внутри отрезка. Хотя обратное доказывают на 1 курсе универа.
Я неплохо владею и традиционным анализом, и нестандартным (по Робинсону).
Не хотел смутить Вас ))) Просто ссылка на сходимость по Эйлеру/Борелю была не вполне шуткой. Именно так и удается решать бесконечномерные СЛАУ, которые неразрешимы с точки зрения методов Великого Давида Гильберта. Традиционные методы тупо расходятся (отсутствует регулярность).
С уважением
P.S. Вы, кстати, никак не прокомментировали феномен сходимости коэффициентов корреляции на микроуровне. Этот уровень практически н не знает ни праздников, ни ночных гэпов…
Ачипятка
АКФ белого шума — это дельта-функция
Однако на распределение приращений это никакого влияния не оказывает
С уважением
Страхуюсь от иллюзии найти то, чего нет и, что не мало важно, много на это поставить.
Белый шум — это процесс с равномерной спектральной плотностью
Распределение приращений при этом может быть любым — нормальным, равномерным, Коши, экзотическим etc.
Могу на бис попробовать придумать тип (сильно смещенного) приращения, при котором результат торговли не будет абсолютно случайным в Ваших терминах )))
С уважением
Если бы я знал как решить задачу точно, то я бы написал, но пока у меня только приближенная оценка исходя из того, что в граничных условиях (корреляция = 0 и корреляция=1) решение нам точно известно. Дальше вопрос провести между ними некоторую гладкую функцию. Желательно при этом более-менее точно.
Может быть, если позже придет решение, опишу.
Если Вы о корреляции скользяшек между собой, то она, естественно есть, по построению. Если Вы нашли существенные отклонения АКФ исходных данных, проверьте датчик случайных чисел. Возможно, у Вас шум спектрально окрашен, например, подчеркнуты низкие частоты.
это очень смелое утверждение и возможно не верное в корне.
Можно легко найти зависимость между ростом цен на картошку со вчера на сегодня и ростом цен на картошку с сегодня на завтра.
Проверяется на 100% активов.
Писал подробно в своем блоге.
Торговать в плюс не позволяет.
Но все равно крайне интересно)
С уважением
а это вот ключевое. если есть то путь в миллионам. а если нет, ну не повезло )))
Я подробно писал в своем топике что (на тиковом или минутном таймфреме) все активы делятся на 2 категории
1. LP (если предыдущую минуту росло — будет расти и следующую)
2. LA (если предыдущую минуту росло — следующую будет падать)
Работает всегда и везде. Исключений (3-й категории) нет. Проверяется элементарно в Excel. К какому из классов относится конкретно картошка — лично мне фиолетово...
С уважением
P.S. Денег в этом факте не закопано. Но сама закономерность доставляет)
Но это еще один камень в огород сторонников случайного изменения цен)
С уважением