SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. Toddler
Физико-математические основы Грааля. Часть 13. И вновь о случайном блуждании...
- 29 мая 2021, 13:00
- |
Время от времени, на разных форумах, то и дело вспыхивают ожесточенные споры: можно или нет заработать на случайном блуждании?
В этих спорах есть все: ярость и гнев, боль и отчаяние, знания и домыслы, ссылки на научную литературу, смех и слезы… Короче — все, кроме Истины...
Главенствует идея, что на СБ заработать невозможно. А раз так, то надо искать отличия рыночного ряда от СБ и на этих отличиях получать профит.
А ведь еще Колдун говорил: «Трейдер только тогда начнет зарабатывать на рынке, когда поймет, что заработать на случайном блуждании — легче легкого».
Нет. Не слушают Колдуна… Преданы забвению Древние Истины...
Дошло до того, что один из страждущих, потратив немало времени на создание генератора равномерно распределенных случайных чисел, создал интегрированный ряд этих чисел и предложил мне показать свое мастерство.
Вот этот ряд: https://disk.yandex.ru/d/QV5HEU5TyPgUrQ
Что можно сказать? Отличный, классный генератор. Сложный ряд.
Абсолютно независимые приращения, которые на фазовой плоскости дают следующую картину зависимости текущего приращения от предыдущего:
Интегрированный ряд выглядит так:
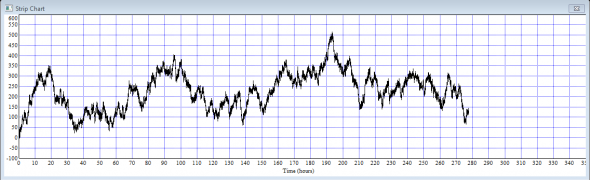
Итак, мне было предложено заработать на этом ряде.
А я чё? Я — ничё… И при чём здесь именно я? Ведь я — всего лишь Его Тень...
Берем за основу метОду, изложенную здесь: https://smart-lab.ru/blog/579572.php, которая основана на теореме Ляпунова о том, что набор сумм независимых или слабозависимых величин, образует нормальное распределение.
Выборка для скользящего окна — 7200 значений.
Дисперсию суммы приращений (Cusum) в скользящем окне определяем как:
D=S^2=(Sigma^2)*N,
где Sigma — среднеквадратическое отклонение распределения приращений в скользящем окне, N=7200 — размер скользящего окна.
Т.о. стандартное отклонение процесса изменения значения суммы приращений
S=Sigma*sqrt(N)
При выходе Cusum за границу +2.5758*S, заключаем сделку SELL, а за -2.5758*S, соответственно, сделку BUY. Выход из сделки — при возврате Cusum к 0.
Смотрим:
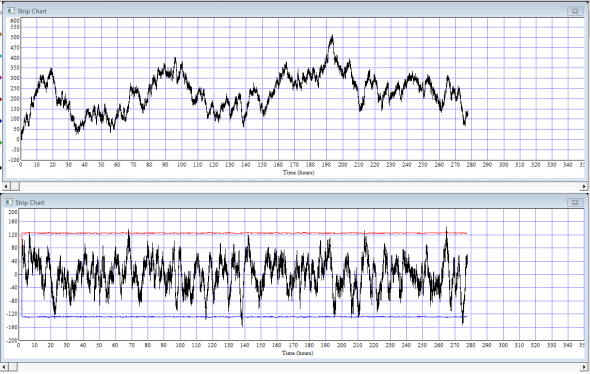
На нижнем графике — процесс изменения Cusum в заданных границах. И хотя входы/выходы производятся по нижнему графику, сами сделки, естественно, заключаются по значениям верхнего графика. Того самого, на котором мне было предложено заработать...
Итог:

Проведено 10 сделок (+8/-2) с общим профитом +172.56.
Никаких проблем...
Заработать на случайном блуждании, действительно, легче легкого.
А на рынке это работает??? А как?.. А зачем и почему?.. А дальше-то что???
Хе-хе...
А дальше — Бездна.
Toddler.
В этих спорах есть все: ярость и гнев, боль и отчаяние, знания и домыслы, ссылки на научную литературу, смех и слезы… Короче — все, кроме Истины...
Главенствует идея, что на СБ заработать невозможно. А раз так, то надо искать отличия рыночного ряда от СБ и на этих отличиях получать профит.
А ведь еще Колдун говорил: «Трейдер только тогда начнет зарабатывать на рынке, когда поймет, что заработать на случайном блуждании — легче легкого».
Нет. Не слушают Колдуна… Преданы забвению Древние Истины...
Дошло до того, что один из страждущих, потратив немало времени на создание генератора равномерно распределенных случайных чисел, создал интегрированный ряд этих чисел и предложил мне показать свое мастерство.
Вот этот ряд: https://disk.yandex.ru/d/QV5HEU5TyPgUrQ
Что можно сказать? Отличный, классный генератор. Сложный ряд.
Абсолютно независимые приращения, которые на фазовой плоскости дают следующую картину зависимости текущего приращения от предыдущего:

Интегрированный ряд выглядит так:

Итак, мне было предложено заработать на этом ряде.
А я чё? Я — ничё… И при чём здесь именно я? Ведь я — всего лишь Его Тень...
Берем за основу метОду, изложенную здесь: https://smart-lab.ru/blog/579572.php, которая основана на теореме Ляпунова о том, что набор сумм независимых или слабозависимых величин, образует нормальное распределение.
Выборка для скользящего окна — 7200 значений.
Дисперсию суммы приращений (Cusum) в скользящем окне определяем как:
D=S^2=(Sigma^2)*N,
где Sigma — среднеквадратическое отклонение распределения приращений в скользящем окне, N=7200 — размер скользящего окна.
Т.о. стандартное отклонение процесса изменения значения суммы приращений
S=Sigma*sqrt(N)
При выходе Cusum за границу +2.5758*S, заключаем сделку SELL, а за -2.5758*S, соответственно, сделку BUY. Выход из сделки — при возврате Cusum к 0.
Смотрим:

На нижнем графике — процесс изменения Cusum в заданных границах. И хотя входы/выходы производятся по нижнему графику, сами сделки, естественно, заключаются по значениям верхнего графика. Того самого, на котором мне было предложено заработать...
Итог:

Проведено 10 сделок (+8/-2) с общим профитом +172.56.
Никаких проблем...
Заработать на случайном блуждании, действительно, легче легкого.
А на рынке это работает??? А как?.. А зачем и почему?.. А дальше-то что???
Хе-хе...
А дальше — Бездна.
Toddler.



















Результат одинаков и строго положителен. Поэтому — метод работает, пока не доказано обратное.
Теория вероятностей говорит, что заработок на СБ является случайной величиной, проверяем…
Взял исходный файл, откалибровал параметры, сгенерировал 1000 траекторий, протестировал согласно предложенной модели…
Результаты:
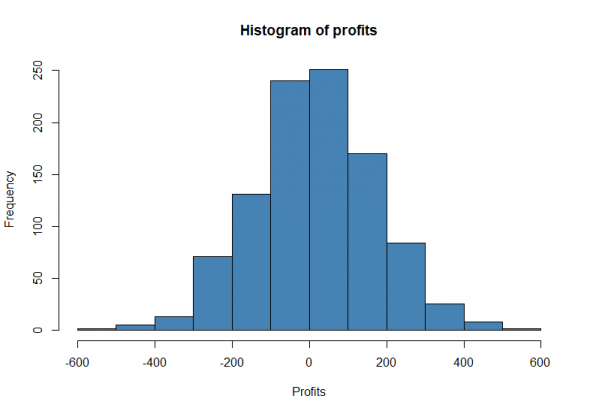
Shapiro-Wilk normality test: p-value = 0.9151 т.е. распределение полученных результатов прибыльности существенно не отличается от нормального
Выводы:
На СБ можно равно вероятно как заработать так и потерять, согласно ЦПТ в пределе прибыль стремится к нулю
Честно говоря, неожиданный для меня результат, но я склонен грешить, что я чего-то делаю не то. Надо будет все перепроверить, взяв умные книги)))
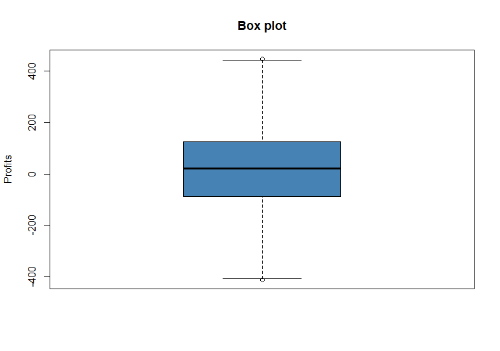
Итак, к результатам:
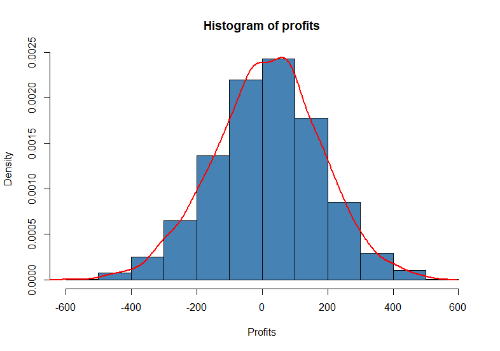
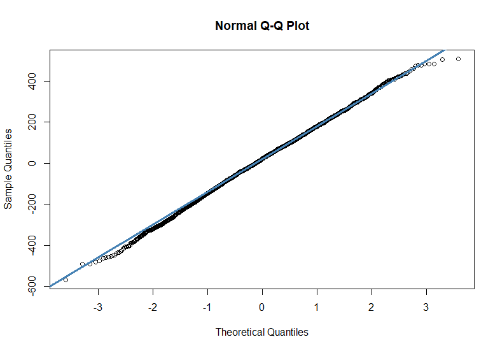
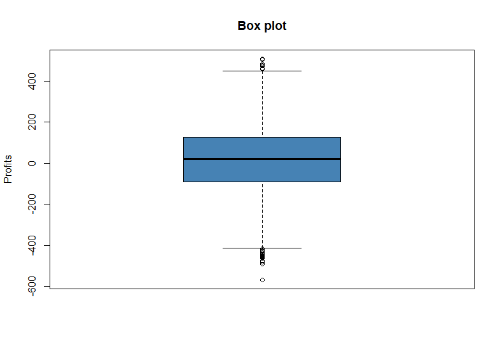
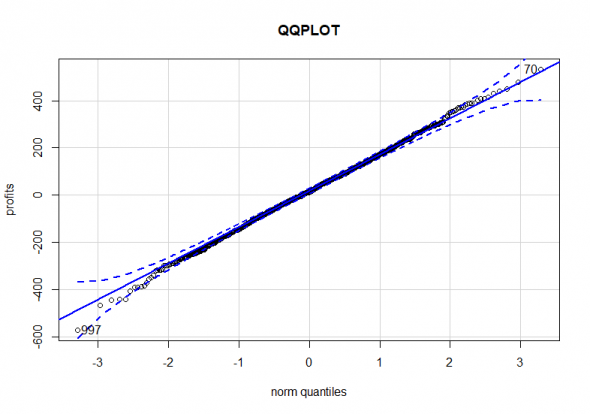
Начинаем с оценки распределения выигрышей и проигрышей на нормальность, смотрим визуально
что-то похожее на нормальное.
Тесты:
Shapiro-Wilk normality test
W = 0.99894, p-value = 0.06206
Anderson-Darling normality test
A = 0.78803, p-value = 0.04098
при 5-% уровне значимости… ну-у-у почти нормальное
при 1-% — отвергаем нулевую гипотезу о нормальности
Далее интересней)
Одновыборочный Т-тест на равенство выборочного среднего нулю:
One Sample t-test
t = 5.5464, df = 2999, p-value = 3.17e-08
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
10.74520 22.49687
sample estimates:
mean of x
16.62104
Итак, гипотезу о средней прибыли равной нулю можно смело отвергать даже при однопроцентном уровне значимости.
Теперь все тоже самое после удаления выбросов из результатов.
Shapiro-Wilk normality test
W = 0.99781, p-value = 0.0003555
Anderson-Darling normality test
A = 0.70627, p-value = 0.06521
One Sample t-test
t = 6.1144, df = 2972, p-value = 1.096e-09
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
12.08241 23.48974
sample estimates:
mean of x
17.78607
Как видим с нормальностью распределения все так-же не однозначно, но данные о среднем подтверждаются еще более убедительно.
Какой вывод? Надо перепроверить и усиленно думать)))
Идея то автора очень проста. Я бы ее перефразировал по другому. Если кому либо удастся преобразовать нестационарный случайный процесс в стационарный, то вероятность заработка на этом повышается.
Если выкинуть все эмоции из описания, то сухой остаток будет следующим. Автор пытается составить портфель из набора финансовых инструментов на бирже, и потом преобразовать его в какой — то стационарный случайный процесс. Алгоритм дальше просто - выше стандартного отклонения — продаем, ниже — покупаем.
Если действительно ему это удалось, то заработать на этом скорее всего можно.
Какой автор берет портфель , как он его преобразовывает, автор не конкретизирует. Но наверное это его ноу — хау.
Но к «случайному блужданию» это все не имеет абсолютно никакого отношения просто по опеределению случайного блуждания, и из случайных блужданий (скольких угодно) нельзя составить стационарный процесс.
У теоретиков этой странной теории о случайном блуждании есть такие постулаты: «Цены не имеют памяти», и «Сегодняшняя цена на актив не имеет ни какого отношения ко вчерашней цене на актив». Но цены-то обязаны своим появлением решениям, которые принимают люди, заключая биржевые сделки. А у людей есть-таки память. И они помнят какой была цена на актив вчера, и делают предположения о причинах, повлиявших на движение цены в предыдущую торговую сессию. И если у людей есть уверенность в том, что факторы, толкнувшие цену актива вверх или вниз, сохраняют свою силу, они поддержат зародившийся тренд, придав ему дополнительную силу.
Я сам не трейдер, а долгосрочный стоимостной инвестор, но я полагаю, что разговоры про трендовые спекулятивные стратегии имеют больше смысла, чем разговоры о возможности заработать на случайных блужданиях.
да это не трейдер, это кодер с форума MQL. Там уже коллеги ссаными тряпками погнали его из комьюнити за многолетнюю пургу. Теперь будет здесь изливать, благо свободных ушей здесь с избытком.
если вы даже не кодер, тогда я не знаю, что вы делаете в том комьюнити, впрочем, как и в этом :)
И поэтому я не могу давать оценку тому, чего не понимаю.
Buy&Hold
Sell&Hold
Cash&Hold
А я с этим и не спорил. То есть как раз написал, что рассуждать о зарабатывании денег на случайном блуждании — бред по определению случайного блуждания.
у нас, как понимаю, только и есть, что процесс случайного блуждание… так что зарабатывать больше по определению и не на чем....
"Что делать, Фауст? ..."©
отметать сходу «фантастические идеи" Todlera тоже не очень хочется…
что то подобное я использую в качестве верхнего и нижнего маркера, когда спрыгивать с тренда и когда снова на него запрыгивать...( типа выполняю комплекс спортивных упражнений...
Если мы про случайное блуждание — разумеется, никакие шаманские методы ничего не дают для его предсказания, поэтому «фантастически идеи» молокососа — они именно что от непонимания происходящего. Всякий теханализ работает именно потому, что цены — не случайное блуждание.
далее приставать не буду… так как энта тема — Вечная Тема на смарте… и каждый понимает ее по своему…
спасибо, что откликнулися…
СБ легко «преобразуется» в стационарный процесс путем процедуры взятия разности: DZt =Zt — Zt-1 = et Автор называет это стационарностью приращений, и как я понимаю, использует ЦПТ для частичной суммы СВ et ~ iid(0, s2) Идея только в этом? Есть ли здесь аналогия с подбрасыванием монетки, и принятии решения ставить на решку, если выпало 10 орлов подряд, и наоборот? Точнее, ставить на то, что в следующих нескольких бросаниях выпадет достаточно решек, чтобы нивелировать сильное отклонение, вызванное серией орлов?
А стоит всего лишь:
1. Продлить набор данных (подбрасывать монетку дальше)
2. Обновить набор данных (заново 5 раз подбросить монету)
И как туман рассеется эта ваша «стратегия».
Я искренне рад за вас, если все получилось.
Здравствуйте,
чем отличается марковский от немарковского процесса?
в чем суть разницы?
т.е. Саймонс ошибается?
smart-lab.ru/blog/394251.php