Блог им. TradeTab
Кредит увеличивает риск портфеля?
- 08 июля 2022, 17:02
- |
Ниже представлены сделанные в недавнем прошлом расчеты, они не учитывают примерно 1,5 последних года рыночных данных, но это не существенно, поскольку на общие выводы это не повлияет.
Мне нужно было рассчитать оптимальные веса бумаг в портфеле, чтобы он считался эффективным согласно портфельной теории Марковица.
Для этого была построена ковариационная матрица анализируемых акций:
Далее была рассчитана ожидаемая доходность и стандартное отклонения портфеля:
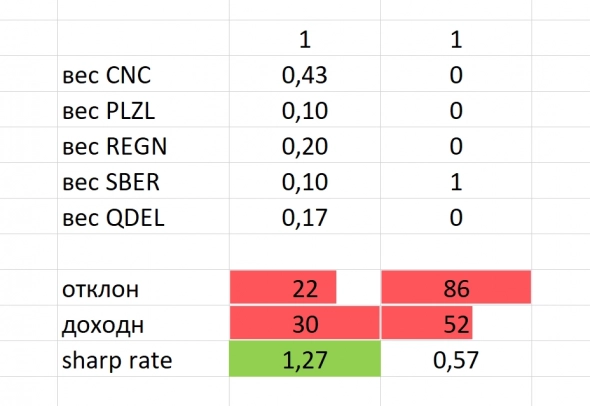
В левом столбце показано эффективное распределение весов акций в портфеле, при котором коэффициент Шарпа имеет максимальное значение, то есть то, при котором портфель имеет максимальную ожидаемую доходность с наименьшим риском.
В столбце справа веса распределены так, чтобы портфель обеспечил максимально возможную ожидаемую доходность с любым риском. Как видно, для этого необходимо инвестировать все средства в SBER. При такой ожидаемой доходности стандартное отклонение, то есть риск портфеля, крайне высоко и означает, что с вероятностью 95% реальная доходность окажется в диапазоне от -120 до +224, в случае с акциями нижняя граница будет ограничена -100, но предполагаемый диапазон все равно слишком широк.
Теперь посмотрим, что произойдет, если воспользоваться кредитом.
Возьмем наш эффективный портфель из левого столбца и добавим к нему 100%-ое заемное финансирование по ставке 15%, ожидаемая доходность и стандартное отклонения рассчитывается так:
r = (2 * ожидаемая доходность портфеля) – (1 * процентная ставка)
сигма = (2 * сигма портфеля) – (1 * сигма кредита)

В результате ожидаемая доходность портфеля почти равна ожидаемой доходности вложения в самую рисковую акцию портфеля, но при этом стандартное отклонение снижается вдвое, что делает наши ожидания более надёжными, а риск портфеля ниже. Достигается это за счет того, что кредит имеет нулевую сигму.
Вывод прост: если наша цель получить максимальный доход из заданного набора акций, мы обязаны использовать заемное финансирование, которое, вопреки интуитивным ожиданиям, не увеличивает, а снижает риск портфеля.




















Ну и плюс явно некорректно учитывать сигму кредита, это не актив. Актив — это акции, купленные на кредит, у них совершенно не нулевая сигма.
Если мы говорим о том, какой портфель эффективнее, то конечно мы должны сравнивать портфель с плечом и портфель без плеча, с одинаковым весовым распределением акций в них. И в таком случае портфель без плеча будет привлекательнее, о чем и говорит коэффициент Шарпа.
Но здесь речь о том, что если мы хотим получить максимально возможный ожидаемый доход из рассматриваемых акций, то мы можем либо купить SBER, либо собрать эффективный портфель, но с плечом. В таком случае ожидаемые доходности будут почти идентичны, но риск будет в два раза ниже.
Если ставка кредита не меняется на всем сроке кредитования и в договоре не прописано условий, при достижении которых ставка увеличивается или уменьшается, то сигма кредита равна нулю.
А тот факт, что за кредит приобретаются активы имеющие ненулевую сигму отражается как 2 * на сигму портфеля, подразумевая, что начальная сигма портфеля увеличивается на 100% за счёт кредита
1. Риск портфеля считают на основе риска его активов
2. Кредит не является активом, только если это не кредит, выданный вами
Иначе у вас будет получаться, что с ростом займа ваши риски падают, но на самом деле будут расти вплоть до катастрофических размеров. Плюс если у Сбера наивысшая ожидаемая доходность, ну посчитайте ее, если купите Сбер в кредит.
Владимир,
1. «риск портфеля считают на основе риска его активов» – верно. Поэтому сигма портфеля умножается на 2, если бы мы брали кредит в размере 200%, а не 100%, мы бы сигму портфеля умножали на 3 и т.д. Как итог: по мере роста займа – растет и риск портфеля.
2. «кредит не является активом» – верно, это пассив, наши обязательства, поэтому мы его вычитаем из общей сигмы портфеля. Но кредит имеет нулевую сигму и он не оказывает влияния на портфель.
Если бы кредит имел сигму отличную от нуля – это означало бы, что имеется положительная вероятность изменения стоимости кредита в большую или меньшую сторону, для нас это значило бы, что имеется некоторый шанс заплатить за предоставленный нам кредит меньше, чем ожидается – для нас это выгода, которая частично компенсирует риск портфеля. Сигма портфеля – наш риск, сигма кредита – риск банка, или наша потенциальная выгода, потому второе вычитается из первого. Если бы мы не взяли кредит, а предоставили его кому-нибудь, то тогда мы должны были бы суммировать риск портфеля и риск кредита.
Но, повторюсь, сигма стоимости кредита почти во всех ситуациях нулевая, потому её можно вообще не рассматривать.
3. Да, можно взять SBER с кредитом, но основной смысл, который я хочу передать, в том, что комбинацией эффективного портфеля и кредита можно достигнуть любой доходности, но с меньшим риском. Допустим, чтобы получить доходность равную комбинации SBER + кредит, нужна комбинация эффективный портфель + (кредит*2), получится тоже самое, о чем и велась речь в посте: доходность будет примерно таже, но риск ниже.
Доходности прошлых периодов не гарантируют доходности в будущем. Так что просадка может быть больше, а плече сделает её недопустимо большой.
Если честно я с этой матрицей заманался подбирать акции, если у тебя есть еще пара лет статистики для форвард теста. На них все переворачивается.
В выводе говорится «если наша цель получить максимальный доход из заданного набора акций», то есть повествование в посте ведётся о получении не эффективной, а максимально возможной доходности.
Мы определяем при какой структуре портфель имеет максимальную доходность, а затем понимаем, что кредит позволит достигнуть этого значения с меньшим риском.